Слайдовая атака. 
Криптографическая защита информации: симметричное шифрование

С ростом скорости современных компьютеров, скоростные алгоритмы шифрования используют все больше и больше раундов, признавая все существующие криптоаналитические технологии бесполезными. Это, главным образом, происходит из-за того, что такие популярные методы, как линейный и дифференциальный криптоанализ, являются статистическими атаками, превосходными при статистических непостоянствах.

Однако, когда алгоритм шифрования имеет большое количество раундов, каждый добавленный раунд требует экспоненциального роста усилий атакующего.

Стремление к большому числу раундов можно наглядно увидеть, рассмотрев претендентов на конкурс AES. Несмотря на то, что одним из основных критериев для претендентов была скорость, некоторые представленные кандидаты (при этом не самые медленные) имели действительно большое число раундов: RC6(20), MARS (32), SERPENT (32), CAST (48). Это является следствием того, что после некоторого большого числа раундов даже относительно слабый шифр становится стойким. Например, алгоритм шифрования DES, уже взлом шестнадцати раундов представляет трудную задачу, не говоря о 32 и 48 раундах (двойном и тройном алгоритме DES). Таким образом, для криптоаналитика становится естественным поиск новых методов анализа, не зависящих от числа раундов в алгоритме шифрования.

В этом подразделе мы рассмотрим новый метод криптоанализа, нс зависящий от числа раундов в алгоритме шифрования, который называется «слайдовой атакой» или «скользящей атакой» (Slide Attacks), предложенный в 1999 г. А. Бирюковым и Д. Вагнером [27]. Этот метод применим ко всем алгоритмам блочного шифрования.

В то время как два других метода криптоанализа, таких как линейный и дифференциальный, концентрируются главным образом на распространенных свойствах техники шифрования, слайдовая атака использует степень самоподобия, что является принципиальным отличием. Под самоподобием понимается использование одной и той же криптографической F-функции, зависящей от одного и того же подключа, в каждом раунде шифрования. В зависимости от структуры алгоритма шифрования слайдовая атака может использовать как слабость процедуры формирования подключей, так и более общие структурные свойства шифра. Самый простой вид этой атаки обычно легко пресечь, избавившись от самоподобия в алгоритме шифрования. Более сложные варианты этой атаки имеют более сложный анализ, и против них гораздо труднее защититься.

Самый простой вариант слайдовой атаки рассчитан на анализ алгоритмов шифрования, состоящих из г раундов, каждый из которых содержит в себе F-функцию, зависящую от одного и того же значения ключа К. Такой тип алгоритмов шифрования называется гомогенным. К гомогенным также относятся алгоритмы, в которых функция формирования подключа периодична, т. е. один и тот же подключ извлекается через равное количество раундов. Говоря математическим языком, Fj = Fj для всех i=jmodp, где р является периодом. В самом простом случае р=1, и в каждом раунде используется один и тот же подключ.

При рассмотрении слайдовых атак, с целью упрощения мы будем рассматривать алгоритмы шифрования, в которых сложение шифруемых данных с подключом происходит непосредственно перед F-функцией. Так, если мы рассматриваем алгоритм шифрования, построенный по схеме Фейстеля, на вход которого поступает n-битное сообщение, то длина подключа будет составлять п/2 битов.

На рис. 104 показан процесс зашифрования n-битового открытого текста Х₍₎, в результате которого получается шифртекст Х_г. Здесь Х| обозначает промежуточное значение данных после j-ro раунда зашифрования, так что.

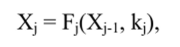
где j = 1, 2, 3, …, г. В дальнейшем мы иногда будем опускать значение к в обозначении F-функций и будем писать F (x) или F,(x) вместо F (x, k) или Fj (x, k).

Рис. 104. Схема обычного блочного алгоритма шифрования.

Функция F называется слабой в том случае, если при известных двух равенствах F (xl, k) = yl и F (x2,k) = у2 ключ к легко определяется. На рис. 105 показано, как может быть применена слайдовая атака к алгоритмам шифрования такого типа.

Рис. 105. Схема обычной слайдовой атаки.

Идея заключается в том, что можно сопоставить один процесс зашифрования с другим таким образом, что один из процессов будет «отставать» от другого на один раунд.

Пусть Х₀ и Х₀' обозначают исходные открытые тексты, Xj = Fj (Xj-i) и Xj' = Fj (Xj.i'), где] = 1, 2, 3, …, г. Идея заключается в том, что если мы имеем такую пару значений, что X) = Х₀ то мы также будем иметь соответствующую им пару значений, такую что X_r = X_r_t'. Предположим, что Xj = Xj_i тогда мы можем сказать, что Xj_+] = F (Xj) = F (Xj.i') = Xj'. Пара открытых текстов и соответствующих им шифр-текстов (Р, С), (Р', С') называется слайдовой парой в том случае, если F (P) = Р' и F© = С'.

Слайдовая атака проходит следующим образом. Мы получаем 2"' пар открытый — закрытый текст (Р, Cj), и ищем среди них слайдовые пары. Согласно парадоксу дней рождений, мы ожидаем найти хотя бы одну пару индексов i, i', такую, что F (Pj) = Р;' и F (Cj) = Q' одновременно выполняются для некоторого ключа. После того как слайдовая пара найдена, мы можем найти некоторые биты подключа. В том случае, если раундовая функция слабая, мы можем найти весь подключ данного раунда. Для нахождения оставшихся битов секретного ключа необходимо определить следующую слайдовую пару, и с ее помощью провести анализ. Таким образом, достаточно найти всего несколько слайдовых пар для полного определения битов секретного ключа, что и является задачей, стоящей перед криптоаналитиком.

В случае, когда речь идет об алгоритмах шифрования, построенных по схеме Фейстеля, раундовая функция F ((l, r), к) = ((l (c)f®, r), к) модифицирует только половину входного сообщения. Таким образом, условие F (x) = х' можно легко проверить с помощью сравнения левой части сообщения х и правой части сообщения х Это условие позволяет нам снизить сложность атаки на основе известных открытых текстов до 2″ ² известных текстов. У нас есть n-битовое условие нахождения потенциальной слайдовой пары: если (Pi, Q) образует слайдовую пару вместе с (Pj', Cj'), то тогда F (Pj) = Pj' и F (Q) = С/. Для нахождения слайдовой пары для алгоритмов шифрования, построенных по схеме Фейстеля, необходимо известные тексты (Pj, Cj) занести в таблицу, после чего для каждого j найти такой текст, чтобы правые половины Pj и Cj' были равны левым половинам Pj' и Cj.

Если не все биты подключа будут найдены с помощью определенной слайдовой пары, то можно будет использовать другие слайдовые пары для определения оставшихся битов.

Для алгоритмов шифрования, построенных по схеме Фейстеля, сложность анализа может быть снижена до 2″ ⁴ текстов в том случае, если существует возможность использовать выбранные открытые тексты. Для этого необходимо выбрать произвольным образом п/2 битовое значение х. После этого надо подобрать массив из 2″ ⁴ открытых текстов Pj = (х, у,), которые будут отличаться только случайно выбранной правой частью, и массив из 2″ ⁴ текстов Pj' = (у,', х), которые будут отличаться только случайно выбранной левой частью. Таким образом, у нас появится 2^w2 пар открытых текстов, и мы надеемся найти среди них хотя бы одну правильную пару.

В любом из вышерассмотренных случаев поиск слайдовых пар является вычислительно сложной задачей, для решения которой целесообразно использовать параллельные алгоритмы.