Многомерное интегрирование. 
Численные методы. 
Основы научных вычислений

При переходе от задачи вычисления одномерных интегралов к многомерному интегрированию возникает целый ряд новых проблем. В одномерном случае мы имеем три возможных типа области интегрирования: конечный, полубесконечный и бесконечный интервалы. В многомерном случае мы сталкиваемся с большим разнообразием областей интегрирования. В дополнение, подинтегральная функция может иметь особенность не только в точке, а также во множествах точек, таких как, например, интервал, плоскость и т. д. Поэтому вычисление многомерных интегралов представляет собой значительно более сложную задачу по сравнению с одномерным случаем.

Для таких областей, как квадрат, куб, цилиндр и т. д., которые представляют собой декартовые произведения областей более низкой размерности, можно построить формулы интегрирования, «перемножая» формулы для вычисления интегралов более низкой размерности (правило перемножения). Так, если.

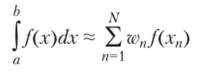
есть одномерная формула интегрирования, то.

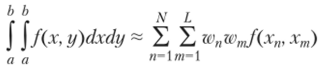
дает формулу для вычисления двумерного интеграла. Однако такие методы не всегда самые эффективные. В этом параграфе мы рассмотрим более универсальный подход к вычислению многомерных интегралов, который, в частности, включает в себя и правило перемножения.

Вначале рассмотрим интегрирование по квадратной области S= {-1 < г < 1,-1 < s < 1}на плоскости, и наша задача — построить кубатурную формулу для вычисления интеграла.

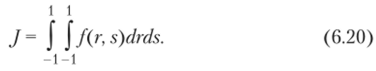
Введем некоторые узлы (г_ь л,), (r₂, s₂), •••> 0/,> ^si.) и соответствующие веса W,…, т&1 таким образом, чтобы формула.

была точной для одночленов вида г"У", п > 0, т > 0, как можно более высокой степени п + т < р. Для простоты мы рассмотрим случай L = 4 (рис. 6.5).

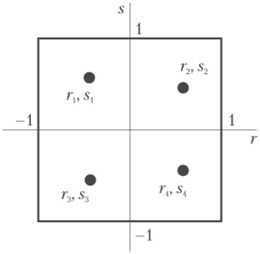
Рис. 6.5. Расположение узлов кубатурной формулы (6.21) в случае L = 4.

Подставляя функцию /(г, л) = г «'s'» в формулу (6.21), получим.

1 1.

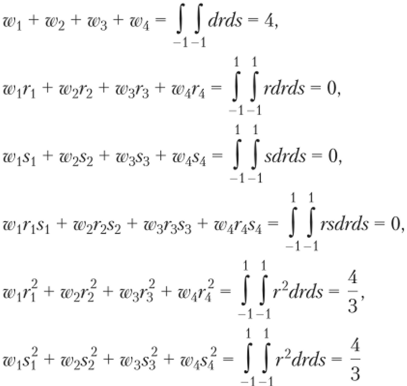
и т.д.

Если мы наложим некоторые условия на расположение узлов, то эти уравнения можно упростить. Предположим, ЧТО (Г], 5,) = (-р, у), (Г_Ъ s₂) = (Р, у), (г₃, 5₃) = (Р, -у) И (г₄, 5₄) = = (-р, -у), тогда система (6.22) принимает вид.

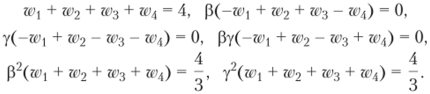
Теперь мы имеем шесть уравнений для шести неизвестных П1^½

и решение этой системы: р = у = - и т^⁼ 1, k = 1,4. Тогда кубатурная формула (6.21) приобретает вид.

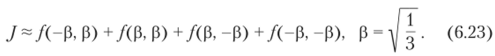
Это в точности дает двумерную формулу Гаусса, которая может быть также получена по правилу перемножения для М = 2. Мы можем расположить узлы и некоторым другим способом, например (г_ь Sj) = (-р, 0), (r₂, s₂) ⁼ (0, Р), (r₃, s₃) = = (Р, 0) и (/4, х₄) = (0, -р). Решая уравнения (6.22), мы полуf 21^½

чим р = - и Wh = 1, k = 1,…, 4, и теперь кубатурная формула (6.21) записывается в виде.

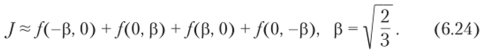
На основе полученных выше формул построим формулы интегрирования по произвольной прямоугольной области S = {а < х < Ь, с у < d}. Вначале разобьем область 5 на ячейки, вводя сетку с узлами (х_п, у_т), которая задается следующим образом:

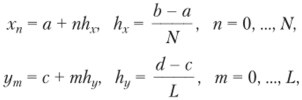
где h_x и hy определяют размер каждой ячейки.

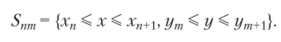
Используя формулы, полученные для интеграла (6.20) и сделав замену переменных х = 0.5(х" + х"₊₁) + 0, 5h_xr и у =.

= 0.5(у", + у_т+]) + 0.5hySy мы сначала вычислим интегралы по каждой ячейке S_nmt а затем просуммируем все полученные значения. В результате мы придем к следующим формулам:

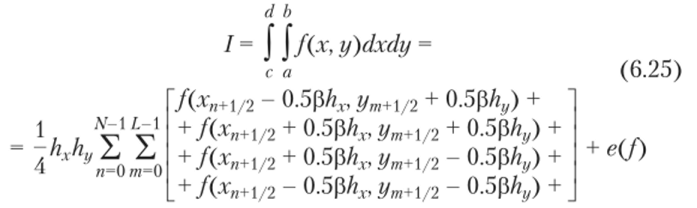
на основе кубатуры (6.23) и.

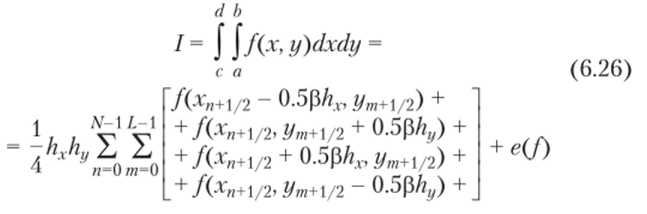
на основе кубатуры (6.24). Точка (*, 7+½, z/w+½) обозначает центр ячейки и имеет координаты х_п+{/₂ = х_п + 0.5h_x и у_П1+/₂ ⁼ = у_т + 0.5h_y. Формулы (6.23) и (6.24) точны для всех одночленов вида х^ту^т, п > 0, т > 0, п + т > 3. Тогда выражение для ошибки формул (6.25) и (6.26) можно записать в виде.

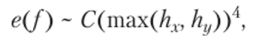
где константа С зависит от частных производных функции f (x, у) и мы предполагаем, что все эти производные непрерывны. Для того чтобы вычислить интеграл с заданной точностью, мы можем использовать метод, представленный в параграфе 6.2, только теперь 4 будет обозначать приближенное значение интеграла, вычисленное при делении области интегрирования на х L_k ячеек, где.

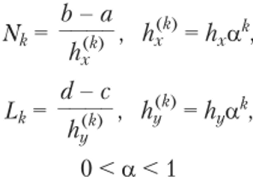
представляют сооой число подинтервалов в направлениях х и у соответственно.

Пример 6.6 (вычисление двумерного интеграла) Рассмотрим следующий интеграл.

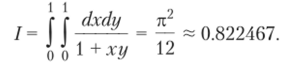
Для вычисления этого интеграла мы воспользуемся кубатурной формулой (6.25). Выберем начальный шаг h_x = h_y= h = 1 и будем последовательно уменьшать его в два раза (а = 0.5). Результаты вычислений представлены в табл. 6.3.

Таблица 63

Этот пример показывает, что приближенные значения интеграла, вычисленные по формуле (6.24), сходятся очень быстро к точному значению интеграла.

Используя рассмотренный выше подход, можно построить формулы интегрирования и для интегралов более высокой размерности. Например, рассмотрим трехмерный интеграл.

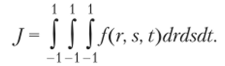
В этом случае трехмерный аналог кубатурной формулы (6.26) имеет вид.

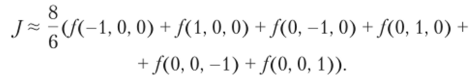
Тогда формула интегрирования по прямоугольному параллелепипеду записывается в следующем виде:

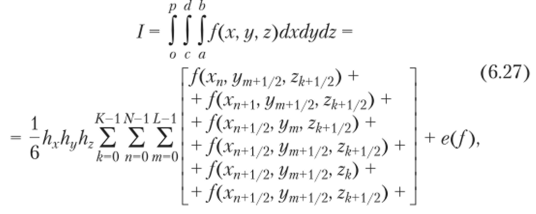
где.

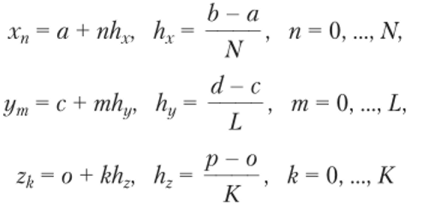
и.

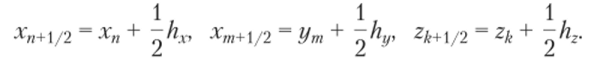
До сих нор мы обсуждали интегрирование, но прямоугольным областям, но рассмотренные выше методы имеют более широкую область применения. Дело в том, что при помощи подходящей замены переменных некоторые регулярные области могут быть преобразованы в прямоугольные области. В частности, это касается таких областей, как круг, сфера, эллипс, эллипсоид и цилиндр (более подробная информация представлена в Приложении Б). Например, чтобы вычислить интеграл по кругу, перейдем в полярные координаты и после преобразования получим.

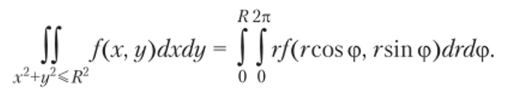
Таким образом, исходный интеграл превращается в интеграл по прямоугольнику 0 </*</?, О < (р < 2л.

Более серьезная проблема возникает, если нам нужно вычислить интеграл по некоторой нерегулярной области. Предположим, дана область S, показанная на рис. 6.6, и нам необходимо приближенно вычислить.

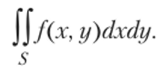
При этом появляется дополнительная задача: как представить область S? Наиболее простой способ — приблизить границу S ломаной линией, а затем представить область S как набор треугольников (рис. 6.6). Эта процедура называется триангуляцией. Теперь, для того чтобы получить значение интеграла по области S, мы должны вычислить объемы всех прямых треугольных призм, где высоты этих призм определяются функцией /(х, у).

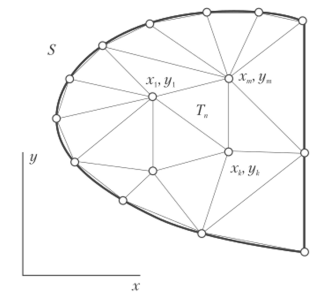
Рис. 6.6. Триангуляция нерегулярной области.

Прежде чем выводить формулу интегрирования по области 5, мы построим кубатурную формулу для стандартного треугольника Т с вершинами (0, 0), (0, 1) и (1, 0) (рис. 6.7).

Если применить рассмотренный выше подход (см. выражения (6.21) и (6.22)), то можно получить следующие формулы:

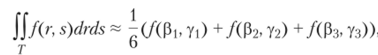
где.

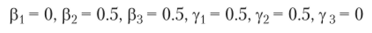
или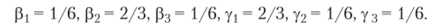

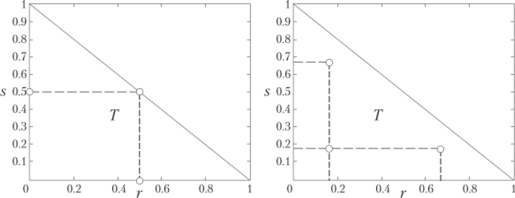
Рис. 6.7. Узлы интегрирования для стандартного треугольника.

Можно проверить, что приведенная выше формула точна для одночленов вида 1, х, у, х², ху, у². Трансформируя стандартный треугольник, можно получить формулу интегрирования по произвольному треугольнику Т_п с вершинами.

(х[^п yf), (х^п yjⁿ⁾), (х⁽_п'^г>, у^). Суммируя значения интегралов по всем таким треугольникам, мы придем к общей формуле интегрирования по произвольной области S:

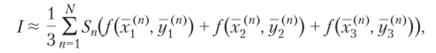
где.

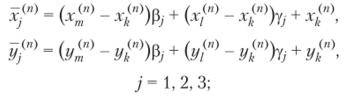
S" — площадь треугольника Т_п:

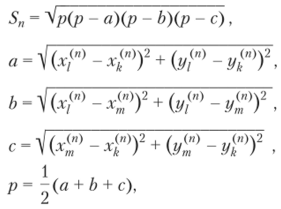
N — число треугольников, приближающих область S.

Аналогичный подход может быть применен для численного интегрирования по нерегулярной трехмерной области. В этом случае такая область представляется как набор тетраэдров.