Полное исследование уравнения парной линейной регрессии

Процесс полного исследования уравнения рассмотрим на следующем примере.

Пример 3.6.

По данным, приведенным в табл. 3.3, построим уравнение парной линейной регрессии и проведем его полное исследование. Примем доверительную вероятность у = 0,95 (проверка предпосылок 2 и 3 МИК (см. параграф 3.3) будет произведена далее в гл. 5 и 6). Результаты, полученные аналитически, сравним с результатами, полученными при работе с инструментом «Регрессия» Microsoft Excel.

Таблица 33

Исходные данные для примера 3.6.

Часть 1. Аналитическое решение задачи.

1. Построение уравнения регрессии.

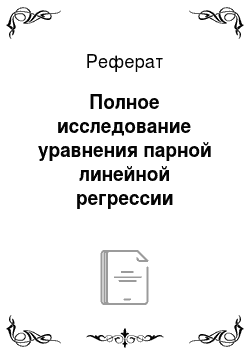
В результате расчетов (показаны в параграфе 3.2) получено: 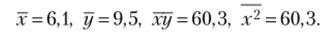По формулам (3.11) имеем.

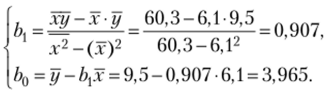
Получено уравнение линейной регрессии у_{ = 3,965 + 0,907.г*_;.

2. Проверка значимости полученного уравнения регрессии.

В результате расчетов (показано в параграфе 3.4) получено.

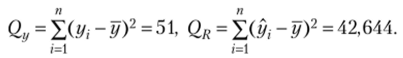
Коэффициент детерминации (3.19).

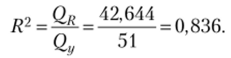
Получено высокое значение коэффициента детерминации, что говорит о хорошем качестве построенного уравнения регрессии.

Проверим статистическую значимость R² (формула (3.22)):

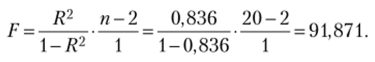
Критическое значение статистики Фишера для, а = 0,05 с Vj = 1, v₂ = 20 — 2 = 18 степенями свободы F_Kp = F (0,05; 1; 18) = 4,41.

Так как F> F_Kp, наше уравнение регрессии статистически значимо.

3. Проверка значимости коэффициентов регрессии /;₀ и by

В результате расчетов (см. параграф 3.5) получено.

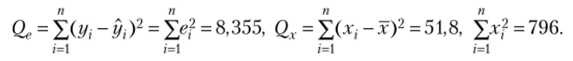
Стандартная ошибка (среднее квадратическое отклонение) коэффициента регрессии /;, (формула (3.26)):

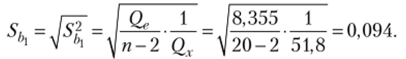
Статистическая значимость коэффициента Ь_{ (формула (3.24)):

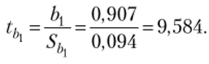
Стандартная ошибка (среднее квадратическое отклонение) коэффициента регрессии Ь₀ (3.28):

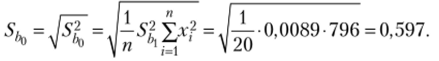
Статистическая значимость коэффициента Ь₀:

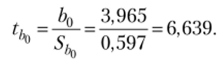
Критическое значение статистики Стыодента при уровне значимости, а = 0,05 и числе степеней свободы v = 20 — 2 = 18 ?_кр = /(0,05; 18) = 2,1.

Так как наблюдаемые значения статистики для коэффициентов Ь₀ и Ь больше критического значения, оба коэффициента регрессии статистически значимы.

4. Взаимосвязь критериев.

Найдем коэффициент корреляции (2.9):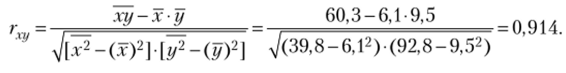

Статистика коэффициента корреляции.

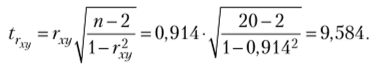
Ранее получено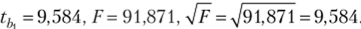

Связь между этими критериями (3.29) подтверждена: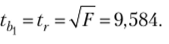

5. Нахождение доверительных интервалов для коэффициентов регрессии (см. параграф 3.6).

Имеем: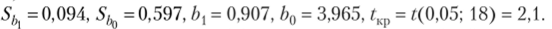

Доверительные интервалы для коэффициентов парной линейной регрессии (3.35):

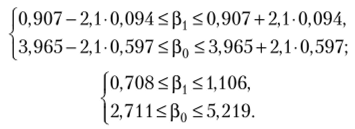
6. Точечный и интервальный прогнозы для модели парной регрессии (см. параграф 3.7).

Ранее получено:

выборочная дисперсия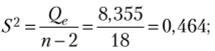

среднее значение объясняющей переменной х = 6,1; Q_x = 51,8.

Примем: доверительная вероятность у = 0,95.

Критическая точка /;_|ф = ?_{0 0Г); 18} = 2,1.

Прогнозы оценим для значений х₍₎ = х, х_п = х_тах = 9, х₀ = x_max = 3.

Рассчитаем прогнозное (точечное) значение зависимой переменной по уравнению регрессии: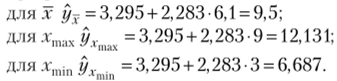

6.1. Доверительный интервал прогноза среднего значения зависимой переменной.

Дисперсия интервального прогноза среднего значения у (3.39) для всех трех значений объясняющей пепемениой: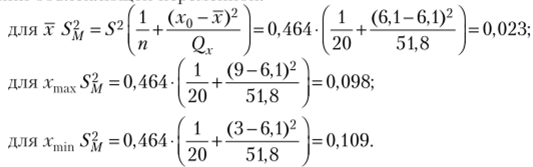

Ошибка прогноза среднего значения Д_м:

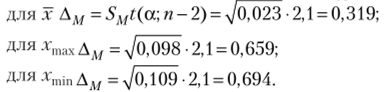
Доверительный интервал (3.38) для всех трех рассчитанных по уравнению значений объясняющей переменной:

для х 9,5−0,319 < М (у | .г = х) < 9,5 + 0,319,9,181 < М (у х = х) < 9,819;

для *_тах 12,131 — 0,659 < М (у | г = л'_тах) < 12,131 + 0,659, 11,472 < М (у х = х_тах) < < 12,790;

для x_min 6,687 — 0,694 < М (у х = лг_{т (п}) < 6,687 + 0,694, 5,993 < М (у х = x_min) < 7,381.

6.2. Доверительный интервал прогноза индивидуального значения зависимой переменной.

Дисперсия интервального прогноза индивидуального значения t/J (3.41) для всех трех значений объясняющей переменной:

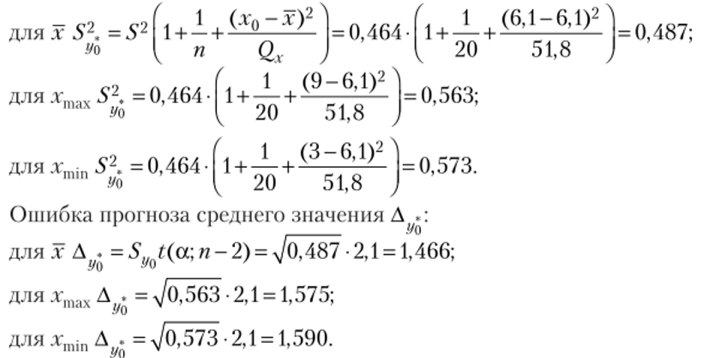
Доверительный интервал (3.40) для всех трех индивидуальных значений объясняющей переменной: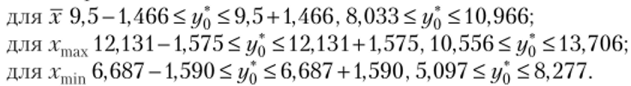

На рис. 3.4 схематически представлено поведение среднего и индивидуального значений зависимой переменной у как функция от объясняющей переменной х. Ясно, что доверительный интервал для индивидуальных значений объясняющей переменной шире, чем доверительный интервал для математического ожидания.

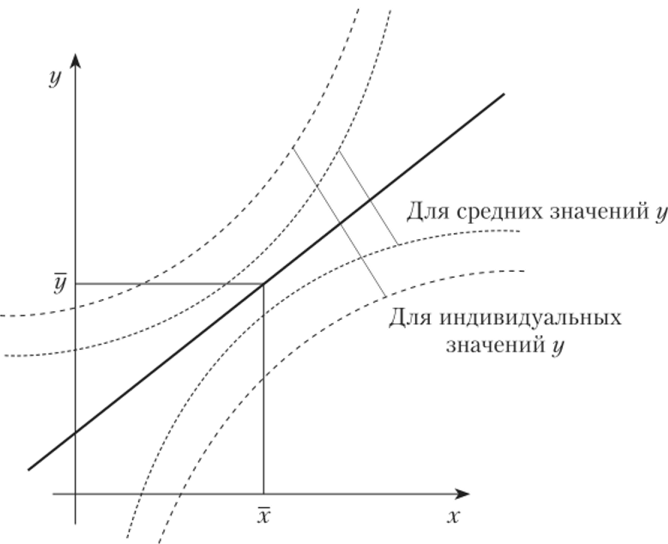
Рис. ЗА. Поведение среднего и индивидуального значений зависимой переменной.

7. Средняя ошибка аппроксимации ищется по формуле (3.42):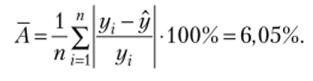

Часть 2. Решение задачи с использованием инструмента «Регрессия» Microsoft Excel.

Вводим исходные данные в лист таблицы Microsoft Excel и вызываем надстройку «Регрессия» пакета «Анализ данных». Вводим входные интервалы у и х, ставим галочку в графе «Метки», ставим галочку в графе «Уровень значимости» и в окошко вводим величину 99%, вводим ячейку выходного интервала и ставим галочку в графе «Остатки». Выполнив указанные действия, нажимаем ОК (рис. 3.5).

Результаты представлены на рис. 3.6.

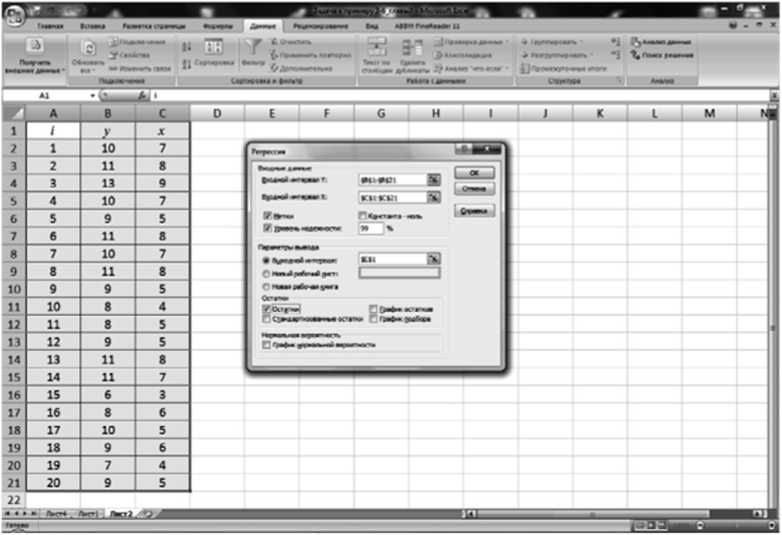
Рис. 35. Ввод исходных данных.

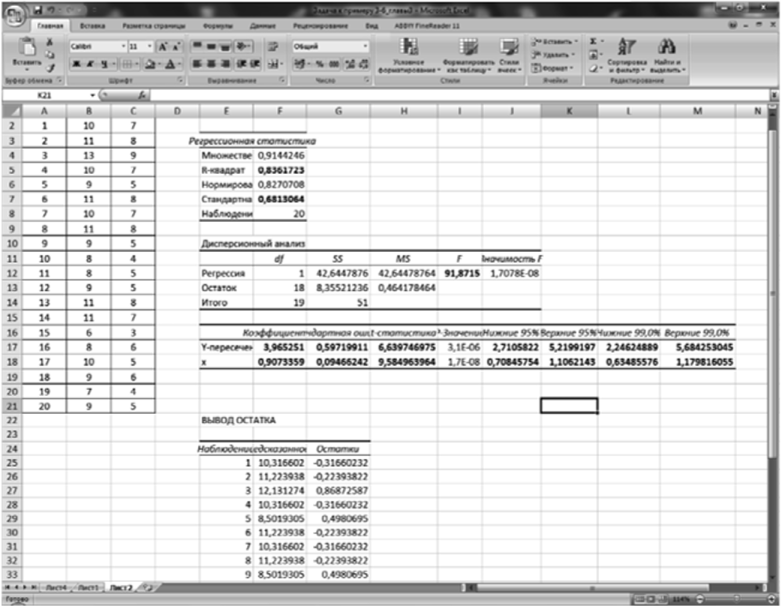
Рис. 3.6. Получение результатов решения.

Использовав инструмент «Регрессия», ответили на первые пять пунктов задачи. Все нужные числа на рис. 3.6 выделены.

• 1. Коэффициенты уравнения регрессии Ь₀ = 3,965, b_i = 0,907.
• 2. Коэффициент детерминации R² = 0,836.

Статистика Фишера F= 91,875. Критическое значение найдем, используя функцию РРАСПРОБР (всроятность; степени свободы₁; степени свободь^)^[1]:

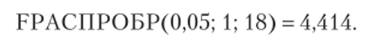
Так как наблюдаемое значение /‘'больше критического, то наше уравнение значимо.

3. Значимость коэффициентов:

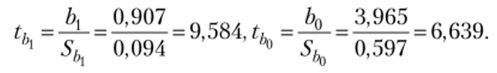
Критическое значение статистики Стьюдента при уровне значимости, а = 0,05 и числе степеней свободы v = 20 — 2 = 18 найдем с помощью функции СТЬЮДРЛСПОБР (вероятность; степейи_свободы):

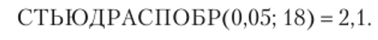
Так как наблюдаемые значения статистик больше критического, оба коэффициента уравнения регрессии значимы.

4. Для того чтобы проверить взаимосвязь критериев, необходимо найти коэффициент корреляции. Сделаем это на отдельном листе, используя функцию «Корреляция» в настройке «Анализ данных» (рис. 3.7).

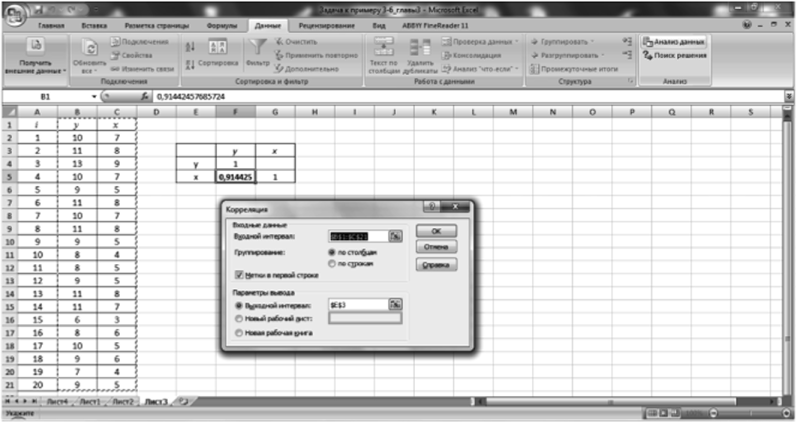
Рис. 3.7. Расчет корреляции.

Аналогично предыдущему вводим во «Входной интервал» оба столбца значений у и х_у данные расположены «но столбцам», ставим галочки «Метки в первой строке» и вводим в окошко «Выходной интервал». Нажимаем кнопку ОК. Результат представлен на этом же рисунке: коэффициент корреляции г_су = 0,914. Рассчитаем статистику коэффициента корреляции: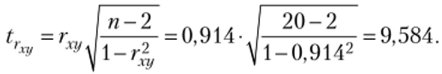

Теперь можем проверить взаимосвязь критериев:

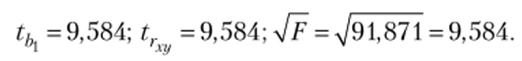
5. Доверительные интервалы для коэффициентов регрессии для двух значений доверительной вероятности возьмем из таблицы результата работы инструмента «Регрессия» (см. рис. 3.6):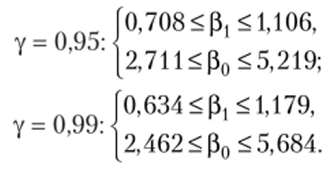

Чем больше доверительная вероятность, тем шире доверительный интервал.

6. Расчет доверительных интервалов зависимой переменной начинаем с нахождения требуемых по условию значений объясняющей переменной. Находить эти значения будем с помощью соответствующих функций программы Microsoft Excel:

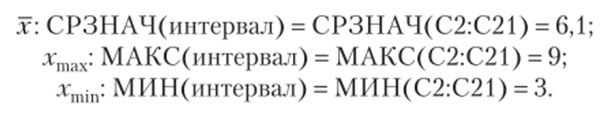
Дальнейшее решение по п. 6 части 1 — среднее квадратическое отклонение — возьмем из таблицы на рис. 3.6 «Стандартн.»: S = 0,681; ?_кр = 2,1.

7. Находим среднюю ошибку аппроксимации. Вновь вернемся к рис. 3.6. В его нижней части выведены расчетные значения зависимой переменной по уравнению регрессии и остатки. Остатки есть разности (отклонения) между наблюдаемым и рассчитанным значением зависимой переменной. Введем еще два столбца: ABS (c,) — абсолютная величина разности и ABS(е)/у_} — отношение разности к наблюдаемой зависимой величине. Результаты последнего столбца просуммируем и разделим на число наблюдений. Умножив на 100%, получим среднюю ошибку аппроксимации (рис. 3.8).

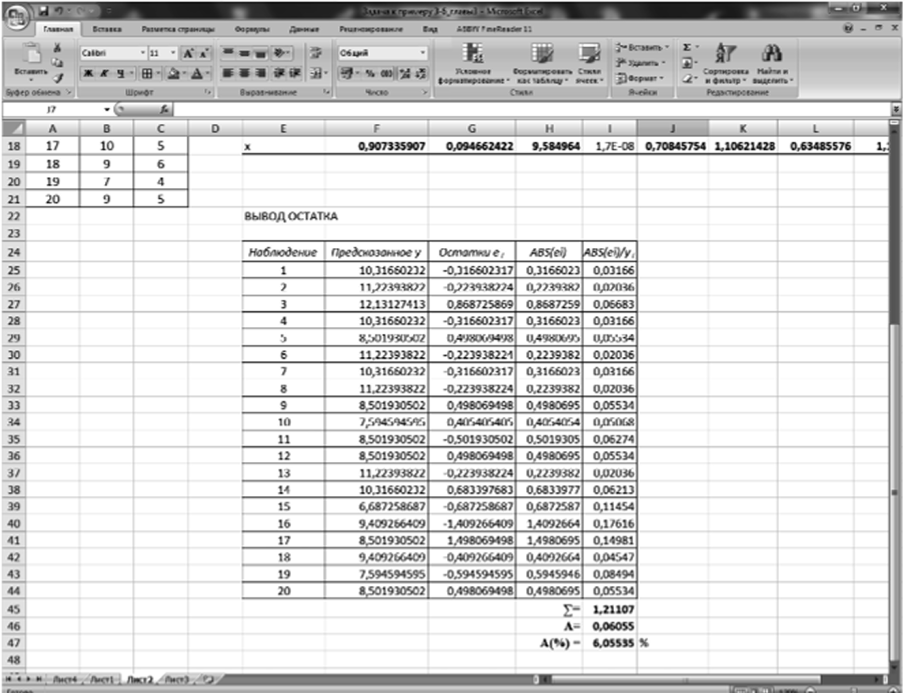
Рис. 3.8. Получение средней ошибки аппроксимации.

Средняя ошибка аппроксимации (формула (3.42)) А = 6,05%, что говорит о хорошем качестве модели регрессии.

Вывод. Результаты аналитического решения примера полностью совпадают с результатами, полученными с использованием инструмента «Регрессия» Microsoft Excel.

* * *.

Ограниченность парной линейной регрессии заключается в следующем.

• 1. В реальном экономическом процессе никакая единственная переменная, за редкими исключениями, не в состоянии хорошо объяснить изменения зависимой переменной.
• 2. Могут существовать несколько одинаково хороших и взаимно противоречивых парных регрессий: линейная или нелинейная.
• 3. Линейная форма — самая простая.

Однако нет ничего лучше по простоте и ясности объяснения парной линейной связи. При равной объясняющей способности из двух моделей всегда выбираем более простую.

Завершая гл. 3, необходимо отметить следующее: базовые принципы эконометрического анализа опираются на знание парного линейного регрессионного анализа. Только глубоко изучив и поняв его, можно понимать и все остальное в эконометрике.

Замечание 3.6. В этой главе рассмотрен только один метод определения коэффициентов регрессии — метод наименьших квадратов. Существуют и другие методы определения коэффициентов регрессии:

• • метод наименьших модулей (МНМ);
• • метод моментов (ММ);
• • метод максимального правдоподобия (ММП).

Рассмотрение и изучение этих методов выходит за рамки данной книги.

• [1] Все расчеты в книге выполнены в MS Excel 2007. В приложении приведено названиеэтих же функций в MS Excel 2013.