Средние обобщающие величины

В качестве структурных средних чаще всего используют показатели моды (Мо) — наиболее часто повторяющегося значения признака, к медианы (Me) — величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой — не меньше его. В табл. 12.7… Читать ещё >
Средние обобщающие величины (реферат, курсовая, диплом, контрольная)
Они играют исключительно важную роль в статистических исследованиях социальных процессов и явлений. Только с помощью средних можно охарактеризовать совокупности по количественному варьирующему признаку, но которому можно их сравнивать.
Рассмотрим основные виды средних величии.
Средняя арифметическая — самый распространенный вид средних величин. Вычисляется как отношение суммы всех вариантов (значений) признака к количеству вариантов. Например, у пяти судей в производстве находится 17, 20, 45, 37, 21 дел соответственно. Тогда средняя нагрузка судьи (х) вычисляется следующим образом:
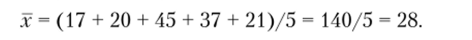
Это простая средняя арифметическая.
Рассмотрим другой пример (табл. 12.6).
Таблица 12.6
Сведения о делах, находящихся в производстве.
Число дел (варианта х) | Число судей (частота/). | Произведение вариант и частот {xf) |
I.V = 94. | и- 15. | I xf = 360. |
В этом примере приведены данные о количестве дел, находящихся в производстве, для 15 судей. Причем некоторые данные совпадают. Так, у трех судей на рассмотрении находится по 15 дел, у девяти — по 27, у двух — по 20. В этом случае для вычисления среднего показателя нагрузки судьи используется взвешенная средняя арифметическая (х), которая представляет собой отношение суммы произведений всех значений изучаемого признака (варианты) на частоту его встречаемости (xf) к общему числу вариант (/).
Таким образом, средний показатель нагрузки судьи (х) равен.
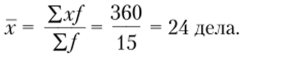
Некоторые особенности есть при расчете гак называемого интервального ряда, когда изучаемый признак принимает значение из некоторого интервала.
Например, рассмотрим задачу определения среднего возраста осужденных для статистических данных, приведенных в табл. 12.7.
Таблица 12.7
Вычисление среднего возраста осужденных
Возраст осужденных (варианта .г). | Число осужденных (частота /) | Середина интервалов. (0. | Произведение середины интервалов и частоты. Of) |
От 16 до 18. | 17,0. | 34,0. | |
От 18 до 25. | 21,5. | 322,5. | |
От 25 до 29. | 27,0. | 594,0. | |
От 29 до 35. | 32,0. | 608,0. | |
От 35 до 45. | 40,0. | 1360,0. | |
?/=92. | ?;/= 2918,5. |
В табл. 12.7 приведены данные о количестве осужденных для различных возрастных групп. Для вычисления среднего возраста осужденных сначала определяют середину интервала для каждой возрастной группы (/) как простую среднюю арифметическую границ возрастного интервала. Например, для возрастной группы от 16 до 18 лег середина интервала определяется как / = (16+ 18)/2 = 17 лег.
Дальше вычисление среднего возраста осужденных (х) проводят, но формуле вычисления средней взвешенной:
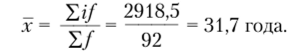
Рассмотрим другой средний показатель — среднюю геометрическую. Данная величина в юридической практике используется для вычисления средних темпов роста и прироста (снижения) наблюдаемых явлений. Изучение этих параметров в динамике преступности, судимости и других юридических процессов имеет важное значение.
Познакомимся со средней геометрической на примере динамики взяточничества в России (табл. 12.8).
Таблица 12.8
Динамика взяточничества в России (2009—2013 гг.)
Показатели. | |||||
Абсолютный показатель учтенных деяний. | |||||
Абсолютный годовой прирост. | — 32. | ||||
Темпы роста к предыдущему году, %. | 99,3. | 111,5. | 102,8. | 103,5. | |
Годовые темпы прироста, %. | — 0,7. | 11,5. | 2,8. | 3,5. |
Для того чтобы вычислить среднегодовые темпы роста взяточничества, нельзя брать среднюю арифметическую годовых темпов роста, так как она завысит реальный среднегодовой прирост. В статистике для характеристики динамических процессов используют средний геометрический показатель.
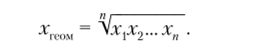
Следовательно, среднегодовой темн роста взяточничества будет равен.
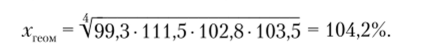
Средняя арифметическая, средняя геометрическая и другие средние — это своеобразная статистическая абстракция, поскольку они, отвлекаясь от истинных величин, отражают то общее, что присуще всей совокупности изучаемых единиц в совокупности. Величины средних часто выражаются дробными числами (102,5 исков, 25,9 правонарушений, 17,8 человек личного состава и т. д.), которых в жизни не бывает. Наряду с абстрактными средними в статистике используют конкретные средние, величины которых присутствуют в ряду статистических данных.
Этот особый вид средних величин — структурные средние — применяется для изучения внутреннего строения рядов распределения значений признака, а также для определения средней величины, если, но имеющимся статистическим данным ее расчет не может быть выполнен (например, отсутствует часть необходимых данных).
В качестве структурных средних чаще всего используют показатели моды (Мо) — наиболее часто повторяющегося значения признака, к медианы (Me) — величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой — не меньше его.
Обратимся к условному примеру вариационного ряда распределения осужденных по возрасту, приведенного в табл. 12.9.
Таблица 12.9
Распределение осужденных, но возрасту.
Возраст, лет. | |||||||||||||
Число осужденных. |
Медианой в этом ряду будет значение «20 лет» с частотой 150 осужденных. По обе стороны от нее находится равное число единиц совокупности. Модой в этом ряду является варианта «22 года» с наибольшей частотой — 175 осужденных.
В практике мода и медиана иногда используются вместо средней арифметической или вместе с ней. При использовании вместе они дополняют друг друга, особенно когда в совокупности небольшое число единиц с очень большим или очень малым значениями исследуемого признака.