Формальная логика А. де Моргана

Август (Огест) де Моргай (1806— 1871) родился в Индии, в семье полковника английских войск, получил высшее образование в Кембриджском университете. В 1828—1831 и 1836— 1866 гг. он состоял профессором математики Лондонского университетского колледжа; среди его учеников были И. Тодгентер и Дж. Сильвестр. В 1865 г. он, как первый президент Лондонского математического общества, открыл своей вступительной речью его заседания. Де Морган сделал ряд открытий в алгебре и анализе, о которых будет сказано далее. В одной статье 1838 г. он ввел термин «математическая индукция», который затем получил широкое распространение благодаря учебнику алгебры Тодгентера. В математике, как и в ее преподавании, де Моргана интересовали более всего основные принципы и их строгое логическое развитие. Математику и логику он называл очами точного знания и выражал сожаление, что математики не более заботятся о логике, чем логики о математике. Сам он стремился сблизить обе науки, и его главной заслугой явилось построение логики по подобию математических наук.

В своей «Формальной логике, или исчислении необходимых и вероятных заключений»^[1] де Морган исходил из принципа, что логика должна служить точным выражением мыслей и устранять присущие обыденному языку неясности и двусмысленности.

В каждом языке существуют так называемые положительные и отрицательные термины. Но это подразделение в значительной мере случайно — в одном языке может существовать отрицательный парный термин для данного термина, в другом языке он необязательно имеется. Да и в каждом языке не все термины снабжены соответствующими отрицательными терминами. Тем не менее каждый термин разделяет «совокупность сущностей» на две группы: обладающие и не обладающие отмеченными данным термином признаками. Каждое имя, таким образом, имеет свое отрицание, например «совершенный» и «не-совершенный», «человек» и «не-человек». Логика не только должна учитывать этот факт, но и выражать его. Однако с отрицанием в логике всегда существовали трудности. Выражаясь словами В. Минто, в логике отрицать какое-нибудь качество — значит просто утверждать, что оно принадлежит данному предмету, отрицание только уничтожает, устраняет, но не позволяет ничего подразумевать: «„Не-/;“ есть нечто совершенно неопределенное: оно может заключать в себе все, что угодно, кроме Ь» ^[2]. Для устранения такой неопределенности отрицания де Морган вводит в рассмотрение понятие «целого», или «универсума», выбираемого в зависимости от предмета исследования. Так, если X означает некоторый класс предметов (правда, де Морган чаще говорит об именах, обозначающих предметы), то все то в «целом» («универсуме»), что не есть X, следует считать за не-Х. Если для не-Х ввести обозначение х, то в результате станет очевидным отсутствие принципиальной разницы между отрицательными и утвердительными предложениями: «никакое X не У» означает, то же самое, что «все X суть не-У», т. е. «все X суть у».

Установив, что с указанной точки зрения X и х равноправны, де Морган вместо пары терминов предложений традиционной силлогистики X и У рассматривает четыре пары X, У; х, у X, у х, У, дающие 16 логически возможных комбинаций, из которых различны восемь. Для них де Морган использует двоякие обозначения: буквы A_v Е_{, /_1? 0_{, А', Е, /', О', указывающие на связь с обозначениями элементарных предложений традиционной силлогистики, и знаки Х) У^ Х. У; Х: У; ХУ; х)у и т. д.:

А{. «каждый X есть У» — Х) У; А': «каждый х есть у» — х) у

Е{. «ни один X не есть У» — Х. У; Е: «ни один х не есть у» — х. у;

• 1_{: «некоторые X суть У» — ХУ; Г: «некоторые х суть у» — ху;
• 0{. «некоторые X не суть У» — Х: У; О': «некоторые х не суть у» — ху.

Для этих предложений, называемых им простыми (simple), де Морган устанавливает следующие равносильности:

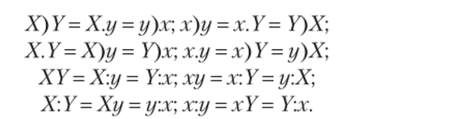
Здесь знак «=» используется де Морганом в смысле равносильности В другом смысле он использует этот знак в выражении Х) У + Y)Z = X) Z, где «=» означает «следовательно».

Используя знак «+» для конъюнктивной связи простых предложений, де Морган строит составные (complex) предложения или отношения:

В обычной для нас символике D есть «X = У», D, есть «X с У», D' есть «X D У», С есть «X = у», С_{ есть «X с у», С есть «X з у», Р означает, что ни один из классов Хп У, X п у, х п У, хпу не пуст.

Введенные таким образом отношения являются исходными для построения теории силлогизмов де Моргана. Силлогизмы, посылками которых служат составные предложения, он называет составными {complex syllogism) и отмечает, что, с его точки зрения, и составные предложения, и составные силлогизмы проще традиционных простых. Не вдаваясь подробнее в теории силлогизмов де Моргана, отметим следующее обстоятельство. В качестве силлогистических терминов де Морган использует сначала так называемые простые имена (простые термины) X, У, Z и т. д. Затем он вводит^[3]

в рассмотрение составные имена (составные термины): Р^есть имя того, что «есть сразу Ри Q» (т.е. Рп Q в символике теории классов), Р * Q^[4] есть имя того, что «есть Р или Q, или Р и Q сразу» (т.е. Р u Q). U — имя универсума, и — имя отрицания универсума (т.е. пустого множества). Введя то, что мы бы теперь назвали операциями пересечения и объединения, де Морган устанавливает такие свойства, как XU = Х Xu = X * U = U, X * и = = X, формулирует законы ^{[5], называемые теперь «законами де Моргана»: P+Q = P*Q; Р*(2 = P + Q, устанавливает дистрибутивность (Р* Q)(R * 5) = = PR * PS * QR * Q5, а затем строит теорию силлогизмов, используя составные имена в качестве субъектов и предикатов посылок.}

Таким образом, в своей теории силлогизмов де Морган использовал систему, названную позже алгеброй Буля. Эта система впервые отчетливо появилась у С. Джевонса. Позже де Морган ввел общее понятие отношения и операции над отношениями. Этим он фактически заложил фундамент современной теории отношений, развитой в дальнейшем в различных направлениях и с разных точек зрения Ч. Пирсом, Э. Шредером, Дж. Пеано, Г. Кантором, Г. Фреге, Б. Расселом. Де Моргану часто делали замечание о том, что его остроумные и оригинальные идеи в его изложении терялись из-за перегрузки этого изложения деталями, а также многочисленными и новыми обозначениями. Подчеркивание разнообразных оттенков смысла значения терминов также затрудняло восприятие его идей, разбивало впечатление, не оставляло представления о системе в целом. Несмотря на это, глубина и точность наблюдений, новизна и многообразие идей в его произведениях позволяют думать, что наследие де Моргана ценно, да и изучено оно далеко не полностью.

Алгебра логики Дж. Буля. Почти в одно время с де Морганом выступил с логико-математическими работами Дж. Буль (1815—1864), сын сапожного мастера, увлекавшегося математикой и изготовлением оптических приборов. Деловые качества Буля-отца были весьма посредственными, и он не смог дать сыну высшее образование. Булю удалось окончить только начальную школу, дальнейшие знания он приобретал самостоятельно. Так, он изучил многие языки. Рано приняв решение отдаться всецело математике, он без посторонней помощи проштудировал «Математические начала» И. Ньютона, «Аналитическую механику» Ж. Л. Лагранжа и другие научные труды. На жизнь он зарабатывал, работая учителем.

Буль начал свои математические исследования с разработки операторных методов анализа и теории дифференциальных уравнений. А потом, как и де Морган, с которым он подружился, Буль занялся математической логикой. Младшая дочь Буля Этель-Лилиан, в замужестве Войнич, прославилась как автор ряда романов, самым известным из которых является «Овод» о борьбе карбонариев за независимость Италии, а главное — о ценностях долга и идеи, которые могут быть выше ценности самой жизни. Два основных труда Буля носят весьма характерные названия — «Математический анализ логики, являющийся опытом исчисления дедуктивного рассуждения»¹ и «Исследование законов мышления, на которых основаны математические теории логики и вероятности»^[6][7]. Именно в них были заложены основы современной математической логики.

Буль отчетливо осуществил так называемое количественное истолкование объектов логики и последовательно применял новый подход к решению проблем и задач логики. Этот новый подход с неизбежностью позволял не только изменить и расширить области традиционной логики, но также изменить и расширить символический язык алгебры: осуществлять выбор подходящей символики, операций и законов, определяющих эти операции и отражающих специфику объектов исследования, т. е., но существу, создать новое исчисление. Буль подчеркивал, что сущность этого исчисления заключается в особенностях операций и законов, которым подчинены эти операции: «Те, кто знаком с настоящим состоянием символической алгебры, отдают себе отчет в том, что обоснованность процессов анализа зависит не от интерпретации используемых символов, а только от законов их комбинирования. Каждая интерпретация, сохраняющая предложенные отношения, равно допустима, и подобный процесс анализа может, таким образом, при одной интерпретации представлять решение вопроса, связанного со свойствами чисел, при другой — решение геометрической задачи и при третьей — решение проблемы динамики или оптики. Необходимо подчеркнуть фундаментальность этого принципа…»^[8].

Стремясь перевести логику Аристотеля на алгебраический язык, Буль обратил внимание и на вероятностную логику. В один год со своим основным математико-логическим сочинением «Исследование законов мышления…» Буль опубликовал статью «Об условиях, которые ограничивают решение вопросов в теории вероятностей»^[9], в которой предвосхитил необходимость аксиоматического обоснования теории вероятностей. Вот что писал Буль в этой статье: «Претензии (теории вероятностей) принадлежать к чистой науке должны основываться на той степени, в которой она удовлетворяет следующим условиям…», и далее сформулировал три условия. Второе и третье из этих условий носят общенаучный характер: необходимость опытной проверки результатов и запрет ограничений на развитие науки. Первое же условие таково: «Принципы, на которых основаны ее (теории вероятностей) методы, должны быть аксиоматическими (о/ ап axiomatic nature)». Буль опередил свое время и в формулировке целей теории вероятностей, фактически повторив в одной из своих статей 1851 г. формулировку, данную в 1846 г. русским математиком II. Л. Чебышевым^[10]. Именно в этом состоит то принципиально новое, что внес Буль в представления об исчислении¹, в ясном осознании абстрактности исчисления, в том, что исчисление определяется теми законами, которым мы подчиним операции. В качестве исходных символов Буль принимает:

• 1) х, y, z — символы классов,
• 2) +, -, х — символы операций, вместо знака х он часто использует точку • или просто опускает знак операции,
• 3) = — знак тождества.

Выражение х • у употребляется Булем для обозначения класса всех тех и только тех элементов, которые являются элементами как класса х, так и класса у.

Если классы х и у не имеют общих элементов, то через х + у обозначается класс, состоящий из элементов класса х и элементов класса у. Если всякий элемент класса у является элементом класса х, то через х — у обозначается класс, состоящий из всех тех и только тех элементов х, которые не являются элементами у. Итак, на множестве классов Буль вводит три операции: •, +, при этом две последние определены не на любых парах классов, дополнительное определение их на любые пары до общепринятых теперь теоретико-множественных операций в силу специфики определения Буля возможно двумя путями:

• а) либо под х + у надо понимать объединение классов хи у независимо от того, пересекаются они или нет;
• б) либо иод х + у следует понимать симметрическую разность классов х и у у тогда х — у также должно означать симметрическую разность, ибо последняя обратна самой себе. Учитывая наличие универсума 1 в системе, первый путь ведет, по существу, к построению булевой алгебры, а второй — к построению булева кольца. Представление в форме булева кольца дано И. И. Жегалкиным^[11][12]. Отметим, что хотя операции, введенные Булем, определены не всюду, они представляют так называемую полную систему связок, т. е. все теоретико-множественные операции в них выразимы. Именно, пересечение х и у выражается через х • г/, дополнение х • у — через 1-х, объединение хи у — через ху + х (1 — г/) + г/(1 — х). Буль дает это выражение объединения классов через введенное им сложение^[13].

Термины «логическое уравнение», «логическая функция» Буль употребляет для обозначения какого-либо уравнения или функции, которые содержат символы классов х, у_}…

Примеры функций: /(х) = х, /(х) = (1 + х)/(1 — х), /(х, у) = (х — у)/(х — -2*/).

Если равенство х (1 -х) = 0 рассматривать как алгебраическое уравнение, т. е. считать х принимающим числовые значения, то это уравнение имеет корни 0 и 1. «Это наводит на мысль, — пишет Буль, — вместо определения меры согласованности символов логики с числовыми символами непосредственно сопоставлять логическим символам количественные символы, принимающие лишь значения 0 и I»¹. Исходя из этого замечания Буль принимает следующий общий способ обращения с логическими функциями и логическими уравнениями: «Поскольку процессы формального рассуждения зависят от законов, которым подчинены символы, а не от природы их интерпретации, мы позволим себе трактовать символы х, у, … так, как если бы они были количественными символами вышеописанного рода. Мы можем в действительности пренебречь логической интерпретацией символов данного уравнения, считать их количественными символами, принимающими лишь значения 0 и 1, выполнить над ними как таковыми все обычные приемы решения, а в конце возвратить им их логическую интерпретацию»^[13][15].

В соответствии с этим соглашением вместо символов х, г/, z, … в логические функции можно представить значения 0 и 1: если f (x) = {а + х):: (я — 2х), то/(0) = a/a, f ( 1) = (а + 1 )/(а — 2). При этом Буль многократно подчеркивает, что промежуточные результаты вовсе не обязательно будут иметь логическую интерпретацию.

Всякую функцию f (x) можно представить в виде f (x) = ах + /;(1 -х).

Действительно, полагая в этом равенстве х = 1, мы получим f (t) = а, при х = 0 будем иметь /(0) = /;, т. е.

Аналогично.

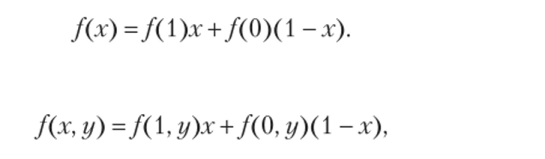
но так как.

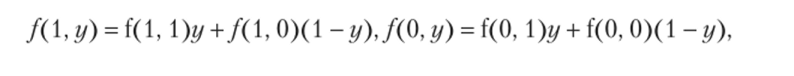
то.

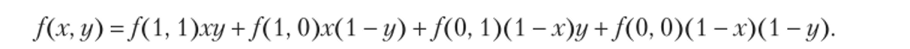
Множители 1и (1−1)в разложении функции f (x) и множители ху, х (1 — г/), (1 — х)у, (1 -х)(1 — у) в разложении/(х, у) Буль называет конституентами и формулирует общее правило разложения функций по конституентам:

• 1) составить полный набор конституент искомого разложения;
• 2) найти коэффициенты разложения;
• 3) умножить каждую коституенту на соответствующий коэффициент и результаты сложить.

Символическая логика Дж. Венна. Джон Венн (1834—1923), сын священника, окончил в 1858 г. один из колледжей Кембриджского университета. В соответствии с семейными традициями он какое-то время служил священником, но вернулся в Кембридж, где стал преподавать логику и мораль. Важнейшей из работ Венна, посвященных обоснованию и развитию новых методов логики, является «Символическая логика»¹.

Первой задачей символической логики Венн, подробно Булю и Джевонсу, считал создание специфического языка, который должен содействовать «расширению возможностей применения наших логических процессов при помощи символов»^[16][17]. В качестве символов классов Венн употребляет буквы латинского алфавита. Как и все логики того времени, пустой и универсальный классы он обозначает символами 0 и 1. Дополнение к классу х он обозначает через х. Кроме операций * и + (он понимает х + у как объединение классов), Венн вводит вычитание и деление.

Под х — у понимается исключение класса у из класса х при условии, что у есть часть х. Эту операцию он рассматривает как обратную к операции объединения классов, показывает, что она может быть исключена, поскольку в силу определения.

Операция деления рассматривается им как обратная к операции пересечения классов. Она истолковывается Венном следующим образом: запись х/у служит обозначением класса 2, такого, что х = yz в качестве 2 можно взять произвольный класс вида х + v-y^[18].

Очевидно, что деление в действительности сводится к сложению и умножению и может быть исключено. Однако Венн, чтобы подчеркнуть аналогию с арифметикой, сохраняет в своей системе операции вычитания и деления. Выражение х > 0 означает, но Венну, что класс х не пуст; оно рассматривается как отрицание к х = 0. Равенство х — у Венн понимает как «не существует предметов, принадлежащих х и не принадлежащих у, и предметов, принадлежащих у и не принадлежащих х», и записывает его в «нулевой форме»: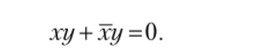

Венн формулирует некоторые свойства операций, например

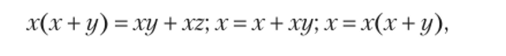
при этом он ограничивается иллюстрацией их на различных примерах, не пытаясь отделить постулируемые от доказываемых.

Как и другие представители алгебры логики конца XVIII — начала XIX вв., Венн считал важнейшими задачами символической логики решение уравнений и исключение неизвестных. Фактически он решал эти задачи так же, как и другие логики, и мы не будем подробно останавливаться на его методах решения равенств. В отличие от Буля и Джевонса, Венн решал не только уравнения, но и логические неравенства.

Пример 1.1.

Пусть дано неравенство.

Требуется найти необходимое и достаточное условие существования такого класса х, чтобы класс ах + Ьх + с был не пуст.

Решение. Необходимым и достаточным условием существования указан, но го класса является

Действительно, изд + 6 + с = 0 следует: а = О, b = 0, с = 0, т. е. ах + Ьх + с = О для любого х.

Пусть а + b + с > 0, это значит, что по крайней мере один из классов а, Ь, с не пуст. Если а > 0, положим х = а, тогда будем иметь.

аа + Ьа + с> 0.

При b > 0 возьмем х = b, получим.

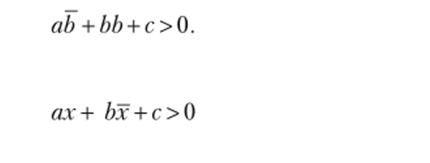
Если же с > 0, то для любого х.

Условие (1.3) Бонн называет результатом исключения х из (1.2).

Вени рассматривает и случаи, когда среди посылок имеются уравнения и неравенства, например

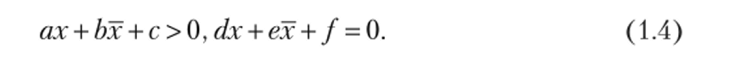
Пример 1.2.

Покажем, что необходимыми и достаточными условиями существования такого класса х, что класс ax + bx + с не пуст, а класс dx + ex + / пуст, являются.

Решение. Действительно, из равенства dx + ex + f = 0 следует dx = 0, ex = 0, f = 0,.

dex = 0, dex = 0, de (x + x) = 0, de = 0. Если dx = 0, ex = 0, to x откуда ax c ad, bx c be.

Если ax + bx+c> 0, то и подавно ad + be + c > 0.

Таким образом, из формул (1.4) следуют условия (1.5).

Пусть выполнены условия (1.5). Тогда de = 0,/= 0 и хотя бы один из классов ad, be, с не пуст. При ad >0 возьмем x = d, получим.

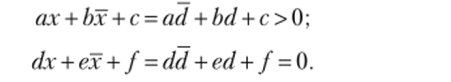
Если Ьё> 0, положим х-е, тогда.

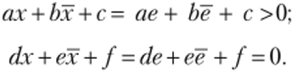
В случае с > 0 класс ах + Ьх не пуст для любого х, если взять х = е, то.

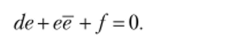
Следовательно, условия (1.5) достаточны для существования класса х, удовлетворяющего соотношениям (1.4).

При решении логических задач Вени использовал не только алгебраические методы, но и диаграммы, называемые теперь диаграммами Венна.

Построение диаграмм Венн начинает с разбиения плоскости на 2п областей посредством п замкнутых контуров, где п — число классов, заданных в условии задачи. В решаемых им задачах встречаются только случаи п < 5. С ростом числа переменных наглядность картинок резко уменьшается, поэтому для представления задач с большим числом классов Венн использовал таблицы, состоящие из 2п клеток, — таблицы Венна. Между таблицами и картинками имеется взаимно однозначное соответствие: по каждой таблице строится картинка, и наоборот, по каждой картинке пишется таблица. На рис. 1.6 построены диаграммы и таблицы для разных значений п.

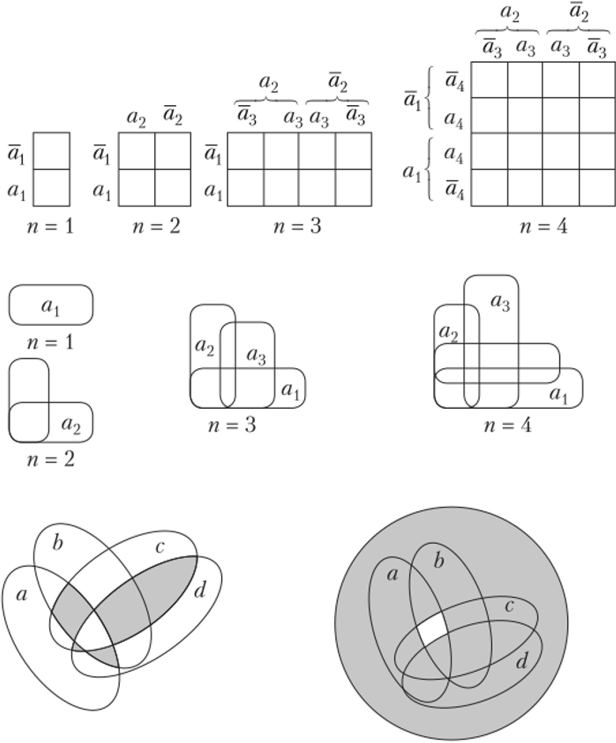
Рис. 1.6. Графическое представление связи логических переменных:

от 2 до 5.

Метод построения картинок и таблиц Вени демонстрирует на многочисленных примерах, однако не дает общего определения понятия диаграммы.

На основании анализа примеров диаграмм Венна для п переменных можно составить картинку или таблицу для п переменных, одни из ячеек которой могут быть заштрихованы, другие могут быть пустыми, а третьи — содержать звездочки. Заштрихованные ячейки соответствуют классам, противоречащим условиям задачи, т. е. подлежащим удалению по методу В. С. Джевонса. Уильям Стенли Джевонс (W. Stanly Jevons, 1835—1882) — английский логик, экономист, один из основателей неоклассического направления в экономической теории. В 1863—1876 гг. Джевонс преподавал в Манчестере (профессор логики, философии и политической экономии), а в 1876—1880 гг. — в Лондонском университетском колледже (та же должность). В вышедшей в 1874 г. книге «Основы науки — трактат о логике и научном методе» Джевонс сформулировал свой знаменитый тезис о том, что «наша наука должна быть математической хотя бы потому, что имеет дело с количествами». Эта книга представляет собой его главный труд по вопросам логики и методологии науки, в котором им фактически были заложены основы современной логики.

Внизу на рис. 1.6 показаны заштрихованные ячейки. Незаштрихованные ячейки составляют логические единицы высказываний. Звездочки позволяют выражать некоторые частные суждения. Надо заметить, что у Венна звездочка встречается только в одном примере. На диаграмме Всн_на для четырех переменных на рис. 1.6 заштрихованы ячейки abed, abed, abed, abed, abed. Диаграмма выражает предложение.

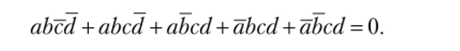
Иногда метод диаграмм Венна ведет к цели быстрее, чем аналитическое решение. Э. Шредер в «Лекциях по алгебре логики (точная логика)»^[19] проводит следующую задачу Джевонса.

Пример 1.3.

Требуется упростить посылки

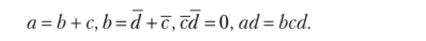
Решение. Заштриховав все области, пустые в силу условия задачи, из рис. 1.6 тотчас же получаем, что а = b = с = 1, d = 0. Этот же результат можно получить и аналитически.

Часто считают, что Венн воспринял идею кругов Эйлера и внес в метод Эйлера лишь некоторые улучшения. С этим мнением, однако, нельзя согласиться. Общим в методах Эйлера и Венна является лишь то, что оба они связаны с представлением объемов понятий на плоскости. В основе метода диаграмм Венна лежит отсутствовавшая у Эйлера идея разложения на конституенты — одна из центральных в алгебре логики. Диаграммы, построенные с учетом разложения на конституенты, не только более наглядны, но и позволяют извлекать большую информацию из условий задачи. К тому же — и в этом состоит еще одно важное отличие диаграмм Венна — они строились не только с целью иллюстрировать уже имеющееся решение, но и как аппарат для решения логических задач.

Алгебра логики Э. Шредера и П. С. Порецкого. Одновременно с работами Венна публиковались работы Э. Шредера и П. С. Порецкого.

Эрнест Шредер (1841 — 1902) — немецкий алгебраист и логик, с 1874 г. — профессор политехникума в Дармштадте, с 1976 г. — высшей технической школы в Карлсруэ. В работах Шредера получила дальнейшее развитие алгебра логики, называемая им логическим исчислением (Logikkalkul). Ему принадлежит и термин «исчисление высказываний» (Aussagenkalkul). Шредер, как и Джевонс, считал излишним в логике операции вычитания и деления. Он строил систему с операциями •, +, -i, тождеством = и константами 0 и 1. В отличие от Буля, Джевонса и Венна, Шредер явно указывал, какие из свойств операции он принимает в качестве аксиом, а какие получает как теоремы. Первый труд Шредера, но математической логике «Круг операций логического исчисления»¹ вышел в Лейпцинге в 1877 г.^[20][21] В этой работе он, в частности, впервые сформулировал принцип двойственности. Итоги своим исследованиям в этой области он подвел в трехтомнике «Лекции по алгебре логики (точная логика)»^[22]. Третий том озаглавлен «Алгебра и логика отношений» (Algebra und logik der relative) и содержит весьма обстоятельное изложение исчисления отношений. Шредер исследовал также общие свойства исчислений и на этом пути получил вариант системы, теперь называемой теорией квазигрупп.

Одной из центральных задач алгебры логики Шредер, как и другие специалисты в этой области, считал решение логических уравнений. Именно этой проблематики его исследований мы и коснемся. Всякое равенство Шредер приводит к виду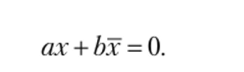

Это возможно, так как любое равенство у = z эквивалентно равенству yz+yz = 0, разложение левой части которого по конституентам относительно х, у, z дает результат.

т.е. равенство вида ах + Ьх = 0.

Среди равенств этого вида Шредер различает «аналитические», или тождественно истинные, например хх + хх = 0, и «синтетические», или истинные только при некоторых х. Аналитические равенства не могли быть, по Шредеру, уравнениями, поскольку уравнение рассматривалось им как условие, которому должен удовлетворять х, т. е. подстановка х должна обращать эго уравнение в тождество. Решить уравнение, по Шредеру, значит, во-первых, выяснить, имеет ли оно решение, т. е. выяснить — существуют ли такие выражения, которые, будучи подставлены на место х в уравнение, обращают его в тождество. И если такие выражения существуют, то надо найти какую-нибудь общую форму, из которой могли бы быть получены все решения уравнения (1.6). На первый из этих вопросов отвечает результат исключения х из уравнения (1.6), или резольвента аЪ = 0, представляющая, как отмечал еще Буль (см. выше), необходимое и достаточное условие разрешимости уравнения (1.6), общая форма решения имеет вид.

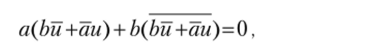
при любом значении и (сравните с решением Венна). Если условие ab = О удовлетворено, то подстановка д = Ьй+аи обращает уравнение (1.6) в следующее:

т.е. в уравнение вида.

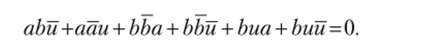
Если ab = 0, т. е. тождественный нуль, то получим.

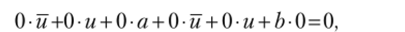
т.е. подлинное тождество. При этом существенно, что и — произвольный класс.

Наоборот, если какое-нибудь х удовлетворяет условию (1.6), то для этого же х верно и соотношение х = Ьй + аи при и = х.

Таким образом, Шредер фактически показал, что для всякого х равенство.

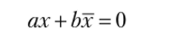
равносильно тому, что выполняется ab = 0: найдется такой класс и, что х = = Ьй+аи.

Утверждение о существовании такого и, что х, определяемый равенством (1.7), удовлетворяет уравнению (1.6), эквивалентно утверждению о том, что любое и, удовлетворяющее равенству (1.7), дает и решение уравнения (1.6).

Решить уравнение (1.6), по Шредеру, таким образом, эквивалентно тому, чтобы заменить это уравнение парой условий: ab = 0 и «найдется такой класс и, что х = Ьй + аи».

Разумеется, соотношение (1.7) есть при этом логическое следствие из уравнения (1.6), только если (1.7) берется вместе с утверждением существования и хотя, наоборот, при всяком и соотношение (1.6) есть логическое следствие из (1.7).

Важную роль в развитии алгебры логики, а также в распространении ее идей в России сыграл выдающийся русский ученый Платон Сергеевич Порецкий (1846—1907). Сын военного врача, П. С. Порецкий в 1870 г. окончил физико-математический факультет Харьковского университета, специализируясь по астрономии. С 1867 г. он начал работать в качестве астронома-наблюдателя при Казанском университете, где впоследствии защитил докторскую диссертацию по астрономии (1886) и читал лекции по астрономии и математике. Здесь же П. С. Порецкий прочел первый в России курс математической логики. С 1881 по 1904 г. выходит цикл его работ, посвященный проблемам алгебры логики. Мы остановимся лишь на некоторых аспектах его исследований в этой области, изложенных в первой изданной им большой работе^[23], которая послужила основой упомянутого курса читанных им лекций. Поскольку последующие его работы главным образом только систематизировали и развивали идеи этой работы или же в какой-то мере относились к исчислению высказываний, мы их оставим в стороне.

П. С. Порецкий понимает логическое уравнение не в качестве условия, которому надо удовлетворить. Он рассматривает его в качестве посылки, из которой требуется вывести логические следствия, все или некоторые определенного вида. В соответствии с этим у него получается другое определение того, что значит решить логическое уравнение.

Посылку, заданную равенством вида х = у, П. С. Порецкий приводит к форме.

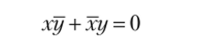
и называет логической единицей посылки. Произведение логических единиц посылок считает логической единицей задачи и обозначает через М (х, у, 2, …). Сумму логических нулей посылок он называет логическим нулем задачи и обозначает через N (x> у, 2, …).И таким образом формулирует способ решения задачи: для определения некоторого класса х через остальные достаточно умножить этот класс на функцию, которая получается из логической единицы задачи подстановкой 1 вместо определяемого класса и 0 вместо дополнения этого класса:

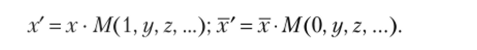
Из второго равенства по законам де Моргана х' =х + М (0, г/, 2,…), и, следовательно, для х^/ получаются два выражения.

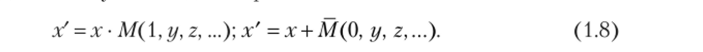
Эти два выражения для х? Порецкий называет полным решением, потому что «отрывочные сведения, предлагаемые нами в посылках, могут быть сконцентрированы в двух простых формулах, предназначенных к тому, чтобы изобразить полную картину той роли, которую играет каждый данный класс»¹. Далее Порецкий задается вопросом, нельзя ли охарактеризовать класс od', используя не все сведения, имеющиеся в посылках и относящиеся и к другим классам, а употребив лишь сведения, касающиеся самого класса х?. Такой характеристикой класса У будет решение.

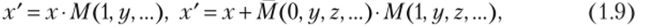
названное Порецким точным решением.

Как уже упоминалось, под решением уравнения П. С. Порецкий понимал вывод следствий из исходной информации. Точное решение уравнения (1.9) получается отбрасыванием некоторых слагаемых, равных нулю. Иногда считают, что оно получается методом исключения сведений. В своей «Алгебре логики», в которой как бы подводился итог работам по алгебре логики XIX в. и которая была написана под сильным влиянием идей Порецкого, Л. Кутюра писал: «В логике различие терминов известных и неизвестных является искусственным и почти бесполезным: все термины в сущности известны, и речь идет только о том, чтобы из данных между ними соотношений вывести новые соотношения (т.е. отношения неизвестные или неявно известные). Такова цель метода Порецкого…»^[24][25]

• [1] 2 Morgan Л. de. Formal logic, or the calculus of inference, necessary and probable. London, 1847.
• [2] Минто В. Дедуктивная и индуктивная логика. М., 1896. С. 48.
• [3] Смысл оператора скобки «)» соответствует слову «каждый»; его работа проясняетсяниже.
• [4] 2 Де Морган использовал для такого составного имени запись «Р, Q».
• [5] См.: Morgan A. de. Formal logic… Ch. 6.
• [6] Boole G. The mathematical analysis of logic, being an essay towards a calculus of deductivereasoning. Cambridge, 1847.
• [7] Boole G. An investigation of the laws of thought, on which are founded the mathematicaltheories of logic and probability. London, 1854.
• [8] Boole G. The mathematical analysis of logic. P. 3.
• [9] Boole G. On the conditions by which the solution of questions in the theory of probabilitiesare limited // Philosophical Magazine. 1854. Vol. 8. № 4. P. 91—98.
• [10] См.: Чебышев П. Л. Избранные труды. M.: Изд-во АН СССР, 1953. С. 220.
• [11] Следует иметь в виду, что Буль не строит свою систему в виде исчисления в современном смысле: он не отделяет постулируемые свойства операции от выводимых.
• [12] Жегалкин И. И. О технике вычисления предложений в символической логике // Матем.сб. 1927. № 34. Вып. 1.
• [13] Boole G. An investigation of the laws… P. 62.
• [14] Boole G. An investigation of the laws… P. 62.
• [15] Ibid.
• [16] Venn J. Symbolic logic. London, 1881; 2nd ed. London, 1894.
• [17] Venn J. Symbolic logic. London, 1894. P. 2.
• [18] Операция деления не является операцией в строгом смысле этого слова, ибо ее результат неоднозначен.
• [19] Schroder Е. Vorlesungen uber die Algebra der Logik (exacte Logic). Bd. 1—3. Leipzig, 1890—1905.
• [20] Schroder Е. Dcr Operationskreis des Logikkalkiils. Leipzig, 1877.
• [21] См.: Бобынин В. В. Опыты математического изложения и логики. Сочинения Эрнеста Шредера// Физико-математические науки в их настоящем и прошедшем. 1886—1894.Вып. 2. С. 65−72, 178−192, 438−458.
• [22] Schroder Е. Vorlesungen uber die Algebra der Logik (exacte Logic). Bd. 1—3. Leipzig, 1890—1905.
• [23] Порецкий П. С. О способах решения логических равенств и об обратном способе математической логики. Казань, 1884.
• [24] Порецкий П. С. Указ. соч. С. 65.
• [25] Couturat L. L’algebre de la logique. Paris, 1905.