Элементы теории графов

В коммерческой деятельности коммерсантам постоянно приходится решать задачи поиска покупателей продукции, товаров, имеющихся в распоряжении у предприятий, клиентов-посредников как на территории России, так и за рубежом. При этом в движении постоянно находятся люди, деньги, товары, документы, информация. Так, например, после определения руководителем возможных мест, которые необходимо посетить, возникает задача выбора оптимального маршрута из имеющихся, так называемая задача коммивояжера, которая представлена графически на рис. 4.2.

Граф G — это совокупность двух конечных множеств вершин X и множества пар вершин U (рис. 4.2). При этом элементы множества U могут повторяться, а также могут повторяться элементы в парах. Граф, заданный на множествах X и U, обозначается G = (X, U). Если элементы в парах множе;

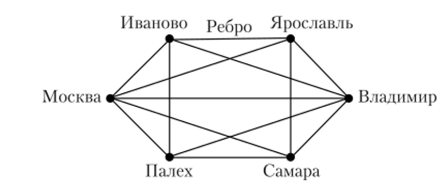
Рис. 4.2.

ства U не упорядочены, то граф называется неориентированным, в противном случае — ориентированным, или орграфом.

Элементы множества X называют вершинами графа, а множества U — ребрами для неориентированного графа и дугами для орграфа. На плоскости граф задается в виде точек (вершин) и линий, соединяющих некоторые из них (ребер или дуг). На рис. 4.3, 4.4 изображены соответственно неориентированный (несвязный) и ориентированный графы.

Для неориентированного графа на рис. 4.3 множество вершин X и ребер U можно записать так:

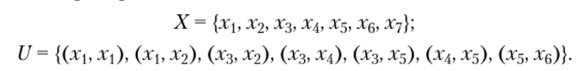
Для ориентированного графа множества вершин и дуг записываются следующим образом:

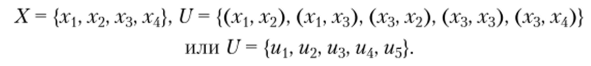
1. Приведем ряд определений для неориентированных графов. Ребро, начало и конец которого совпадают, называется петлей (x_hx_{) (рис. 4.3).

Вершины называются смежными, или соседними, если существует ребро, их соединяющее — (рс, х₂), (дг₃, х₄), (х₃, х₅), (х₄, х$), (х₅, х_б), вершины х% и х$ — несмежные.

Если вершина является началом или концом ребра, то вершина и ребро называются инцидентными.

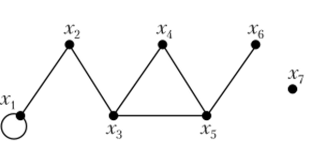
Рис. 4.3.

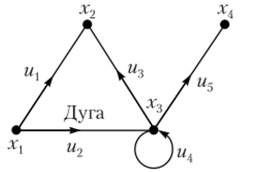
Рис. 4.4.

Степенью вершины называется число инцидентных ей ребер, степень вершины х обозначается d (x). Например (см. рис. 4.3), d (x₂) = 2; d (x₃) = 3; d (x₄) = 2; d (x^) = 3. Вершина, степень которой равна нулю (d (x₇) = 0), называется изолированной (х₇). Вершина, степень которой равна единице (<7(х₆) = 1), называется висячей, или тупиковой (х_б).

Теорема 1. В графе сумма степеней всех его вершин число четное, равное удвоенному числу ребер графа.

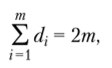
где i — число вершин; т — число ребер.

Теорема 2. Число вершин нечетной степени любого графа четно или равно нулю (теорема Эйлера о рукопожатиях).

Последовательность вершин и ребер, в которой конец предыдущего ребра совпадает с началом следующего, называется маршрутом. Число ребер в маршруте определяет его длину: (ху; х₂; х₃; х_Г); х₄; х₃; х₂) — маршрут, длина которого равна 6 (см. рис. 4.3).

Цепью называется маршрут, в котором все ребра различны. Например (х₄; х₃; х₂; x_f) — цепь, длина которой равна 4. Простой называется цепь, в которой все вершины различны, например (х₄, х₂, х₃, х₄, х₃) (см. рис. 4.3).

Граф называется связным, если для любых двух его вершин существует цепь, соединяющая эти вершины. Граф, представленный на рис. 4.2, — связный, а на рис. 4.3 — несвязный, поскольку не существует цепи, соединяющей вершину х₇ с остальными.

Расстоянием между вершинами связного графа называется длина самой короткой цепи, соединяющей вершины.

Диаметром графа называется максимальное расстояние между его вершинами.

Циклом (простым циклом) называется цепь (простая цепь), начало и конец которой совпадают, на рис. 4.3 это последовательность (х₃, х₄, х₅; х₃).

Цикл в графе называется эйлеровым, если он содержит все ребра графа ровно один раз. Связный граф, в котором есть эйлеров цикл, называется эйлеровым графом. Его можно нарисовать, не отрывая карандаш от бумаги и не повторяя линий, одним росчерком (рис. 4.7, б).

Теорема 3. Связный граф называется эйлеровым тогда и только тогда, когда степень каждой его вершины четная.

Подграфом графа G называется граф G_{ с множеством вершин Х и множеством ребер U такой, что Х_х е X, U е U. Для графа на рис. 4.3 подграфом может быть граф G_x = (Х> t/_t), где Х_х = (x_hx₂, x₃, x₄, x₅), a U_{ = {(х_ьх₂), (х₂, х₃), (х₃, х₄), (х₃, х₅)}.

Компонентой связности графа называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа данного графа, на рис. 4.3 граф имеет две компоненты связности.

Вершина графа, удаление которой повышает число компонент связности, называется точкой сочленения. Под удалением вершины понимается удаление самой вершины и всех инцидентных ей ребер. Точкой сочленения является, например, вершина х₃ (см. рис. 4.3), удаление которой приводит к появлению третьей компоненты связности.

Деревом называется связный граф без циклов (рис. 4.5).

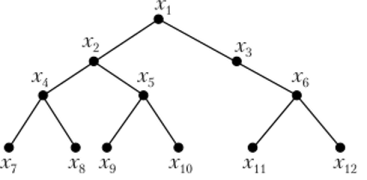
Рис. 4.5.

Вершина Х — корень дерева. Лесом называется граф без циклов, представляющий собой совокупность деревьев (рис. 4.6).

Граф называется полным, если любые две его вершины соединены ребром (см. рис. 4.2).

Граф называется плоским, если ребра пересекаются только в вершинах.

Граф называется регулярным степени d, если все его вершины имеют степень d. На рис. 4.2 изображен регулярный граф степени d = 5.

Регулярный граф, все вершины которого имеют степень 1, называется паросочетанием. Граф называется двухдольным,.

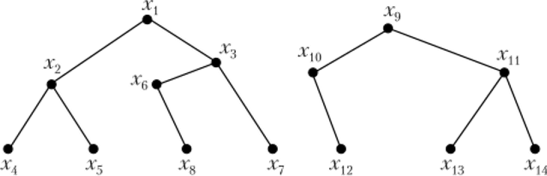
Рис. 4.6.

если множество его вершин X может быть разделено на два непересекающихся подмножества Y и Z таким образом, что каждое ребро графа соединяет вершины из двух разных подмножеств Y и Z.

Гамильтоновой цепью называется простая цепь, содержащая все вершины графа ровно один раз. Например, для графа (рис. 4.7, а) цепь (6,1,5,4,3, 2,8, 9,10, 11,12,13,14,15, 20, 19, 18, 17, 16, 7) является гамильтоновой.

Гамильтоновым циклом называется гамильтонова цепь, начало и конец которой совпадают. Если в конец предыдущей цепи дописать вершину 6, получим гамильтонов цикл.

Граф называется гамильтоновым, если в нем имеется гамильтонов цикл (см. рис. 4.7, а).

Теорема4. Если в графе Gen вершинами степень каждой вершины не меньше чем п/2, то граф G — гамильтонов.

Термин «гамильтонов» связан с именем ирландского математика У. Гамильтона, который в 1859 г. предложил игру «Кругосветное путешествие». Каждой из 20 вершин додекаэдра (см. рис. 4.7, а) соответствует один из городов мира. Необходимо, переезжая из города в город по ребрам додекаэдра, посетить каждый город только один раз и вернуться назад. Эта задача сводится к поиску простого цикла, проходящего через каждую вершину графа.

Задачи, касающиеся эйлеровых и гамильтоновых цепей и циклов, часто встречаются на практике. Например, стоимость выполнения всего комплекса коммерческих операций или работ существенно зависит от последовательности, в которой они выполняются.

Рис. 4.7.

а — гамильтонов граф; б — эйлеров граф.

Граф называется взвешенным, если каждому его ребру поставлено в соответствие некоторое число, называемое весом ребра, например расстояние между городами, стоимость или время проезда между ними.

Задачу коммивояжера можно представить в виде как ориентированного, так и неориентированного графа (рис. 4.8, а, б).

Предложенный вариант решения задачи коммивояжера представляет собой кольцевой маршрут, где каждый город посещается только один раз, начиная с любого населенного пункта.

2. Для ориентированных графов в основном все определения сохраняются, однако имеются некоторые отличия. Последовательность дуг, в которой конец предыдущей дуги совпадает с началом следующей, называется путем. Длина пути определяется количеством в нем дуг. Путь называется простым, если в нем дуга не встречается дважды, в противном случае он является составным. Путь, в котором никакая вершина не встречается дважды, называется элементарным. Путь, который начинается и заканчивается в одной и той же вершине, называется контуром.

В неориентированном графе пользуются термином не путь, а цепь, а вместо контура — цикл.

В графе на рис. 4.4 путем является, например, последовательность (хх₃, Х2). Последовательность {рс₂ х₃; Х4) путем не является, так как не существует дуги, соединяющей х₂ и х₃.

Для ориентированного графа вместо степени вершины вводится понятие полустепеней исхода и захода. Если вершина является началом дуги, то дуга называется исходящей из вершины, если концом, то — заходящей. Полустепенью исхода вершины d~(x) называется число дуг, исходящих из этой вершины, полустепенью захода d⁺(x) — число дуг, заходя;

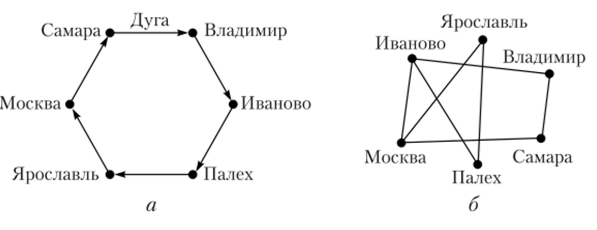
Рис. 4.8.

а — ориентированный — контур; 6 — неориентированный — цикл щих в вершину. Для графа, изображенного на рис. 4.4, можно записать.

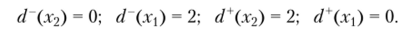
При решении задач на компьютере граф лучше представлять в виде матриц, операции с которыми удобно проводить на компьютере.

Известно несколько типов матриц, позволяющих задавать граф: смежности, инциденции, пропускных способностей.

Матрица смежности вершин графа представляет собой квадратную матрицу Л_11Х «> строки и столбцы которой соответствуют вершинам, каждый элемент которой а,-, определяется следующим образом:

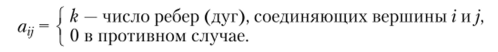
Для ориентированного графа элемент а, у равен числу дуг, направленных от вершины i к вершине j.

Для неориентированного графа, представленного на рис. 4.3, матрица смежности симметрична и имеет размерность 7×7 и записывается в виде.

Слева и сверху проставлены номера вершин.

Для ориентированного графа, изображенного на рис. 4.9, матрица смежности тоже квадратная (6×6) и записывается в виде.

Матрицу смежности чаще применяют для задания неориентированного графа. Для задания ориентированного графа лучше использовать матрицу инцидеиций.

Матрицей инциденций ориентированного графа с п вершинами и т дугами называется матрица В с п строками и т столбцами, элемент которой определяется следующим образом:

Для неориентированного графа элемент Ь" = 1, если вершина инцидентна ребру, и 0 в противном случае.

Для ориентированного графа, представленного на рис. 4.9, матрица инциденций В имеет следующий вид:

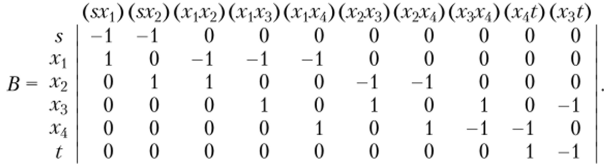
Конечный граф без циклов и петель, ориентированный в одном направлении от входа к выходу графа, называется сетью.

Взвешенный ориентированный граф без петель, в котором выделено k вершин, называемых полюсами, является^{-полюсной} цепыо. Среди сетей особо выделяется двухполюсная транспортная сеть (см. рис. 4.9) S = (N, II) с множеством вершин ЛГи множеством дуг U, для которых выполняются следующие условия:

• 1) существует только одна вершина сети s е N, в которую не заходит ни одна дуга. Эта вершина называется входом, или истоком, сети;
• 2) существует только одна вершина сети t е N, из которой не выходит ни одной дуги сети. Эта вершина называется выходом, или стоком, сети;

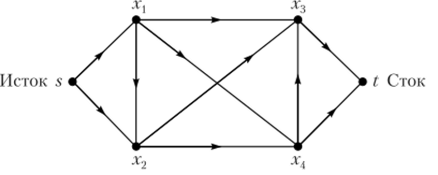
Рис. 4.9

3) каждой дуге сети и е U поставлено в соответствие неотрицательное число с (и), называемое пропускной способностью дуги.

Примерами вершин сети могут быть пересечения автострад, электростанции, телефонные узлы, железнодорожные узлы, аэропорты, водохранилища, товарные склады.

Примерами дуг сети могут быть дороги, линии электропередачи, телефонные линии, авиалинии, водные магистрали, нефтеи газопроводы.

Постановку и решение подобных задач можно получить с помощью методов сетевого моделирования.