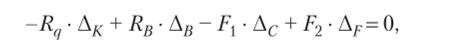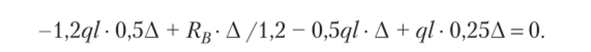Принцип возможных перемещений

Принцип возможных перемещений (принцип Лагранжа) является одним из основных положений теоретической механики, рассматривающей абсолютно твердые недеформируемые тела.

Суть принципа возможных перемещений состоит в следующем: для того, чтобы система, имеющая идеальные связи, находилась в равновесии, необходимо и достаточно, чтобы сумма элементарных работ всех приложенных к ней сил на любой совокупности возможных перемещений равнялась нулю.

Принцип Лагранжа может быть использован в задачах статики при определении реакций в связях вместо уравнений равновесия.

Применение принципа Лагранжа поясним наследующем примере.

Рассмотрим двухпролетную шарнирно-консольную балку (рис. 12.3, а), загруженную распределенной нагрузкой q и силами F, F>. Поставим задачу определить реакцию R_B. Для этого удалим связь В и по ее направлению зададим любое возможное перемещение Д_в(рис. 12.3, б). Поскольку после удаления связи балка превратилась в механизм с одной степенью свободы, построить схему изменения этого механизма не представляет трудности, полагая заданное перемещение малым. В результате все точки балки, кроме опорных, получили перемещения.

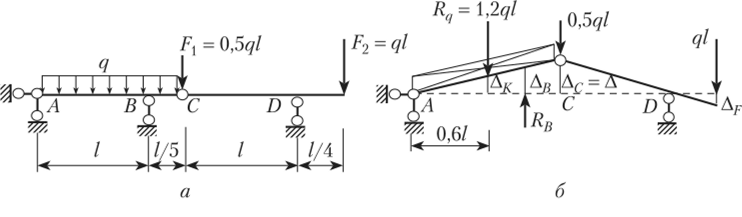
Рис. 12.3.

Для полученной схемы механизма применим принцип возможных перемещений, т. е. составим сумму возможных работ для всех сил, точки приложения которых получили перемещения:

где R_(/ = 1,2q — равнодействующая распределенной нагрузки; Д^ — перемещение точки приложения равнодействующей распределенной нагрузки.

Все указанные перемещения выразим через одно, например Д_с, введя общий множитель: А_с = Д, А_в = Д/1,2, А_к = 0,5Д, Д^ = 0,25Д.

Уравнение работ после подстановки значений перемещений и заданной нагрузки примет вид.

Сократив все члены полученного выражения на Д, определим, что R_B = = 1,02ql. Знак «плюс» означает, что принятое направление опорной реакции R_B правильное.

Принцип возможных перемещений применим при расчете не только абсолютно твердых тел. Он может быть распространен и на упругие тела, если в сумме возможных работ учесть и работу внутренних сил (12.13).

Тогда в применении к упругим деформируемым системам принцип возможных перемещений можно сформулировать следующим образом: если упругая деформируемая система под действием приложенных к ней внешних сил находится в равновесии, то при всяком возможном бесконечно малом перемещении точек этой системы сумма работ се внешних и внутренних сил равна нулю.

Приведенная формулировка принципа возможных перемещений приводит к тому же результату, что и закон сохранения энергии, т. е. к формуле (12.15).