Решение комбинаторных задач, соответствующих специфике профессиональной деятельности

Одна из трудно поддающихся осмыслению ситуаций связана с использованием часто встречающейся в практике формы «хотя бы сколько-то из имеющихся». Рассмотрим вариант рассуждений при решении соответствующих задач.

Пример 5.9.

Для участия в игре по станциям надо сформировать команду из шести учащихся. В команде должны быть хотя бы два певца и хотя бы три художника. В курируемом классе учатся три учащихся из музыкальной школы и четыре учащихся из художественного училища. Решено было составлять команду только из певцов и художников. Решение

Чтобы осмыслить возможные элементарные комбинации ситуации «хотя бы … из …», можно использовать табличку из шести столбцов по числу членов команды. В каждой строке этой таблицы две ячейки должны быть заполнены певцами, а три ячейки — художниками:

Оставшаяся одна ячейка может принадлежать учащемуся с любым талантом: певцу или художнику. Следовательно, в таблице должно быть две строки. Необходимо будет обсчитать две элементарные ситуации, каждая из которых удовлетворяет условию задачи, а значит, они соединяются союзом или: {п, п, п, х, х, х} или {п, п, х, х, х, х}.

Внутри каждой из этих ситуаций певцы и художники соединяются союзом и, гак как в любом случае по условию задачи выбран должен быть набор из шести элементов: {п, п, п} и {х, х, х}} или^[1].

Условию задачи будет соответствовать краткая вербальная формулировка следующего вида.

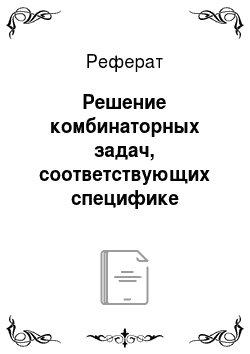
Этап 1. «Выбрать три певца из трех певцов и три художника из четырех художников или два певца из трех певцов и четыре художника из четырех художников».

Перевод краткой вербальной формулировки на язык математических символов должен учитывать, что внутри выбранных подмножеств певцов и художников не предполагается по условию задачи распределение каких-либо функций. Они равноправны между собой, а значит, упорядоченность в комбинациях не предполагается. Используем основные формулы комбинаторики для подсчета числа комбинаций (табл. 5.2) правила комбинаторики (табл. 5.1).

Этап 2.

Получаем следующую математическую модель условия задачи:

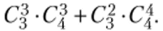
Преобразование внутри математической модели обычно вызывает наименьшие трудности, но в данном случае стоит обратить внимание на вычисление С|. Безусловно, надо понимать, что даже с точки зрения здравого смысла три элемента из грех имеющихся без учета порядка можно взять только один раз, или число неупорядоченных трехэлементных подмножеств множества из трех элементов равно одному. Если формально использовать формулу для подсчета числа сочетаний С|, то хоть и длинным путем, но получим тот же результат, преодолев смущение при вычислении 0!, который по определению равен 1, а не 0, как некоторые пытаются изобразить. Сокращая одинаковые множители и заменяя 0! = 1 и 1! = 1, получаем:

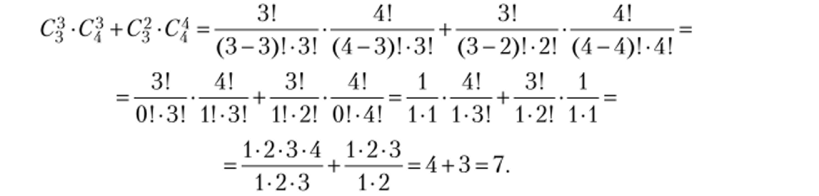
Ответ. Надо обдумать возможность и рациональность семи вариантов составления команды.

С трудностями обработки информации и математических вычислений встречаются некоторые студенты при решении задачи, в которой неизвестно количество элементов в исходном множестве.

Пример 5.10.

Учитель задумал использовать на занятиях методику работы в парах сменного состава. При выбранном варианте методики учащиеся должны встретиться в паре только один раз, и каждый учащийся до начала занятий должен быть подготовлен по одной, независимой от других, порции учебного материала, зафиксированКаждая пара будет работать в среднем 5 + 5 = 10 мин.

ной в карточке. При этом каждый учащийся должен получить по каждой карточке индивидуальные объяснения, ответить на контрольные вопросы или решить аналогичную задачу, его самостоятельную работу должны проконтролировать. После этого он должен объяснить свою карточку соседу, записать необходимую информацию ему в тетрадь и проконтролировать самостоятельную работу соседа по своей карточке. Первый раз первым учащимся карточки объясняет учитель. Достоинством методики является многократное объяснение своей карточки разным партнерам, что способствует углубленному пониманию материала. Методика требует больших временных затрат на подготовку и проведение этой работы. Учитель может рассчитывать на сдвоенный урок. В классе учатся 20 человек. Будем считать, что для выбранной темы учащийся должен затратить в среднем на работу с одной карточкой 5 мин. Сколько разных карточек должен подготовить учитель? Сколько учащихся он должен подготовить по каждой карточке до начала занятий?

Решение

Два урока длятся 45 + 45 = 90 мин.

За 90 мин можно провести несколько сеансов работы в парах, после которых пары меняются, а именно 90: 10 = 9 сеансов.

Если работой в парах охватываются п человек, то за один сеанс можно соста;

п о п _п п 9п

вить — пар. За 9 сеансов могут успеть овладеть карточками друг друга 9 — = — пар.

Поскольку пары встречаются между собой один раз, то в списке пар не будет таких, которые отличаются друг от друга только порядком записи фамилий в паре, г. е. упорядоченности внутри пар, но условию задачи не требуется. Это означает, что о п ^п-

количество пар равно количеству сочетании из п человек, но 2: Li =-.

^{1 1 я} (/? — 2)! • 2!

Дано:

я = ?;

т = 2;

порядок: нет.

Требуется выяснить, из скольких учащихся можно составить — сочетаний по два учащихся.

Математическая модель заданной ситуации представляет собой уравнение.

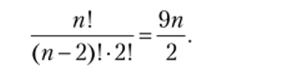
Распишем п по определению факториала через произведение (п — 2) первых последовательных натуральных чисел: п = (п - 2)!? (п — 1) • п и произведем сокращение в левой части уравнения на одинаковые множители:

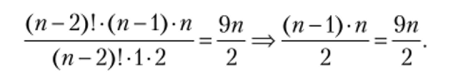
Умножим обе части уравнения на 2 и раскроем скобки: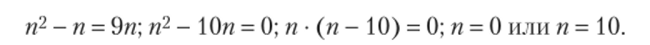

Значение п = 0 нас не устраивает в качестве решения, так как п — это количество учащихся, с которыми мы собираемся работать. Значит, решением уравнение является п = 10.

Заметим, что условие пф 0 можно было применить и раньше, сократив обе части уравнения на п и решая уже линейное, а не квадратное уравнение:

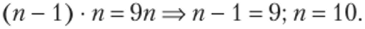
При любом варианте преобразования математической модели значение неизвестного п равно 10, т. е. 10 человек можно успеть охватить работой в парах сменного состава по указанной методике за сдвоенный урок.

Однако в классе 20 человек. Следовательно, учителю придется разделить класс на две группы и самому подготовить для первоначального ввода по два человека по каждой из 10 карточек.

Вывод. Не для всякой темы можно использовать данную методику, методика трудоемка, но результат того стоит.

Еще один тип задач, часто встречающихся в методиках разных областей знаний, — это задачи на определение рисков, шансов, т. е. на определение вероятностей некоторых событий.

Оценка вероятности осуществления равновозможных и имеющих конечное число исходов событий подразумевает использование классической формулы вероятности. Обычно классическая формула вероятности приводится в следующем виде:

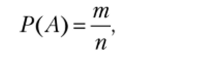
где п — число всевозможных исходов некоторого эксперимента; т — число благоприятных исходов эксперимента.

Однако часто встречаются ошибки при использовании этой формулы, связанные с тем, что студенты меняют местами числитель и знаменатель дроби, путают, что на что делится при вычислении вероятностей. Затруднения возникают и при решении вероятностных задач с использованием формул комбинаторики, где одинаковые буквы тип обозначают разные величины.

Провоцирует эти ошибки еще и то, что сначала обычно описываются в условии всевозможные исходы эксперимента и лишь потом в вопросе задачи оговариваются благоприятные исходы, а в формулу подставить подсчитанные соответствующие значения надо в обратном порядке. Эти печальные прецеденты позволяют предложить другой вариант записи формулы классической вероятности через русские буквы и мнемоническое правило ее запоминания. Число благоприятных исходов эксперимента обозначим буквой б, а число всевозможных исходов некоторого эксперимента — буквой в. Поскольку читаем мы обычно в направлении сверху вниз, то и легко запоминается расстановка букв в формуле в порядке алфавита сверху вниз:

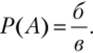
Количество исходов эксперимента совпадает часто с количеством способов выбора, что подсчитывается при помощи формул комбинаторики.

Пример 5.11.

Индивидуализация и объективность контроля достижений учащихся, столь популярная в последнее время, подразумевает случайность выбора конкретных заданий для конкретного учащегося, независимость этого выбора от воли экзаменатора. Одна из компьютерных программ организации контроля предполагает случайный выбор контролирующих задании из заложенной базы задании для составления конкретного варианта теста. Пусть в базе имеются восемь типовых заданий и 12 заданий повышенной сложности. В каждом варианте теста должно быть восемь разных заданий. Какова вероятность того, что в случайно выбранном варианте окажется ровно три типовых задания, обеспечивающих испытуемому получение удовлетворительной отметки? Решение

Оценка вероятности осуществления описанной ситуации подразумевает использование классической формулы вероятности, так как события, о которых идет речь в задаче, равновозможны и имеют конечное число исходов.

Подсчитаем сначала количество всевозможных исходов описываемой ситуации. Чтобы избежать путаницы с общими и благоприятными исходами, не будем пока рассматривать вопрос задачи. Краткая вербальная формулировка всего того, о чем говорится до вопроса, сводится к следующей фразе: «Выбрать восемь заданий из двадцати заданий». Теперь запишем полное условие общей ситуации при помощи математических символов, как это делалось при решении комбинаторных задач.

Дано: п = 20; т = 8;

порядок: нет. повтор: нет;

Полученное число соответствует количеству всевозможных исходов: в = 125 970. Теперь разберемся с благоприятными исходами, которые оговариваются в вопросе задачи. Представим себе этот выбранный вариант теста. В нем восемь заданий. Кричать «Ура!» по поводу благоприятного исхода будем тогда, когда из восми заданий варианта три задания окажутся типовыми. А какими будут остальные задания? Интерпретируем благоприятную ситуацию в виде таблички из восьми ячеек:

Краткая вербальная формулировка благоприятной ситуации: «Выбрать три типовых из … типовых и пять сложных из … сложных».

Запишем символическое условие для выбора типовых заданий.

Дано: п = 8; т = 3;

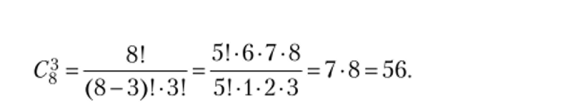
порядок: нет;

Запишем символическое условие для выбора сложных заданий. Дано: п= 12; т = 5;

порядок: нет;

Вспоминаем правила комбинаторики и роль союза и в краткой вербальной формулировке и получаем количество благоприятных исходов указанной ситуации:

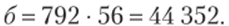
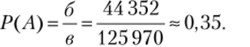
Ответ: 0,35.

Удовлетворит ли такой ответ организаторов контроля? Достаточно ли, чтобы лишь в трети случаев вариант удовлетворял запросам экзаменаторов? Как можно изменить формулировку вопроса, чтобы смягчить требование? На сколько при этом скорректируются результаты? Можно еще много вопросов поставить, но это уже проблемы педагогики. Математика же, в частности комбинаторика, ответила, как она может обработать вопросы, поставленные перед ней.

На основании вышеизложенного можно сделать следующие выводы.

При обработке информации часто возникает необходимость подсчета количества способов выполнить некоторые действия, в частности действия по составлению комбинаций из некоторых элементов.

Комбинации могут быть наделены разными свойствами, которые надо абстрагировать по трем существенным для комбинаторики параметрам:

• 1. Равно ли количества элементов в исходном множестве и в составляемом подмножестве?
• 2. Составляемые подмножества могут отличаться друг от друга по порядку записи элементов?
• 3. Могут ли в составляемых подмножествах повторяться элементы?

Для правильного ответа на эти вопросы надо прежде всего перевести информацию с естественного языка на математический. Эту операцию бывает полезно выполнять в два этапа:

• 1. Краткая словесная (вербальная) формулировка условия.
• 2. Полная запись условия на языке математических символов.

Для вербальной обработки текста с целью решения комбинаторных задач предлагается следующая заготовка: «Выбрать… (…) из … (…) и (или) … (…) из …(…).», где наименование элементов множества и подмножества, которым оставлено место в скобках в краткой вербальной форме, должны совпадать.

Для символьной обработки текста с целью решения комбинаторных задач предлагается следующая заготовка.

Дано:

п =…;

т =…;

порядок: да/нет;

повтор: да/нет.

Для выбора математической модели, адекватной описываемой ситуации, можно использовать табл. 5.3.

Трудности обработки информации имеют отношение к замечательному свойству математики ум в порядок приводить, выделять главное и «раскладывать по полочкам», разделяя сложное действие на элементарные составляющие его операции.

• [1] п, п} и {х, х, х, х