Сложное движение твердого тела. 
Пара вращений

Рассмотрим две системы координат — неподвижную и подвижную Су_ху^уз (рис. 9). Твердое тело, с которым связана система координат PxiXjXj, движется относительно подвижной системы координат Су_хУ2Уу Требуется описать распределение скоростей точек твердого тела в абсолютном движении, т. е. в движении относительно неподвижной системы координат 0?,?₂4з;

Рис. 9 Рис. 10.

Радиус-вектор точки М

где ортогональные операторы Г₍, Г₂ задают преобразования от системы координат Су, У2)>3 к 0^₂^₃ и Px_tx₂x_} к Су₁у₂у₂ соответственно Векторы R_w, R_c заданы в системе вектор г^^,) — в системе Су₁у₂у₂, а вектор г_м⁽²⁾ — в системе Px_ix₂x_y Продифференцируем равенство (8.1) и получим.

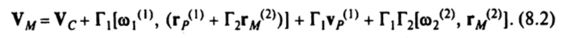
Здесь<0|^(,) х г*¹* = Г,'¹ Г/⁴, ю₂^<2) х г*²⁾ = ly’I^r®, а>|^(|), в>₂^<2) — переносная и относительная угловые скорости. Далее Г|v_P^ = = Г, г/^|> = Vр_г — относительная скорость точки Р в системе Су₁у₂у₂, V_c+ г,!©,⁰¹, г/¹¹] = У_Ре — переносная скорость точки Р Оставшиеся слагаемые в формуле (8.2) представляются в виде.

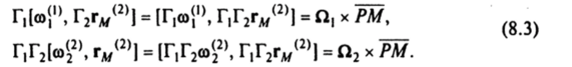
Угловая скорость О, =0, — переносная угловая скорость, П₂ = П, — относительная угловая скорость твердого тела. Формула (8 2) с учетом (8.3) представляется в виде.

С другой стороны, по формуле Эйлера в абсолютном движении _м = _р +О_а х РМ, где П" — абсолютная угловая скорость твердого тела в системе координат 0^₂?зСравнение этих двух выражений приводит к равенствам зз Полученный результат сформулируем в виде теоремы: если твердое тело движется в системе координат, которая в свою очередь перемещается относительно неподвижной системы координат, то абсолютная скорость полюса (точка Р твердого тела) находится как сумма переносной и относительной скоростей, а абсолютная угловая скорость — как сумма переносной и относительной угловых скоростей.

0.8.1. Сложное движение твердого тела называется парой вращений, если У_с= 0, V_/v= 0, С1_е = -П_г.

В этом случае согласно (8.4) У М — У Ре = П, хСЯ, т. е. все точки твердого тела имеют одинаковую скорость и, значит, тело совершаетмгновенно-поступательное движение. Величина скорости Р_ехСР называется моментом пары вращений. Если условия в определении (8.1) выполняются во все время движения, то тело совершает поступательное движение. Очевидно и обратное утверждение: всякое поступательное движение твердого тела можно представить как сложное движение с помощью подходящей пары вращений.

Из теоремы о сложении движений вытекает следствие: всякое движение твердого тела складывается из поступательного переносного движения и относительного движения — вращения тела вокруг начала подвижной системы координат. В самом деле, пусть начало подвижной системы координат точка С совпадает с точкой Р твердого тела, а оси Су, Су₂, Су₃ параллельны во все время движения соответствующим осям неподвижной системы координат 04,^зТогда _Pr = O_i Q* = Q, =0. Переносная скорость точки М V, = У_р, а относительная V_r = Q_rx РМ _у т. е. соотношение _м = _р +Clx РМ (формула Эйлера) выражает теорему сложения движений.