Работа силы. 
Потенциальные силовые поля. 
Теорема об изменении кинетической энергии. 
Закон сохранения энергии

Пусть г = г (/) — закон движения материальной точки, F — сила, действующая на точку, a dr = rdt — действительное перемещение.

0.4.1. Элементарной работой силы на действительном переме;

з щении называется дифференциальная форма dA = Fdr = .

1*1.

Если материальная точка в процессе движения по траектории переместилась из положения Р₀ в положение Р, то работа силы на этом перемещении представляется криволинейным интегралом (рис. 15)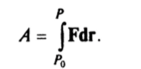

• 0.4.2. Если в каждой точке области D трехмерного евклидова пространства задан вектор силы F (r, t), то говорят, что в области D задано силовое поле.
• 0.4.3. Силовое поле называется потенциальным, если существует

я я силовая функция V(г, t) и F = V_rC/(г, /), где V_r = -г—е, + ——е₂ +.

OX I OXj

я.

дх

— е₃ — оператор градиента по пространственным координатам.

з.

0.4.4. Стационарное потенциальное силовое поле называется консервативным. В этом случае силовая функция не зависит от времени.

Важным свойством силовых полей является независимость работы от пути, соединяющего две фиксированные точки области D. Сформулируем известную теорему анализа о независимости криволинейного интеграла от пути интегрирования: если силовое поле, заданное в односвязной области Д является стационарным.

rsTf

(~- = 0) и безвихревым (rot F = 0), то оно консервативно, и работа ot ^

силы при перемещении из точки г₀ в точку Р зависит только от этих точек и не зависит от пути, их соединяющего. Из условия.

дХ дХ

rot F = 0 следуют условия Коши —— = -г—^L, к, / = 1, 2, 3, полного.

OX_t иХ_к

дифференциала выражения Fdr. Здесь функции Х_ь Х₂, Х_ъ> зависящие от х, х₂, х₃, — компоненты вектора F. При вычислении работы получим.

П. Рассмотрим силовые поля на плоскости Оху, порождаемые силовыми функциями U_x = ф и U₂ = -г~ где (г, <�р) — полярные координаты. Силовые поля F_k = V_rU_k®, г = (х, у), к=, 2, определены на всей плоскости Оху, за исключением начала координат, и консервативны. Если из плоскости Оху исключить луч, соединяющий начало координат с бесконечно удаленной точкой, то в полученной односвязной области D работа сил не будет зависеть от путей, соединяющих две фиксированные точки. Однако это становится неверным для первого силового поля, если рассматривать всю плоскость с выколотым началом координат. Рассмотрим в качестве пути замкнутый контур — единичную окружность S_{ = = {(х, у): х = cos ф, у = sin <�р, 0 < <�р? 2л}. Тогда в первом случае.

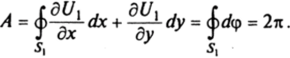
так как dr-0 вдоль контура S_v В этом случае обход начала координат не влияет на величину работы, хотя область определения силового поля неодносвязна.

0.4.5. Величина Т = ½/яг² называется кинетической энергией материальной точки.

Т. При движении материальной точки дифференциал кинетической энергии равен элементарной работе действующей на точку силы на действительном перемещении.

А Имеем.

Функция (/, многозначна, и работа силы по замкнутому контуру, охватывающему начало координат, равна 2п. Во втором случае.

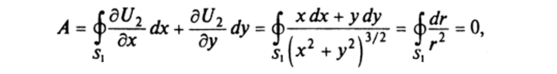
С. 1. Приращение кинетической энергии материальной точки при ее перемещении из точки Р₀ в точку Р равно работе силы на этом перемещении

где г₀, г — скорости материальной точки, соответствующие ее положениям Р₀ и Р.

С. 2. Производная от кинетической энергии по времени равна мощности силы, действующей на точку, т. е.

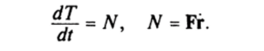
Доказательства следствий 1 и 2 очевидны.

С.З. Если силовое поле консервативно, то полная механическая энергия точки сохраняется при ее движении.

А В случае консервативного поля работа силы на пути Р₀Рравна разности U (t) — U (г₀), где U (г) — силовая функция, а г₀, г — радиусы-векторы точек Р₀, Рсоответственно. Назовем потенциальной энергией консервативного силового поля величину V (v) = -U (г). Из первого следствия найдем.

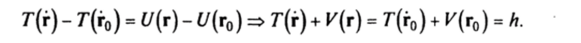
0.4.6. Сумма кинетической и потенциальной энергий называется полной механической энергией.

Таким образом, полная механическая энергия материальной точки Е= Т+ V=h постоянна вдоль траектории — закон сохранения энергии. ?

Если силовое поле консервативно и задана постоянная полной энергии А, то все траектории движения с полной энергией И расположены в области возможных движений D_h={г: U (г) -ь И > 0}.

П. 1. Рассмотрим движение материальной точки в однородном силовом поле F = -mge₃ (падение точки в пустоте). Здесь g — ускорение свободного падения, е₃ — орт вертикальной оси Ох_у Поле консервативно и его потенциальная энергия V=mgre_y Полная энергия l/2mr²+mgre₃ = И — закон сохранения энергии. Область возможных движений D_h={r: h — mgre₃? 0} — полупространство. Уравнение движения точки /яг = -/wgre₃ имеет решение г = г (0) + + v (0)/- l/2g/²e₃, где r (0), v (0) — начальные условия движения. Легко показать, что траектория движения есть парабола, расположенная в вертикальной плоскости, являющейся линейной оболочкой векторов е₃, v (0) и проходящей через точку, радиус-вектор которой равен г (0).

П. 2. Пусть материальная точка движется под действием силы F = /я/,(г)г + mf₂(г, г) г. Момент количества движения G = [г, /яг| изменяется согласно уравнению.

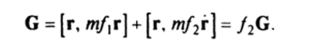
Полагая G= Ge, где G= |G| получим Ge + Ge = /₂Ge. Умножим последнее равенство скалярно на ё и, учитывая равенство ее = 0 (е — единичный вектор), найдем Се² = 0. Поскольку в случае общего положения G* 0 (если G=0, то движение происходит по прямой, проходящей через начало координат), то е = 0 и вектор е постоянен. Далее reG= 0, т. е. движение точки происходит в плоскости. Сила m/,®г консервативна, так как.

Функция/₂(г, г), если речь идет о модели сил сопротивления, противоположных скорости точки, отрицательна, и полная энергия Е убывает, когда г*0. Область возможных движений D_h = = {г: U® + h? 0} в зависимости от вида силовой функции G® представляется либо шаром, либо объединением шаровых слоев.