Динамика точки. 
Теоретическая механика

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ЗАКОНЫ ДИНАМИКИ

Аксиоматическое построение динамических механических моделей базируется на основных понятиях и законах механики. Выше были даны определения механической системы и ее движения, но ничего не сказано о причинах, вызывающих движение. Во второй главе предполагалось, что движение механических систем задано, и изучались его свойства. В динамике речь пойдет о причинах, вызывающих движение, и об определении движения, когда эти причины известны. Сформулируем ряд постулатов и определений, на которых базируется механика.

Материальные точки взаимодействуют друг с другом. Это взаимодействие служит причиной движения и моделируется силами.

• 0.1.1. Сила есть векторная величина, описывающая взаимодействие материальных точек. Говорят, что сила приложена к материальной точке.
• 0.1.2. Все множество материальных точек в ?³ называется Вселенной.
• 0.1.3. Материальная точка называется изолированной, если можно пренебречь ее взаимодействием с остальными точками Вселенной.

Первый закон динамики (закон инерции Галилея). В пространстве ?³ существует система координат S, относительно которой всякая изолированная материальная точка находится в покое или в состоянии равномерного прямолинейного движения.

• 0.1.4. Система координат S называется инерциальной.
• 0.1.5. Системой отсчета в механике называется система координат S в ?³ и система координат на числовой оси времени.

Т. Система координат S_]y движущаяся поступательно с постоянной скоростью относительно инерциальной системы координат S, является инерциальной системой координат.

А Рассмотрим изолированную материальную точку М. Закон ее движения в инерциальной системе координат Sимеет вид R = Rq +.

+ V₀/, где t e R' и Ro-V₀ — постоянные векторы. Начало системы координат 5, (точка О,) движется относительно системы координат S по закону 00 = А + Вt и справедливо равенство R = А + В/ + Гг (г), где Г — постоянный ортогональный оператор, определяющий ориентацию репера относительно репера S (рис. 13).

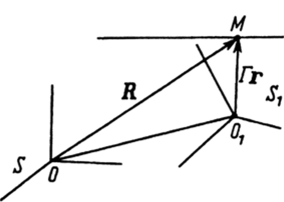
Отсюда находим.

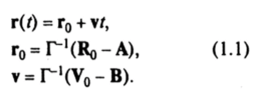
Из равенства (1.1) следует, Р_ИС и что изолированная точка М

движется равномерно и прямолинейно относительно системы координат 5|, а значит, система координат 5, инерциальна. Т С. 1. Для любой изолированной материальной точки найдется такая инерциальная система координат, в которой эта точка покоится и совпадает с началом системы координат.

Согласно (1.1) достаточно выбрать В = V₀ и, А = R^.

С. 2. Инерциальные системы отсчета образуют галилееву группу размерности 10.

В самом деле, для задания инерциальной системы отсчета нужно задать: а) /₀ е Л¹ — новое начало отсчета времени на числовой оси; б) А, В е ?³ — движение начала новой инерциальной системы координат 5i; в) Г е SO (3) — ориентацию осей системы координат S относительно инерциальной системы координат S.

С.З. Ускорение материальной точки относительно инерциальной системы координат инвариантно относительно галилеевой группы.

? Законы движения материальной точки в двух инерциальных системах отсчета связаны соотношениями.

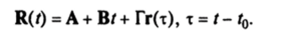
Отсюда после двукратного дифференцирования по времени получим.

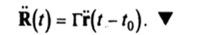
Во второй главе неоднократно рассматривались два типа систем координат — подвижные и неподвижные. Опыт познания материи свидетельствует о том, что во Вселенной не существует абсолютно неподвижных объектов, с которыми можно было бы связать неподвижную систему координат, поскольку все материальные объекты движутся друг относительно друга. В дальнейшем под неподвижной системой координат будем понимать инерциальную систему координат. На практике всякую систему отсчета связывают с тем или иным материальным объектом. В частности, в качестве инерциальной системы координат выбирают систему координат с началом в центре масс Солнечной системы (точка внутри Солнца) и с осями, направленными на звезды (система Коперника). Как показывает опыт, эта система координат с большой степенью точности является инерциальной, т. е. всякая «изолированная» материальная точка движется относительно этой системы координат «почти по прямой с постоянной скоростью».

Второй закон динамики (Ньютон). Ускорение материальной точки относительно инерциальной системы координат прямо пропорционально силе, приложенной к точке, и обратно пропорционально ее массе, т. е.

где F — вектор силы, т — масса точки, w — ускорение точки.

В «Математических началах натуральной философии» (1687 г.) И. Ньютон сформулировал этот закон так: «изменение движения пропорционально приложенной силе и происходит в направлении силы», понимая под этим равенство ^-(mv) = F.

И. Ньютон сделал ко второму закону примечание: если на материальную точку действуют две силы, то ее ускорение будет равно геометрической сумме ускорений, вызванных действием каждой силы по отдельности (закон параллелограмма сил). Другими словами, если w, = /w^_,F,, w₂ = т~^]F₂, то w = w, + w₂, и поскольку w = m" ¹ F, to F = F, + F₂. Здесь F, F₂ — действующие на точку силы, w, w₂ — вызываемые ими ускорения, a w, F — результирующие ускорение и сила соответственно.

Третий закон динамики (Ньютон). Силы, описывающие взаимодействие двух точек, равны по величине, направлены по прямой, соединяющей точки, и противоположны, т. е. F|2 = «^21 = ХЛ/, Л/₂, где F,₂ — сила, действующая на первую точку со стороны второй, a F₂, — сила, действующая на вторую точку со стороны первой.

С. 4. Величины ускорений взаимодействующих материальных точек обратно пропорциональны их массам. Имеем

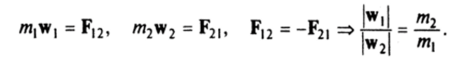
В динамике рассматривают две основные задачи: первая — определение закона движения по заданным силам, вторая — определение по заданному закону движения действующей на точку силы. Решение первой задачи возможно, когда внешние силы заданы, например, как функция времени, координат и скоростей материальной точки, т. е. F = F (/, г, г). В этом случае соотношение (1.2) представляет собой систему обыкновенных дифференциальных уравнений г = m^_1F (f, г, г), и речь идет об отыскании его общего решения г = г (Г, г (0), г (0)), где г (0), г (0) — начальные условия движения. Для отыскания общего решения могут быть использованы методы теории обыкновенных дифференциальных уравнений. Описанная модель не единственна. В механике встречаются также такие модели, когда сила зависит от всей предыстории движения точки, например,.

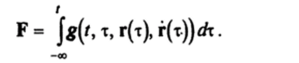
Соответствующие уравнения движения имеют интегродифференциальный вид.

Вторая основная задача, задача определения силы rio заданному движению, имеет два аспекта. Если задано движение г = г (/), то сила отыскивается путем двукратного дифференцирования по времени и использованию соотношения (1.2). Если же задано семейство движений г = г (/, С|,…, с₆), с_{9…, с₆ — произвольные параметры, и имеется соглашение о модели сил, например, F = F (f, г, г)* то определение силы как функции времени, координат и скоростей сводится к задаче обращения функций.

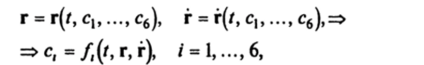
на основе теоремы о неявной функции. Далее сила определяется из второго закона Ньютона в виде.

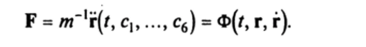
Масса есть мера инерции материальной точки, т. е. ее склонности сохранять равномерное и прямолинейное движение относительно инерциальной системы координат. Чем больше масса точки, тем большую необходимо приложить к ней силу для придания ей определенного ускорения. Следствие из третьего закона динамики позволяет по измерениям ускорений устанавливать отношения масс тел к выбранной эталонной массе.

В настоящем курсе классической механики предполагается, что взаимодействие материальных точек обусловливается только их взаимным расположением и взаимными скоростями в данный момент времени.

Все величины, используемые в механике, размерны. В качестве основных величин принимаются: длина — размерность метр [м], время — размерность секунда [с] и масса — размерность килограмм [кг]. Производные величины измеряются в следующих единицах: скорость — [мс^_|], ускорение — [мс~²], сила — [кгмс'²]. Сила в 1 кгмс'² называется ньютоном [н].