Схемы счета до заданного числа

Выше было показано, как можно строить счетчики, емкость которых задана и оказывается меньшей, чем число его двоичных разрядов. Соответствующий скачок числа, записанного в счетчике, может быть постоянным, определяемым схемными соединениями данного счетчика, а может быть и переменным, если речь идет о счетчике с параллельным вводом. Однако на практике бывает необходимо сравнивать два непрерывно изменяющихся числа, изображаемых параллельными кодами. Такова, например, задача числового программного управления координатными перемещениями, когда необходимо сравнивать число, изображающее заданное перемещение какого-либо органа станка, с числом, отражающим с необходимой точностью фактическое перемещение этого органа. Такое сопоставление выполняется устройствами, называемыми цифровыми блоками сравнения или компараторами.

Устройства, осуществляющие сравнение двух чисел А и В, имеют следующие три разновидности:

• • установление соотношения А — В или А Ф В
• • установление соотношения А > В или А < В
• • установление соотношения А > В, А = В или А < В.

Первый тип компаратора представляет собой так называемую комбинационную схему, поразрядно проверяющую условия логической равнозначности. Комбинационной эту схему можно назвать потому, что ее выходное дискретное значение однозначно определяется комбинацией состояния ее входов в момент сравнения. Два числа, А и В, будут, равны между собой только в том случае, когда все их разряды между собой совпадают. Поэтому для выработки сигнала об общем равенстве сравниваемых чисел достаточно выработать сигналы о совпадении (равнозначности) для каждой пары разрядов и осуществить конъюнкцию этих сигналов поразрядного совпадения. Поразрядное совпадение сравниваемых чисел А и В означает, что у обоих чисел оба значения данного к-го разряда равны между собой, т. е. а_к = Ь_к = 0 или же а_к = b_K= 1. Это есть не что иное, как инверсия арифметического сложения или сложения по модулю 2.

Второй тип компаратора является частным случаем третьего типа.

Третий тип компаратора реализует такую методику, при которой результаты сравнения в разрядах, имеющих больший вес, т. е. в старших разрядах, делают ненужным дальнейшее сравнение в младших разрядах, поскольку результат сравнения чисел А и В уже предрешен.

Принципиально компараторы можно строить двумя способами:

• • параллельным, когда оба сравниваемых числа вводятся в компаратор полностью и операция сравнения внутри компаратора производится над обоими числами целиком;
• • последовательным, когда сравниваемые числа вводятся в компаратор поразрядно попарно, начиная со старшего либо с младшего разряда.

Параллельный компаратор реализуется из одинаковых поразрядных ячеек без запоминания результатов сравнения каждого разряда. Это, однако, не исключает запоминания общего результата сравнения двух чисел в целом, но это делается уже вне компаратора.

В принципе для представления трех результатов сравнения двух чисел А и В достаточно (причем с избытком) и двух шин и У_у Например, если А> В, то ^К₂=10; если А < В, то Y_tY₂ = 01 и, наконец, если А = В, то К, У₂ = 00 или Y_lY₂^ss 11. Однако на практике при построении различных схем автоматики, например следящих координатных или других подобных приводов, оказывается удобным иметь три выхода компаратора: Y₂

и Y_y Если А > В, то Y_x = 1, У₂ = 0 и = 0; если А < В, то Y_y = 0, У₂ = 0 и Т₃ = 1; наконец, если А = В, то Y_l=Y_i = 0 и Y₂= 1. Такие выходы по трем шинам удобно использовать для релейного отключения исполнительного сервопривода в случае равенства А и В и для включения этого сервопривода на полную скорость в прямом или обратном направлении в зависимости от того, А > В или, наоборот, В > А.

В каждом к-ом разряде можно считать, что.

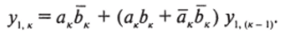
Это выражение следует понимать таким образом, что выход у, данного, к-го, разряда будет равен 1, если в данном разряде а_к = 1, а Ь_к = 0, либо, если а_к = Ь_кУ будь то а_к = Ь_к= 1 или а_к = Ь_к = 0, он будет равен выходу у, предыдущего младшего разряда, т. е. у₁._к = у,_(к__|).

Аналогично (симметрично) можно записать:

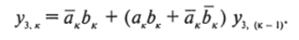
Соответственно.

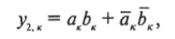
т. е. выход у_2к данного, к-го разряда будет равен 1 только, если в данном разряде а_к = Ь_кУ будь то а_к = b_K = 1 или а_к = Ь_к = 0. Если ^ак*Ь_КУ то либо у_1я, либо у_и будут равны 1, а у_2к будет равен 0.

Структурная схема такой ячейки поразрядного сравнения приведена на рис. 9.10.

На этой схеме прямоугольником со значком V обозначен элемент дизъюнкции на два входа (элемент «ИЛИ»), прямоугольником со значком & обозначен элемент конъюнкции на два входа (элемент «И»), а прямоугольником с кружочком на выходе обозначен инвертирующий элемент. Нетрудно убедиться,.

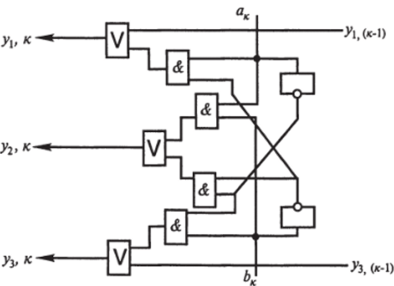
Рис. 9.10. Структурная схема ячейки компаратора.

что изображенная на рис. 9.10 структурная схема соответствует логическим соотношениям, приведенным выше.