ДИССИПАЦИЯ ЭНЕРГИИ при движении ЖИДКОСТИ. 
УРАВНЕНИЯ НАВЬЕ-СТОКСА

Простейшая модель диссипативных сил была рассмотрена в теории малых колебаний (см. гл. 7), когда соответствующие обобщенные силы порождаются квадратичной диссипативной функцией Релея. Аналогичная модель рассеяния энергии, хорошо согласующаяся с экспериментом, может быть построена в случае движения баротропной жидкости.

Изменение расстояний между точками элементарной частицы определяется тензором скоростей деформаций (см. § 10.4).

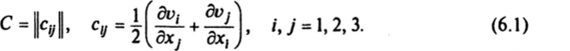
В частности, ((<�Ж)', dr) = (Cdr, dr), поскольку R = г + v (r. Г) т + … («Ж)' = dv/drdr, а точка означает дифференцирование по т и подстановку т = 0. Квадратичный по скоростям диссипативный функционал, описывающий рассеяние энергии в однородной изотропной вязкой жидкости, должен зависеть от инвариантов тензора скоростей деформаций (6.1), так как он обязан сохранять свое значение при замене исходной системы координат на систему с другой ориентацией. Инварианты тензора скоростей деформации равны.

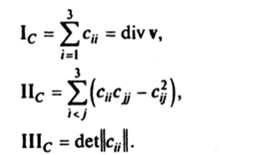
Квадратичный диссипативный функционал зададим в виде.

Здесь к, к₂ — постоянные, характеризующие вязкость жидкости, П — область, в которой рассматривается движение вязкой жидкости. Симметричный тензор скоростей деформаций С можно путем замены системы координат привести к диагональному виду diag (C|, с₂, с₃}. Подынтегральное выражение в (6.2) примет в этом случае вид ?|(С| + с₂ + с₃)² + к₂{с₁с₂ + с, с₃ + с₂с₃). Из условия положительной определенности последнего выражения по переменным С|, с₂, с₃ вытекают неравенства k_t > 0, 0 < -к₂к~¹ < 3. Функционал.

(6.2) представим в форме.

где X, р называются коэффициентами вязкости и связаны с постоянными k_t, к₂ равенствами X = 2k_t + к₂, 2р = -к₂. Заметим, что функционалы (6.2) и (6.3) аналогичны квадратичным функционалам потенциальной энергии в теории упругости малых деформаций (см. § 9.2). Работа диссипативных сил на возможных перемещениях представляется вариацией.

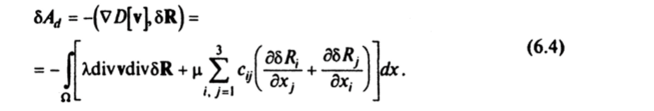
Если в выражении (6.4) вектор возможных перемещений 8R заменить на вектор действительных перемещений dR = dt, то с учетом квадратичности функционала (6.3) получим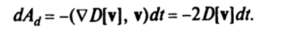

Следовательно, вязкие силы рассеивают в единицу времени мощность — 7D[y.

Вариацию (6.4) добавим в левую часть принципа Д’Аламбера— Лагранжа (2.2) и получим.

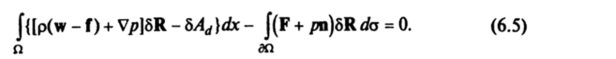
Вариацию (6.4) преобразуем с использованием формулы Остроградского—Гаусса (преобразования аналогичны произведенным в § 9.3). Имеем.

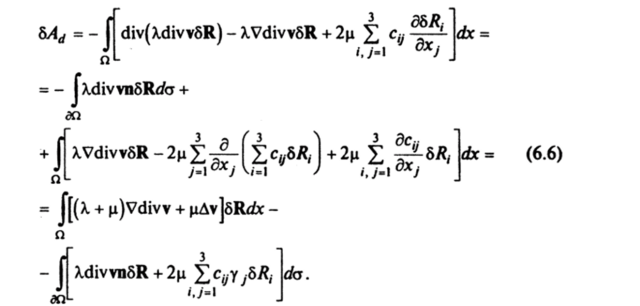
Здесь у, у₂, уз — компоненты внешней нормали п к поверхности дП. При преобразованиях в (6.4) учитывалось равенство.

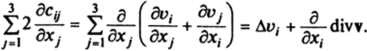
Вариационный принцип (6.5) с учетом равенства (6.6) принимает вид.

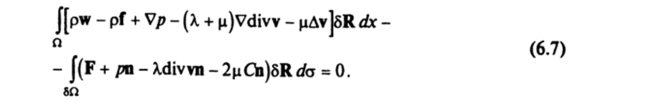
Поскольку вариация 6R произвольна, то из (6.7) согласно основной лемме вариационного исчисления получим уравнения Навье—Стокса.

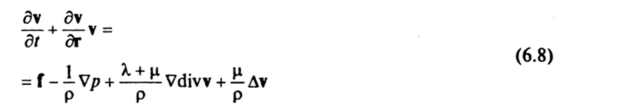
и граничные условия.

если вариация 6R на поверхности дО. также произвольна (свободная поверхность). Если вязкая жидкость движется внутри фиксированной области П, то на ее границе дО принимаются обычно граничные условия: v (r, /) = 0 на 5П и соответственно 6R = О на 5Q.

Правая часть равенства (6.9) представима в виде Ли, где Р= = II ЛуII — симметричный тензор напряжений с компонентами.

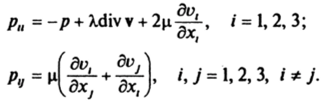
Для несжимаемой жидкости div v = 0, плотность р постоянна, а уравнения Навье—Стокса принимают вид.

где v = цр^_| — кинематический коэффициент вязкости. Отметим, что свойство вязкости несжимаемой жидкости характеризуется одним параметром.

Уравнения Навье—Стокса (6.8) совместно с уравнением состояния р = Ф (р) и уравнением неразрывности.

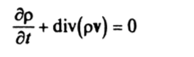
образуют полную систему нелинейных дифференциальных уравнений в частных производных, описывающую движение баротропной вязкой жидкости. Точное интегрирование этих уравнений удается лишь в редких случаях.

так как при у= И давление должно совпадать с р₀. Это следует из граничных условий (6.9), которые принимают вид.

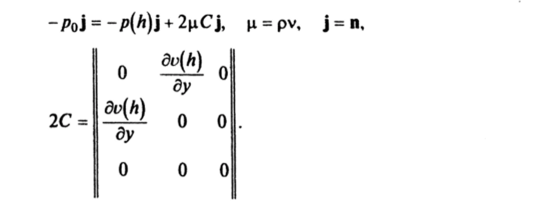
П. В качестве примера рассмотрим установившееся движение вязкой несжимаемой жидкости по наклонной плоскости в поле силы тяжести (рис. 69). Пусть толщина слоя жидкости равна И, а.

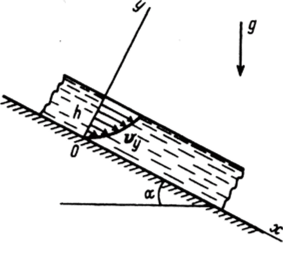
Рис. 69.

скорость v = t>(y)i, где i — орт оси Ох. Легко проверить, что уравнение неразрывности div v = 0 справедливо для выбранного поля скоростей, а уравнения Навье—Стокса (6.10) в проекциях на оси Ох л Оу принимают вид.

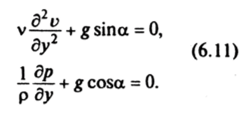
Вследствие стационарности движения давление р = р (у). На давление атмосферного воздуха уравнения (6.11) находим

свободной поверхности при y-h постоянно и равно р_а. Из второго Отсюда получаем p (h) = р₀ и dv (h)/dy = 0. Первое уравнение системы (6.11) имеет решение.

удовлетворяющее условию dv (h)/dy= 0.

Вычислим количество жидкости, протекающей через сечение, ортогональное оси Ох и имеющее по оси Oz единичный размер. Имеем.

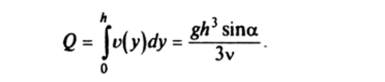
Найденное решение задачи описывает ламинарное течение жидкости и реализуется экспериментально при малых значениях безразмерного параметра R = u₀hv~^l (число Рейнольдса), где и₀ = = Qh~^] — среднее значение скорости жидкости. Экспериментальная реализация найденного решения свидетельствует об его устойчивости. При увеличении числа Рейнольдса ламинарное течение становится неустойчивым, и движение жидкости приобретает турбулентный характер, когда траектории отдельных частиц имеют сложный хаотический характер. Математическая теория турбулентных движений выходит за рамки данного курса теоретической механики.