Метод термодинамических потенциалов

Термодинамические исследования физических явлений могут быть осуществлены при помощи двух методов: метода циклов и метода термодинамических потенциалов. Первым возник метод циклов или круговых процессов. Его использовали в своих исследованиях еще Карно, Клаузиус и др. Суть этого метода заключается в том, что для установления какой-либо закономерности определенного явления подбирается подходящий обратимый цикл и к этому циклу применяются уравнения первого и второго начал термодинамики. Чаще всего используется цикл Карно. Слабостью метода циклов является то, что всякий раз приходится подбирать подходящий цикл, а сам его выбор произволен [5].

Сейчас при исследованиях термодинамических свойств систем применяется, главным образом, метод термодинамических потенциалов, предложенный Дж. Гиббсом. Основу метода составляет определение с помощью основного уравнения термодинамики (2.13) некоторых функций состояния в зависимости от выбора независимых переменных. Посредством этих функций и их производных могут быть явно выражены термодинамические свойства системы. При этом первые производные определяют термические свойства, а вторые — калорические.

Термодинамическими потенциалами называют такие функции от соответствующих параметров, определяющих состояние системы, с помощью которых можно вычислить полезную работу (за вычетом работы против внешнего давления) в равновесном процессе при заданных условиях. Какая именно функция будет играть роль термодинамического потенциала, зависит от условий, при которых находится рассматриваемая система.

Пусть мы хотим определить полезную работу 8^=5W-p-dV (работу, за вычетом работы расширения). Тогда, согласно (2.1) и (2.13),.

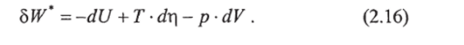
Зададимся вопросом, при каких условиях левая часть уравнения будет полным дифференциалом.

Здесь возможны несколько комбинаций, но чаще всего в термодинамике используются четыре из них:

1. Переменные объем V и энтропия д При заданных V и т] из (2.16) сразу вытекает, что 5 fV=-dU. Это означает, что при изохорно-адиабатических процессах работа совершается за счет убыли внутренней энергии. Отсюда следует, что при постоянных V и т] внутренняя энергия является термодинамическим потенциалом U=U (V, r).

Полный дифференциал внутренней энергии равен.

Отсюда следует, что изменение температуры при адиабатическом расширении равно изменению давления при изохорном сообщении теплоты системе с обратным знаком. Установление связей типа (2.19) — основа метода термодинамических потенциалов.

Функция состояния U=U (V, x) как термодинамический потенциал мало пригодна в практических исследованиях, так как одна из независимых переменных, энтропия г|, не может быть непосредственно измерена.

2. Переменные температура Т и объем V Преобразуем правую часть уравнения (2.16) таким образом, чтобы в него входили дифференциалы dTudV.

Для этого в правую часть (2.16) прибавим и из нее же вычтем дифференциал d (Tr) (последний раскроем)^[1]:

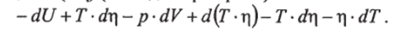
Тогда уравнение (2.16) примет вид:

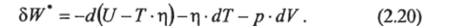aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">

При T=const и V=const

т. е. выражение F (T, V) = UТ- т| при заданных температуре и объеме является термодинамическим потенциалом и называется свободной энергией ши энергией Гельмгольца.

Из (2.22) следует (вспомним определение полного дифференциала):

Если 8^=0 (равновесная система находится только под всесторонним давлением), то из (2.20) получим:

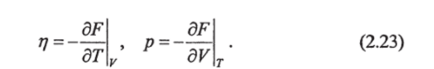
. д²Г

Вторые производные от функции F вида позволяют получить уравнение:

Из (2.24) следует, что изменение энтропии при ее изотермическом расширении равно изменению давления при изохорном нагревании.

Свободная энергия при изотермических процессах играет роль внутренней энергии при адиабатических процессах. Как видно из (2.21), при изотермических процессах работа совершается системой не за счет убыли внутренней энергии U, а за счет убыли функции F. Величина Т-г называется связанной энергией. Связанная энергия — это часть внутренней энергии системы, которая не может быть передана в форме работы в изотермическом процессе, т. е. она является «обесцененной».

3. Переменные температура Т и давление р Для перехода к переменным Т и р из правой части выражения (2.16) вычтем и к ней же прибавим дифференциал d (pV) (последний раскроем), а член Tdr перепишем как Т? di = d (T r)-r-dT. Тогда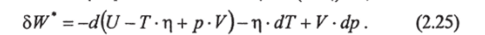

При заданных Тир получим: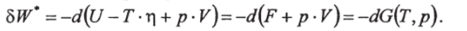

Отсюда следует, что при изотермо-изобарических процессах работа совершается не за счет убыли внутренней энергии U, а за счет убыли функции G.

Функция состояния G (T, p)=UТ-г + р? V называется термодинамическим потенциалом Гиббса или энергией Гиббса. Эта функция имеет важное значение, так как она определяется через легко измеряемые параметры Тир.

Если bfV=0, то из (2.25) следует:

Из (2.26) вытекает:

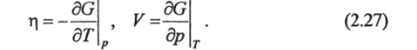
Вторые производные функции G{Tp) поТир дают уравнение.

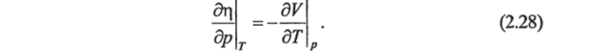
4. Переменные цир

Для перехода к переменным ц и р из правой части выражения (2.16) вычтем и к ней же прибавим дифференциал d (p-V) (последний раскроем). Получим:

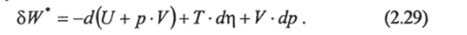
При г=const и p=const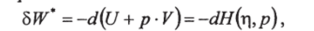

т. е. при изобаро-адиабатических процессах работа совершается за счет убыли функции H (r, p) = U + р — V. Эта функция называется энтальпией и является термодинамическим потенциалом при заданных тир.

При 51^=0 из (2.29) следует:

Из (2.30) вытекает:

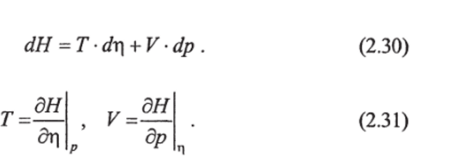
Перекрестное дифференцирование (2.31) и приравнивание вторых производных дают.

Из (2.9) и (2.30) видно, что при изобарических процессах энтальпия равна поглощенному количеству теплоты:

где С_п = — - теплоемкость при постоянном давлении. По этой ^р dT

причине энтальпию называют также тепловой функцией или теплосодержанием.

Любой из термодинамических потенциалов можно определить через другие. Так, зависимость внутренней энергии от свободной энергии можно получить из определения энергии Гельмгольца F{T, V) = U-Т-Х] и уравнения (2.23):

Связь энтальпии с потенциалом Гиббса можно установить с помощью оппелелений потенциала Гиббса и энтальпии.

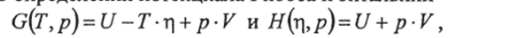
а также уравнений (2.27):

Уравнения (2.34) и (2.35), устанавливающие связь между различными термодинамическими потенциалами, называются уравнениями Гиббса-Гельмгольца.

Отметим, что в рамках этого подхода нельзя найти явные выражения для термодинамических потенциалов. Однако начала термодинамики позволяют найти связи одних свойств систем с другими их свойствами типа (2.19), (2.24), (2.28), (2.32). Такие соотношения называются основными уравнениями или соотношениями Максвелла. Другие подобные соотношения легко могут быть получены на основании применения якобианов (см. раздел 2.5).

Таким образом, все термодинамические потенциалы являются однозначными функциями состояния, причем их убыль при соответствующих условиях определяет работу системы против действующих на нее сил.

Все термодинамические потенциалы обладают аддитивными свойствами. В случае однокомпонентной системы при изменении числа молей N в некоторое число раз величины термодинамических потенциалов изменяются во столько же раз. Следовательно, аддитивная термодинамическая величина является однородной функцией первого порядка относительно аддитивных переменных¹⁰. Отсюда следует, что.

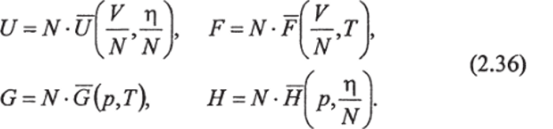
Черта сверху означает соответствующую функцию состояния на один моль вещества.

Заметим, что параметры р и Т не делятся на N, т. к. они не зависят от числа молей (т. е. от массы).

• [1] Подобные преобразования называются преобразованиями Лежандра.