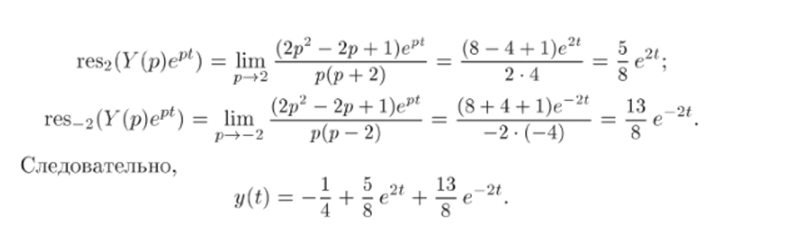Практикум. 
Теория функций комплексного переменного и операционное исчисление

Разбор типовых задач

1. Задачи к главе I. Комплексные числа и действия над ними.

Задача 33.1. Число (/3 — г)⁷ представить в алгебраической форме.

Р е ш е н и е. Напомним, что алгебраической (декартовой) формой комплексного числа называется выражение z — х 4- гу.

1) Представим число 2 = /3 — i в тригонометрической форме. Для этого найдем модуль г и аргумент ip этого числа:

откуда следует, что <�р лежит в 4-й четверти. Поэтому <�р = — + 2л к,

к € Z. Можно взять любое из этих значений 9. Итак,.

2) По формуле Муавра (2.10) найдем г¹:

2тг Следовательно, ф лежит в 3-й четверти, и ф = — —- + 2тгк, к € Z.

• 2) Применим формулу (2.12); в качестве ф можно взять любое из
• 27Г

найденных значений, например ф = —Получим.

Подставляя каждое из указанных значений к, найдем искомые значения корня:

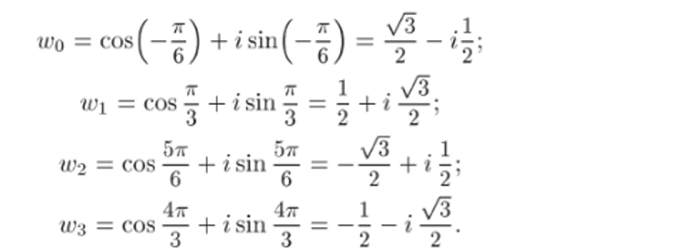
Другие значения к новых чисел ид. уже не дадут.

3 а дача 33.3. Выполнить действия над комплексными числа- ₃/(2−2г)⁴ + 72 + 4? _тт ^.

ми: —т-—"ттл—-г.— • Изобразить найденные числа на комплексной у (1 — 2*) ?+? 5 j плоскости.

Решение. 1) Число (2 — 2*), которое возводится в степень 4, представим в тригонометрической форме:

следовательно, ф лежит в 4-й четверти, и ф = -тг/4. Отсюда.

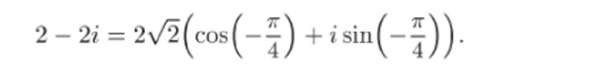
2) Выполним действия возведения в степень. Степень (2 — 2*)⁴ найдем, но формуле Муавра (2.10):

Для нахождения (1 — 2i)² удобнее применить алгебраическую формулу сокращенного умножения:

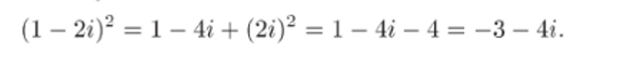
3) Выполним сложение чисел в алгебраической форме:

4) Выполним деление чисел в алгебраической форме. Для этого домножим числитель и знаменатель дроби на число, сопряженное знаменателю:

5) Извлечем кубический корень, применив формулу Муавра (2.12). Вначале представим число (-2 — 2i) в тригонометрической форме:

следовательно, <�р лежит в 3-й четверти, и = — 37г/4 (можно взять ?> = 5тг/4);

По формуле (2.12).

Так как /2у/2 = /2, то при к = О.

Рис. 57.

Найдем значения z. При t = —27 имеем z³ = —27. Для аргумента <�р числа —27 получаем cos<^ = —1, sin</? = 0. Поэтому <�р = тг, и t = -27 = 27(cos7r + isin7r). По формуле (2.12).

Итак, все корни уравнения оказались различными.

3 а д, а ч, а 33.5. Найти все решения уравнения z^x — 2z² + 4 = 0.

Р е in е н и е. Уравнение имеет четыре корня. Сделав замену переменного / = z², приходим к уравнению t² — 21 + 4 = 0. Дискриминант равен Найдем г. Для t = 1 +iy/3 получим г = |$i| = >J + 3 = 2; cosy? = = ½, sin у? = /3/2. Следовательно, у> = 7т/3, и.

Зада ч, а 33.G. Представить в алгебраической форме число Р с ш с н н е. По формуле Эйлера (2.14).

2. Задачи к главе II. Понятие функции комплексного переменного.

Рис. 58.

Задача 33.7. Изобразить множество точек z комплексной плоскости, удовлетворяющих равенству.

z — 2 + i = z + 5 — 2i.

Решение. Значение z — Zo равно расстоянию между точками z и zq. Поэтому данное равенство означает следующее: требуется найти точки г, равноудаленные от точек а = 2 — г и 6 = — 5 + 2 г. Известно, что множество точек, равноудаленных от а и Ь, представляет собой прямую, перпендикулярную отрезку аЬ и проходящую через середину с этого отрезка (т.е. срединный перпендикуляр) — рис. 58. Так как координаты середины отрезка равны полусумме соответствующих координат его концевых точек, то

Итак, искомым множеством является прямая, проходящая через точ- 3.1 ,.

ку с = — - + I — перпендикулярно отрезку ао.

Задача 33.8. Изобразить на комплексной плоскости область, заданную неравенствами |z — 2i < 2; 1 < Imz < 3.

Р е ш е н и е. Неравенство z — 2i < 2 означает, что расстояние от точки z до точки zq = 2i меньше чем 2. Поэтому множество точек 2, для которых |z — 2г| < 2, является внутренностью круга с центром 2i радиуса 2.

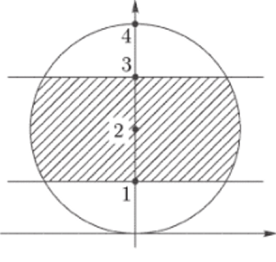
Рис. 59.

Условие 1 < Im z < 3 говорит о том, что координата у точки z заключена между 1 и 3. Множество таких точек z образует полосу, лежащую между горизонтальными прямыми у = 1 и у = 3. Искомое множество является пересечением круга и полосы, изображенным на рис. 59; граница не входит в заштрихованное множество.

Задача 33.9. Изобразить на комплексной плоскости область, заданную системой непавенсгв:

Р е ш е н и е. 1) Изобразим множество точек 2, удовлетворяющих неравенству |z — Зг| < 2, т. е. удаленных от точки 2о = 3 г на расстояние, меньшее 2. Эти точки заполняют внутренность круга с центром.

Рис. GO, а Рис. 60, б.

zo = Зг и радиусом 2 — рис. 60, а; граница круга не принадлежит множеству.

2) Неравенство равносильно соотношениям.

Точки 2, аргумент которых удовлетворяет данному условию, заполняют внутренность сектора, образованного лучами, идущими под углами 7г/3 и 2к/3 к оси ОХ — рис. 60, б.

3) Изобразим множество Imz < 4. Оно является полуплоскостью,.

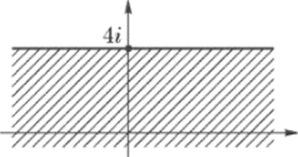
лежащей под прямой у = 4 рис. 60, в; сама эта прямая не входит в множество.

4) Искомым множеством является пересечение построенных множеств, т. е. треугольник со «скругленными» углами — рис. 60, г. Граница не входит в множество.

^Рис— ⁶⁽⁾' ⁶ 3 а д, а ч, а 33.10. Замкнутую область, изображенную на рис. 61, задать системой неравенств.

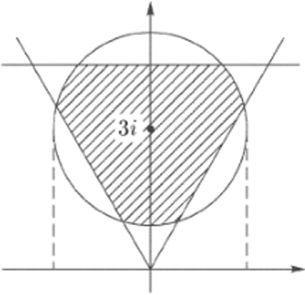
Рис. 60. г.

Рис. 61.

Р е ш е н и е. Точки указанной области лежат в замкнутом круге с центром zq = —2i радиуса 2. Поэтому они удовлетворяют неравенству |z + 2г| ^ 2. Кроме того, эти точки лежат внутри сектора с вершиной в начале координат, что накладывает условие на их аргументы. Удобно пользоваться главным значением аргумента, для которого —7г < arg 2 ^ 7 Г. Для точек данной области угол arg z отсчитывается от оси ОХ но часовой стрелке и, следовательно, является отрицательным: — Зтг/4 ^ arg. z ^ —тг/6. Итак, нужными неравенствами являются z + 2г ^ 2, -3;г/4 ^ arg г ^ -7г/6.

3. Задачи к главе III. Дифференцирование функций комплексного переменного.

Задача 33.11. Найти точки, в которых функция.

является дифференцируемой, и вычислить производную в этих точках (если таковые существуют).

Решение. Представим данную функцию w = f (z) в виде f (z) = = и (х, у) + iv (x. y). Для этого подставим z — х Лту и выделим действительную и мнимую части полученного выражения:

(мы воспользовались равенствами z = х — iy, Ini2 = у). Значит.

Согласно теореме 6.1, для дифференцируемости функции f (z) в точке г = (я, у) необходимо и достаточно, чтобы в этой точке выполнялись условия Коши-Римана (6.4). Найдем частные производные:

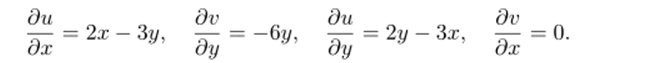
УСмЧовия (6.4) приводят к системе уравнений.

Эта система имеет единственное решение х = 0, у = 0. Итак, функция f (z) дифференцируема в единственной точке z = 0. Найдем производную /'(О). Поскольку предел в определении производной (6.1) не зависит от направления, по которому Az приближается к нулю, то можно предположить, что Az = Ах, Ау = 0. Поэтому.

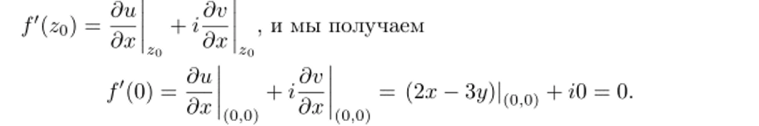
Отметим, что данная функция f (z) не является аналитической ни в одной точке, поскольку ни одна точка (включая z = 0) нс имеет окрестности, в которой функция дифференцируема.

Задача 33.12. Восстановить аналитическую функцию f (z) по ее действительной части и (х, у) = е~^у sin х + у и значению /(0) = 1.

Решение. 1) Проверим, что данная функция в самом деле является действительной частью аналитической функции. С этой.

_ д²и д²и

целью подставим и в уравнение Лапласа —=? + -г-^ = 0:

Hot'* Пи*

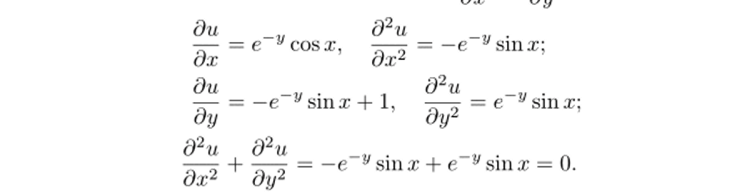
Таким образом, функция и (х, у) удовлетворяет уравнению Лапласа во всей плоскости.

2) Используя условия Коши-Римана, получаем.

• () t
• 3) Интегрируя равенство ^ = е~^у sin я — 1 по переменному т, найдем v (x, y) (при этом у считается постоянной):

где С (у) — неизвестная функция переменного у.

4) Подставим найденную функцию v (x, у) в уравнение.

и найдем С'(у):

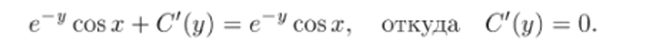
5) Проинтегрировав С (у) по у, найдем С (у):

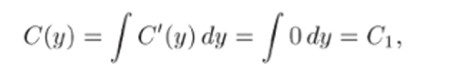
где Ci — произвольная постоянная.

6) Запишем f (z) в виде f (z) = и (я, у) + iv (х, у) и найдем Сi из условия /(0) = 1:

Окончательно получаем.

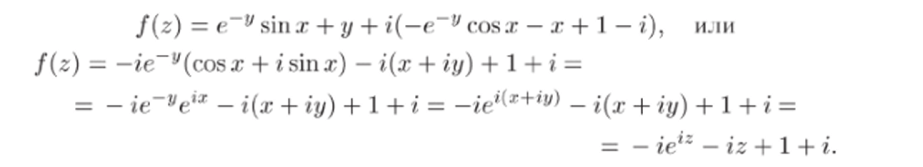
Восстановление аналитической функции по ее мнимой части проводится аналогично — см. пример 7.3.

4. Задачи к главе IV. Конформные отображения.

Задача 33.13. Найти функцию, отображающую треугольник с вершинами *4(-1.0), В (-4, -1), С (-4.1) на треугольник с вершинами А'(3,0), Б'(5, —6), С'(1,-6) (рис. 62).

Решение. Треугольник АВС можно отобразить на треугольник А’В’С' последовательным выполнением растяжения, поворота и параллельного переноса. Поэтому такое отображение реализуется линейной функцией w = az 4- 6.

1) Подберем преобразование подобия. Так как коэффициент подобия треугольников равен 2, то нужное преобразование есть W=2z. Точка Л (—1.0) перейдет в Л, (-2,0).

Рис. G2.

2) Повернем получившийся треугольник относительно начала координат на угол 7г/2 против часовой стрелки. Это преобразование запишется в виде wo =

= wie*" /*. Точка -4i (—2,0) перейдет в Л₂(0. -2).

3) Сделаем параллельный перенос получившегося треугольника на вектор А₂А' = (3,2) = 3 + 2 г. Преобразование запишется в виде w = w₂ + 3 + 2/.

Композиция указанных преобразований даст искомое отображение:

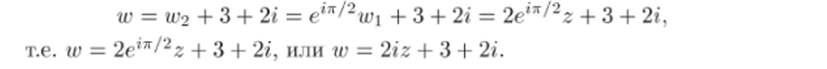
Задача 33.14. В какую область переходит круг |z + 2г| < 2 при отображении w = 1/г?

Решение. Определим вначале, во что переходит граница круга, т. е. окружность |z + 2i = 2. Согласно круговому свойству дробнолинейных отображений (теорема 9.4), эта окружность переходит в окружность (возможно, с радиусом R = оо, т. е. в прямую). Точка 2 = 0 лежит на окружности |z ?+? 2г| = 2; она переходит вш = ос. Поэтому R = ос и, следовательно, окружность z + 2г| = 2 переходит в прямую. Чтобы ее изобразить, достаточно найти две точки на этой прямой. При Z = —4i получим W = —— = 7. При z₂ = 2 — 2 г будем.

—4? 4.

иметь w₂ = -—— = - + Итак, образом окружности |z + 2i = 2 является прямая, проходящая через точки W = г/4 и w₂ = ¼ 4- г/4, т. е. горизонтальная прямая у = ¼. Поэтому образом круга z + 2i <2 будет одна из полуплоскостей (верхняя либо нижняя), ограниченная этой прямой.

Чтобы понять, какой из случаев имеет место, достаточно проверить, в какую полуплоскость отображается какая-либо внутренняя точка круга, например центр zo = —2г. Имеем w₀ = 1/zo = — l/(2i) = = г/ 2. Поскольку центр отображается в точку w₀, лежащую выше прямой у = ¼, то приходим к выводу: круг z 2г| < 2 отображается на полуплоскость 1ш z >¼.

Образ границы z + 2i = 2 можно было найти и другим способом, показанным на следующем примере.

Задач, а 33.15. В какую область переходит круг |z + i| < 3 при отображении w = 1/z?

Решение. Найдем образ окружности z + i =3. Поскольку z = = 0 не принадлежит этой окружности, то ни одна из ее точек не перейдет в W = оо. Значит, образом будет окружность конечного радиуса. Для отыскания ее центра и радиуса положим z = х 4- iy, w = и + iv и представим уравнение z + i = 3 в виде.

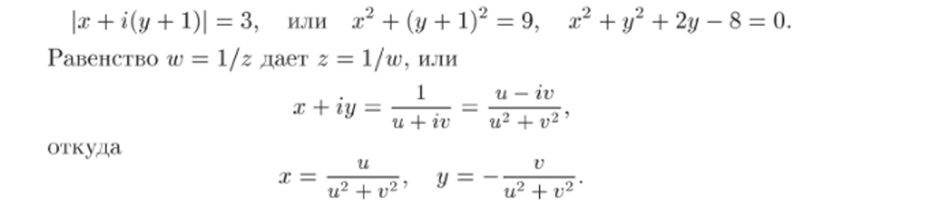
Подставим эти выражения в уравнение окружности:

Итак, окружность z 4- t| = 3 переходит в окружность с центром wq = = (0,—1/8) и радиусом R = 3/8. Точка z = 0, лежащая внутри круга |z + г| < 3, переходит в точку w = оо. Значит, при отображении w = 1/z круг |г4-г|<3 переходит во внешность круга с центром Wo = —i/8 и радиусом R = 3/8. Это множество можно задать неравенством w +1/8| > 3/8.

Задача 33.16. Найти конформное отображение w = f (z) круга |г| < 1 на круг |tu| < 1, удовлетворяющее условиям w (—i/2) = О, argw'(—i/2) = 7г/4. Указать коэффициент растяжения в точке zo — = —i/2.

Решен и е. В примере 9.8 было показано, что дробно-линейная функция, отображающая круг z < 1 на круг w < 1, имеет вид (формула (9.10)):

где Zo — точка, переходящая в точку w = 0. В нашем случае Zq = = —i/2. Осталось определить значение у?, которое найдем из условия argil/(—i/2) = тг/4:

Отсюда следует, что.

Значит, коэффициент растяжения в точке —г/2 равен 4/3, и <�р = 7г/4. Искомым отображением является функция.

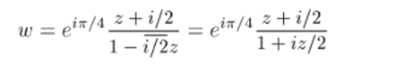
(мы использовали равенство i = —г).

Задача 33.17. Найти конформное отображение верхней полуплоскости Irn 2 > 0 на круг w < 1, удовлетворяющее условиям w (2i) = 0, argw^,(2i) = 7 г. Указать коэффициент растяжения в точке z₀ = 2г.

Решение. В примере 9.7 было показано, что конформное отображение верхней полуплоскости на единичный круг имеет вид.

Определим параметры zo и <�р. Поскольку Zo — точка, переходящая в точку w = 0, то zo = 2t. Для определения найдем w'(zq):

Поэтому.

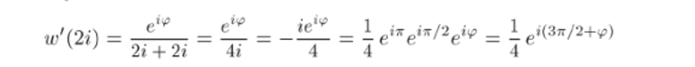
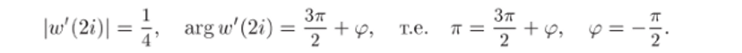
(мы использовали равенства — 1 = е*^я, i = е^1П/²). Отсюда Итак, искомое отображение дается функцией.

Коэффициент растяжения в точке 2i равен |w^#(2i)| = ¼.

Задача 33.18. Найти конформное отображение полосы, заключенной между прямыми у=х+1иу=х+3 (рис. 63), на единичный круг.

Р е ш е н и е. 1) С помощью линейной функции w = az + b отобразим данную полосу на полосу —оо < х < -foo, 0 < у < тг. Исходная.

полоса имеет ширину /2. Чтобы отобразить ее на полосу шириной тг, сделаем преобразование подобия с коэффициентом тг//2. Это преобразование задается функцией w = = 7гг//2. Точка А (—½, i/2) перейдет в.

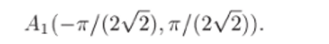
Затем повернем полученную полосу на угол 7г/4 по часовой стрелке, чтобы она стала параллельной оси ОХ. Это преобразование запишется в виде.

Точка 4j (-7r/(2/2), 7r/(2/2)) перейдет в До (0,7г/2).

Наконец, сделаем параллельный перенос на вектор А^О:

Вместо точки А (— 1 /2, г/2) можно было взять любую другую точку на прямой у = х + 1 (например, точку (0,1)). Используя равенство е^-'*/⁴ = 1/n/2 — i/V2. можно записать полученное преобразование в такой форме:

• 2) Отобразим полученную полосу на верхнюю полуплоскость lmz>0. В § 11, п. 1 было показано, что показательная функция w = е^: отображает полосу 0 < Im 2 < 7 г на верхнюю полуплоскость. Поэтому нужным преобразованием будет w. = е^и'³.
• 3) Отобразим верхнюю полуплоскость на единичный круг с помощью дробно-линейного отображения w = e^1lf -——, I11120 > 0. По-

Z — Z о скольку никаких дополнительных условий не задано, то параметры ^ и 2о с Im zq > 0 можно выбрать произвольно. Например, возьмем.

= 0, 2о = г. Тогда получим w = ——-.

w. + г

4) Искомое отображение будет композицией указанных выше отображений:

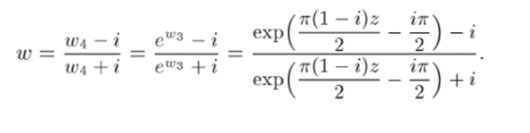
Задача 33.19. Найти все значения степени (—/3 + t) °.

Р е ш е н и е. Согласно определению общей степенной функции (см. § 12, II. 1)

Значения логарифма найдем по формуле (11.5):

где = arg (—/3 + г). Поэтому ^ лежит во второй четверти. Следовательно, <�р = 57г/6. Получаем.

Мы получили, что данная степень (— л/3 + *)^-6‘ имеет бесконечное множество значений. Все эти значения лежат на одном луче, идущем под углом 9 — — б In 2 к оси ОХ. Модули этих значений образуют две геометрические прогрессии с первым членом fci = е '^т и знаменателями q = е^У2п при к = 1,2,3,…, и </ = е~^12п при к = —1, -2, -3,…

3 ад, а ч, а 33.20. Найти все значения функции Arccos (—5/).

Р е ш е н и е. По формуле (12.3).

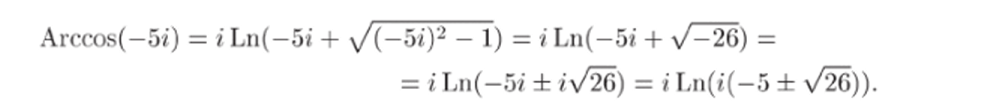
Мы пишем ± перед /26. поскольку под корнем из положительного числа обычно понимается арифметическое значение корня, в то время как иод корнем в формуле (12.3) подразумевается двузначная функция. Рассмотрим каждый из знаков перед корнем отдельно:

(мы воспользовались равенством (/26 — 5)(-/2G 4- 5) = 1). По формуле (11.5).

Можно было рассмотреть только один случай и воспользоваться общим замечанием, сделанным в § 12, согласно которому изменение знака перед корнем приво/тт к изменению знака перед логарифмом Ln(z + у/г² + 1).

— 2/3 + 3 «.

Аналогично,.

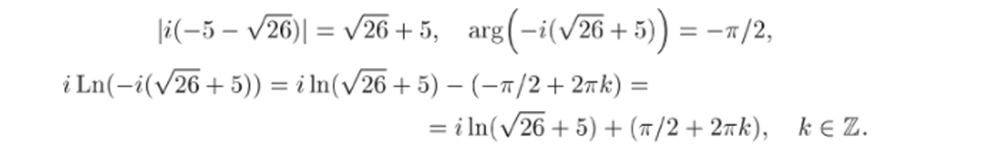
Мы пишем +2тгА: вместо —2тгЛт, поскольку к пробегает все множество целых чисел. Окончательно получаем.

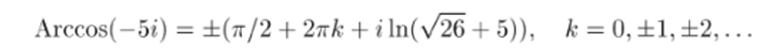
Задача 33.21. Найти все значения функции Arctg.

Г е ш е н и е. По формуле из (12.4) при z = (—2/3 + Зг)/3 имеем.

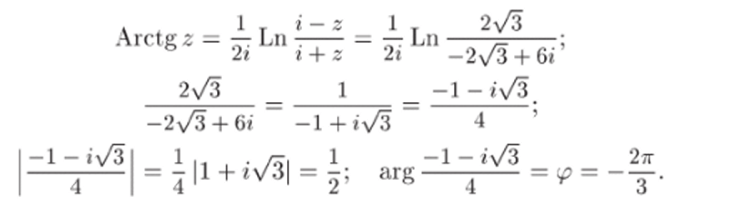
Равенство для (р следует из того, что sin<^= —д/3/2, cos.

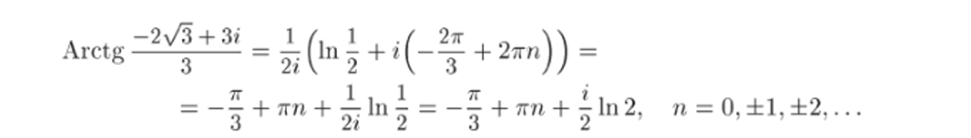
5. Задачи к главе V. Интегрирование функций комплексного переменного.

Задача 33.22. Вычислить интеграл от функции f (z) = z² по кривой Г, являющейся ломаной ЛВС, где А (—1,0), В (0,1), (7(1,0).

Р е ui е н и е. 1) Зададим кривую уравнением вида.

Поскольку кривая состоит из двух участков — отрезков ЛВ и ВС, задаваемых разными уравнениями, то рассмотрим каждый из них отдельно.

Участок АВ можно задать уравнением у = х + 1, —1 ^ а: ^ О или, в параметрической форме, x (t) = t, y (t) = t + 1, т. е. z (t) = t + i (t + 1),.

Участок ВС задается уравнением у = — х + 1, 0 ^ х ^ 1. Параметрическими уравнениями отрезка ВС являются x (t) = t, y (t) = — t + 1, или z (t) = t + i (—t. + 1), 0 ^ t ^ 1.

2) Найдем интеграл по кривой Г по формуле Для этого перейдем к сумме интегралов по участкам АВ и ВС и вычислим каждый из них в отдельности.

Для участка Л В

Задача 33.23. Проверить, является ли функция f (z) = zsin5z аналитической в С, и в случае положительного ответа найти первообразную F (z) этой функции в С, удовлетворяющую условию F (тг/2) = 0.

Решение. Проверку аналитичности функции f (z) можно сделать двумя способами. Первый способ состоит в том, что f (z) представляется в виде f (z) = и (х, у) + iv (x, y), т. е. выделяются действительная и мнимая части функции f (z). После этого вычисляются частные производные функций и (х.у) и v (x, y) и показывается, что условия Коши Римана (6.4) выполняются для любых х и у. Второй способ (более простой) основан на использовании свойств аналитических функций (§ 6).

Функция сг является аналитической в С (это доказано в § 11); функции 5iz и —5iz, очевидно, тоже аналитические. Поэтому и сложные функции e^t5z и еГ'^Ьг аналитичны в С. Отсюда следует, что и функция

будет аналитической в С как разность и произведение аналитических функций. Теперь заметим, что нужная первообразная F (z) дается формулой

где интеграл берется по любому пути, идущему от 7г/2 к г. Действительно, согласно теореме 17.1, функция F (z) будет первообразной; равенство F (tt/2) = 0 очевидно. Интеграг вычисляется по формуле Ньютона-Лейбница (17.4). При этом, как отмечаюсь в § 17, можно пользоваться обычными приемами и формулами интегрирования. В данном случае воспользуемся формулой интегрирования по частям:

В нашем случае и = С, du = d (, dv = sin5CdC> ^v = — rCos5C. Отсюда О.

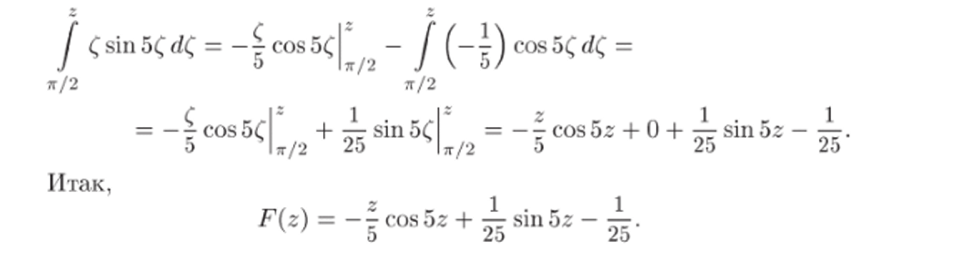
Задача 33.24. Используя теорему Коши или формулы Коши «[ cos2z ,.

для производных, наити интеграл / ^ az по замкнутому кон;

г туру Г: |z + *ir| = 2 (обход контура против часовой стрелки).

Рис. 64.

Решение. Уравнение z² + тг² = 0 имеет решения 2 = ±in. Поэтому подынтегральная функция имеет две особые точки ±in, причем точка —in лежит внутри контура Г окружности с центром —in и радиусом 2, а точка in лежит вне Г (рис. G4). Разложим знаменатель z² + тг² на множители: z² + тг² =.

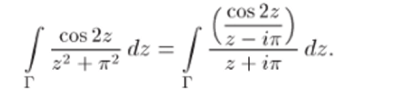
= (z + in)(z — in) и представим интеграл в виде.

. _ч cos 22.

Функция flz) =-— является аналитичес;

z — гп

кой в замкнутом круге, ограниченном контуром Г. Поэтому применима формула (18.1), в которой 2 = -in, а переменное? обозначено через z:

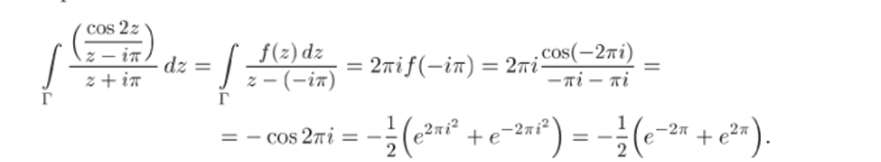
Задача 33.25. Используя теорему Коши или формулы Коши.

/_г⁵ _ 2г^л + 3.

—- dz по замкнутому г.

контуру Г: z = 5 (обход контура против часовой стрелки).

Р е ш е н и е. Обозначим f (z) = z^h — 2z⁴ + 3. Функция f (z) аналогична в замкнутом круге z ^ 5 (она аналогична даже во всей комплексной плоскости С). Точка лежит z = i внутри этого круга. Поэтому применима формула Коши дтя производных (18.4), в которой z = г, п = 3:

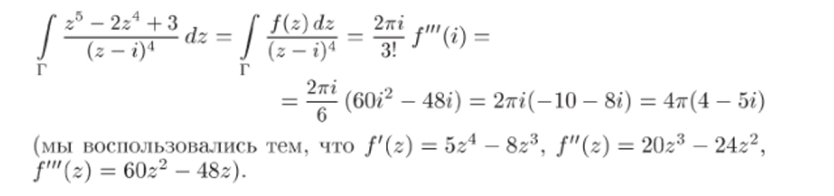
6. Задачи к главе VI. Ряды.

Задача 33.2G. Найти разложение функции.

в ряд Тейлора в окрестности точки zq = 0 и указать круг сходимости полученного ряда.

Решение. 1) Найдем вначале разложение функции.

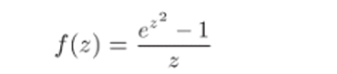
в ряд Тейлора в окрестности точки го = 0. Для этого воспользуемся известным разложением функции (формула (22.11)):

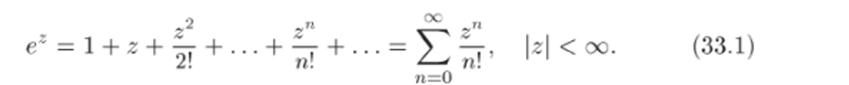
Подставляя z² вместо г и вычитая 1, имеем.

Полученный ряд. как и исходный, будет сходиться при всех z Е С. Разделим обе части равенства на г:

Этот ряд сходится при всех г Е С (включая точку го = 0) и, следовательно, определяет анатнтичсскую в С функцию. Согласно свойству 21.8, его можно почленно дифференцировать.

2) Продифференцируем обе части равенства (33.2) по переменному г:

В силу свойства 21.8 полученный ряд имеет тот же круг сходимости, что и ряд (33.2), т. е. г < оо.

Задача 33.27. Разложить функцию.

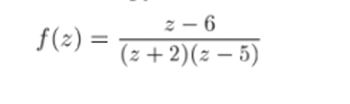
в ряд Тейлора в окрестности точки zq — 3 и указать круг сходимости полученного ряда.

Решение. 1) Сделаем замену переменного: w = z — zq = z — 3, откуда z = w + 3. Тогда.

2) Разложим полученную дробь в сумму простейших дробей:

Следовательно, w — 3 = A (w — 2) + B (w 4- 5).

При w = 2 имеем 2 — 3 = В{2 4- 5), т. е. В = —1/7.

При w = — 5 имеем -5 — 3 = А(—5 — 2), т. е. Л = 8/7.

Таким образом,.

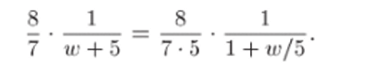
3) Каждую из полученных дробей разложим в ряд по степеням переменного? с, используя равенство (22.14):

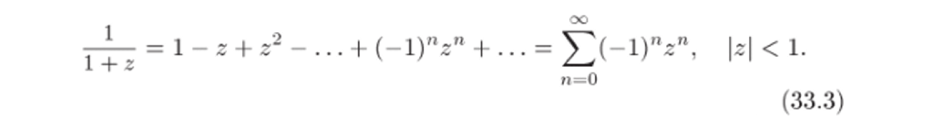
Чтобы воспользоваться этой формулой, преобразуем дробь 1 /(w 4- 5), вынеся в знаменателе за скобки множитель 5:

Подставляя в (33.3) wt5 вместо 2, получим.

Так как ряд (33.3) сходится при z < 1, то полученный ряд будет сходиться при |ic/5| < 1, т. е. при |ге| < 5.

Аналогично раскладываем дробь l/(tv — 2). Для этого выносим за скобки —2:

и подставляем в (33.3) —tv/2 вместо z:

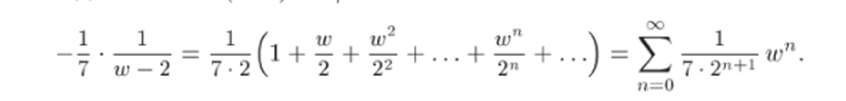
Здесь кругом сходимости будет w/2 < 1, т. е. |ш| < 2.

Складывая полученные разложения, имеем.

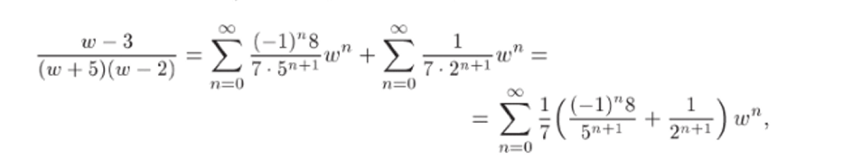
причем ряд сходится в наименьшем из кругов |ш| < 5 и |и;| < 2, т. е. в круге |и;| <2.

4) Возвращаясь к переменному г, подставляем w = z — 3 и получаем искомое разложение:

Заметим, что круг сходимости ряда Тейлора можно было найти сразу, пользуясь тем фактом, что радиус сходимости R равен расстоянию от Zq до ближайшей к zq особой точки функции f (z). В нашем случае f (z) имеет две особые точки z = -2 и 22 = 5: ближайшей к zo = 3 является Z2, и R = 5 — 3 = 2.

Задача 33.28. Найти все лорановские разложения функции по степеням (z — 3).

Решение. 1) Сделаем замену переменного: w = z — 3, т. е. z = = w + 3. Тогда

2) Разложим полученную дробь в сумму простейших дробей:

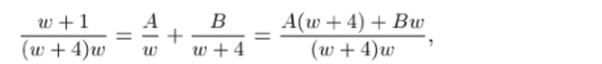
откуда w + 1 = A (w + 4) 4- Bw.

При w = 0 имеем 1 = 4А, т. е. А = ¼.

При го = —4 имеем —3 = —^413, т. е. В = ¾.

Таким образом,.

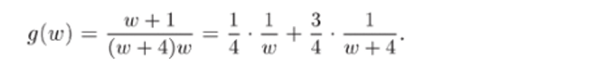
• 3) Функция g (w) имеет особые точки w = 0 и w = —4. Следовательно, она аналитична в кольцах V = {0 < |'ш| < 4} и V-2 = {4 < |tc| < < оо}. Найдем лорановские разложения в каждом из этих колец. Для
• (мы подставили в (33.3) w/4 вместо г). Так как ряд (33.3) сходится при г < 1, то полученный ряд сходится при |ш| < 4. Итак, для w 6

этого надо разложить дробь 1/(ш + 4) в ряд по степеням переменного w, пользуясь формулой (33.3).

В случае 0 < |ш| < 4 выносим за скобки в знаменателе множитель 4:

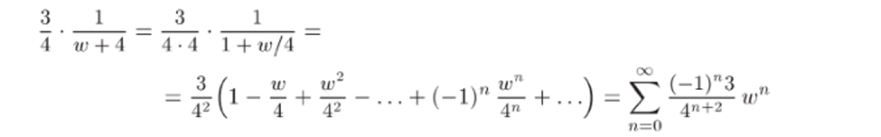
При |ic| > 4 полученный ряд расходится. Поэтому для разложения функции g (w) в кольце Vj вынесем за скобки в знаменателе дроби l/(w + 4) множитель w: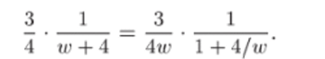

Если w >4, то 4/w < 1. Поэтому можно подставить в (33.3) 4/ш вместо z:

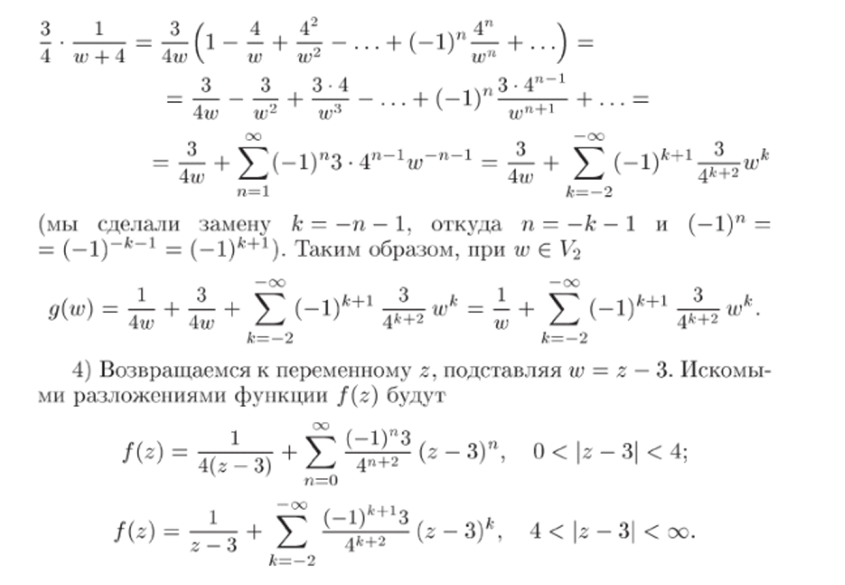
Если требуется найти лорановское разложение лишь и проколотой окрестности особой точки (например, точки zn = 3), то указанные выше действия выполняются лишь для одного из колец (в данном случае для кольца 1Т).

7. Задачи к главе VII. Изолированные особые точки и теория вычетов.

Задача 33.29. Найти разложение функции.

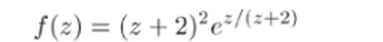
в ряд Лорана в окрестности точки го = -2. Указать кольцо сходимости, правильную и главную части разложения, а также тип особой ТОЧКИ Zq.

Р е ш е и и е. 1) Сделаем замену переменного w = z + 2. Тогда z = = w — 2,.

2) Воспользуемся известным разложением функции е~ — формулой (33.1), в которую подставим —2/w вместо z:

(в последнем равенстве мы сделали замену к = п — 2, т. е. п = к + 2).

Так как ряд (33.1) сходится при z < оо, то полученный ряд сходится при | - 2/ic| < оо, т. е. ги > 0, или w ф 0.

3) Возвращаемся к переменному г, подставляя w = z + 2. Получаем искомое разложение функции f (z):

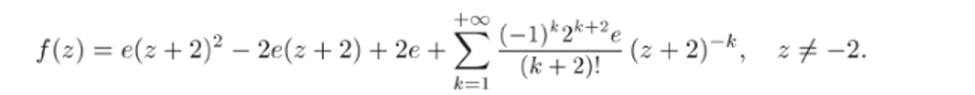
Правильной частью является сумма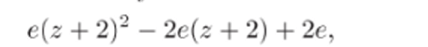

главной частью — ряд.

Поскольку главная часть имеет бесконечно много отличных от нуля коэффициентов, то zq = —2 является существенно особой точкой.

Задача 33.30. Определить тип особой точки го = 0 функции.

Р с ш с н и е. Разложим числитель и знаменатель в ряд Тейлора по степеням г. Для этого используем известное разложение функции cosz (формула (22.13)):

причем ряды сходятся во всей комплексной плоскости.

Для разложения знаменателя е~ — 1 — г³ воспользуемся формулой (33.1), в которую подставим г³ вместо г и вычтем 1 + г³:

Функция h (z) имеет вид h (z) = fi (z)//₂(г), где функции f (z) и /₂(г) аналогичны в комплексной плоскости С и /₂(0) = ½⁰. Поэтому функция h (z) также аналогична в некоторой окрестности точки zo = = 0, причем h (0) = 1⁰. Так как f (z) = h (z)/z' то, согласно следствию 26.4, точка го = 0 является полюсом порядка N = 4.

3 а д, а ч, а 33.31. Найти все изолированные особые точки функции и определить их тип.

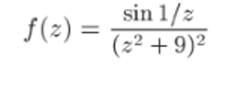
Р е ш е н и е. Конечными особыми точками являются г = 0, а также точки, в которых г² + 9 = 0, т. е. z2 = 3г и гз = -3г. Поэтому особая точка Z4 = оо тоже является изолированной, так как найдется окрестность |г| > /?, не содержащая других особых точек.

Рассмотрим точку z — 0. Пусть точки z'_n таковы, что = пп. т. е.

z'_n = —, п = 1,2,… Тогда f (z'_n) = 0. Через z" обозначим точки, для которых — = 5 + 2тгп, т. е. z" =--—. В этих точках sin — = 1,.

Zn 2 «7Г + 47ГП ^.

п = 1,2,… Легко видеть, что z_x -э 0 и 0 при п -> оо. В го же время пределы.

различны. Следовательно, функция /(г) не имеет предела при z —> 0. Поэтому точка 2i = 0 является существенно особой.

Для рассмотрения точек г-2 и гз разложим знаменатель на множители. Так как

то Поскольку функция h (z) аналитична в окрестности точки zo = Зг и.

то в силу следствия 26.4 точка z-i = 3i является полюсом второго порядка. Аналогично доказывается, что = — Зг тоже полюс второго порядка.

Осталось рассмотреть точку 24 = ос. Это можно сделать двумя способами: либо перейти к переменному w = /z и исследовать особую точку wo = 0 функции G (w) = f (l/w) (см. пример 2G.11), либо непосредственно вычислить предел lim /(г) (или доказать, что этот г—юо предел нс существует). В данном случае указанный предел легко вычисляется, поэтому второй способ проще. Действительно, 1/z —" 0 при z —? оо. Поэтому и sin (l/z) —"? 0 при z -> оо. Очевидно, что (z² + 9)² —> -" оо при z —> ос. Следовательно,.

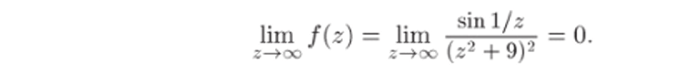
Так как функция f (z) имеет конечный предел при z —? оо, то z = = оо — устранимая особая точка (здесь несущественно, что предел равен нулю; важно, что он является конечным числом). Если положить /(оо) = 0, то f (z) станет аналитической в точке z = оо.

Задача 33.32. Вычислить интеграл.

Решение. 1) Изобразим контур интегрирования Г = {z — г| = = 2} на комплексной плоскости. Он является окружностью с центром zq = i и радиусом 2 (рис. 65).

2) Найдем все особые точки функции, попавшие внутрь контура, и исследуем их характер. Функция

имеет три особые точки: Z = —1, = 2i и.

Z3 = —2i. Из них Z и z-2 лежат внутри кон- ‘ ^ис' ^.

тура, a Z3 — вне его (см. рис. 65). Из следствия 26.4 легко получаем, что Z является полюсом второго порядка, a z2 — полюсом первого порядка.

3) В каждой из особых точек внутри контура найдем вычет функции f{z). Вычет в тючке Z2 = 2г найдем, но формуле (27.5):

Для вычисления вычета в точке -1 применим формулу (27.7) с п = 2:

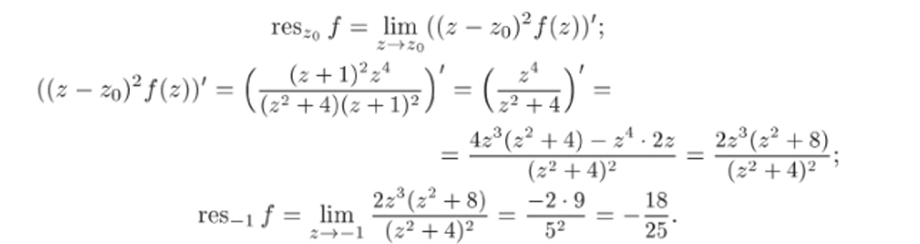
4) Используя основную теорему о вычетах (теорема 27.1), найдем искомый интеграл по формуле.

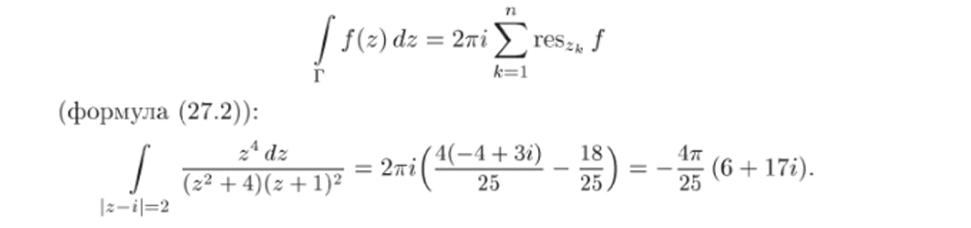
Задача 33.33. Вычислить вычет функции f (z) = (z + 2) е ¹^^г в бесконечно удаленной точке.

Решен и е. 1) Проверим, является ли особая точка zq = эо изолированной. Для этого установим, существует ли окрестность точки 2о = оо — внешность какой-либо окружности z = R, — в которой пет других особых точек, кроме Zo = эо. Функция f (z) = (z + 2)e~^l/^z имеет единственную конечную особую точку z = 0. Поэтому во внешности любой окружности z = R (например, в z > 1) нет особых точек, кроме zq = ос.

2) Искомый вычет reSoc/ найдем двумя способами.

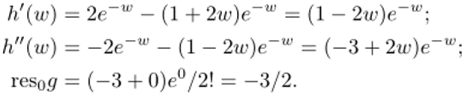
Согласно формуле (27.13), res^o/ = — reso# = 3/2.

1-й способ — по формуле (27.13). Здесь.

где h (w) = (1 + 2w)e~^w. Поскольку функция h (w) аналитична в окрестности точки Wq = 0 и /г (0) ^ 0, то согласно следствию 26.4 wo — полюс 3-го порядка. Вычет resoд найдем по формуле resog = h" (0)/2! (формула (27.7') с п = 3):

2-й способ — но формуле (27.9). Для нахождения коэффициента с_ 1 сделаем замену переменного w = 1/z и подставим z = 1/w в f (z):

Найдем коэффициент при w¹ в лорановском разложении функции G (w) по степеням переменной w. Этот коэффициент будет коэффициентом С-1 при z~^l в разложении Лорана функции f (z) по степеням z. Чтобы найти нужное разложение функции G (w), воспользуемся формулой (33.1). Подставляя в эту формулу (—w) вместо получаем:

(оставшиеся слагаемые содержат степени w не ниже второй). Коэффициент при w^l равен с~ = —3/2.

В силу формулы (27.9), res= — c_i = 3/2. Как видим, оба способа дают один и тот же результат.

aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">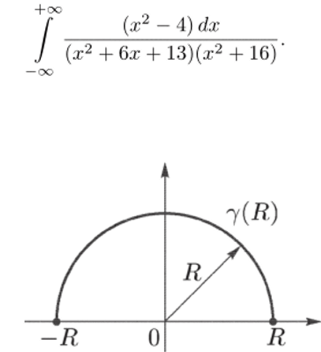

Рис. 66.

Р е ш е н и е. Как и в теореме 28.4, рассмотрим замкнутый контур, состоящий из отрезка [—Я, Я] действительной оси и полуокружности 7(Я) радиуса Я, лежащей в верхней полуплоскости (рис. 66). Возьмем функцию

которая получается, если неременное х в подинтегральном выражении заменить на z. Покажем, что.

(т.е. что выполнено условие (28.3) теоремы 28.4). Действительно,.

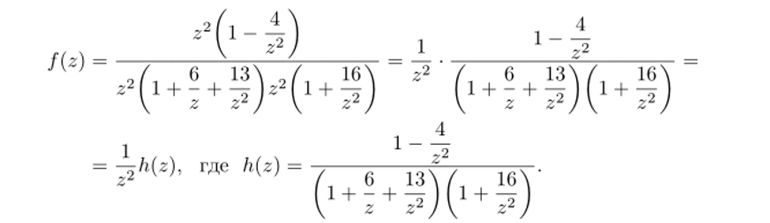
Так как h (z) —> 1 при 2 —> ос, то для достаточно больших значений 2 будет h (z) < 2. Поэтому f (z) = |М-^г:)|/И² < 2/z². Следовательно, при достаточно больших R

Переходя к пределу при R —> оо, получаем (33.5). (Заметим, что мы уже проводили аналогичные рассуждения в примере 28.5).

В силу теоремы 28.4 интеграл f_™ f (x) dx равен сумме вычетов функции f (z) в особых точках, лежащих в верхней полуплоскости, умноженной на 2iri. В нашем случае особыми будут точки, в которых знаменатель обращается в нуль, т. е. z² + Qz + 13 = 0, откуда z^ = —3 ± 2 г, и z² + 16 = 0, откуда 23,4 = ±4г. Из этих точек в верхней полуплоскости лежат только z = — 3 + 2 г и z$ = 4 г. Так как.

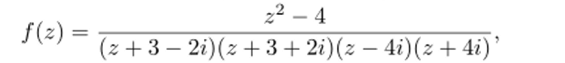aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">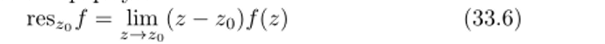

(формула (27.5)). Для сравнения найдем res₃+2, / двумя способами. Вначале применим (27.6'). Представим f (z) в виде то в силу следствия 26.4 каждая особая точка является полюсом первого порядка. Вычеты в точках z и 23 удобно найти либо по формуле (27.6'), либо, но формуле.

Заметим, что вычислительная часть в этих подходах, по существу, одна и та же. Рекомендуем читателю применять какую-либо одну из этих формул.

Вычет res.uf найдем, но формуле (33.6):

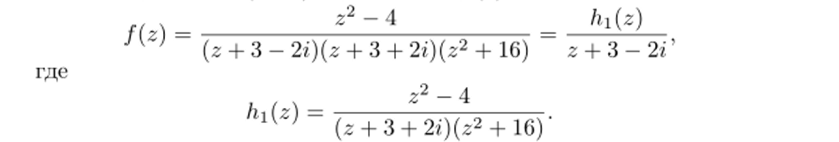
Поскольку функция h (z) аналитична в точке zq = —3 + 2 г и h (z) ^ О, то в силу (27.6') имеем:

Из этих точек только Z лежит внутри окружности z = 1, поскольку 1−221 = 7/х/21 > 1. Так как функция f (z) представима в виде.

то обе особые точки z и z^ — полюсы первого порядка. Найдем теперь вычет в точке z по формуле (33.6):

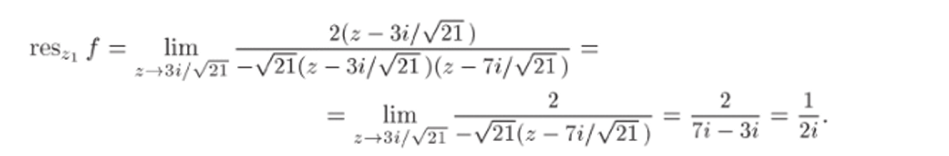
Используя основную теорему о вычетах, получаем.

Таким образом, исходный интеграл равен тг.

8. Задачи к главе VIII. Основы операционного исчисления.

Задача 33.36. По данному на рис. 67 графику оригинала f (t) найти изображение.

Решение. 1) Найдем изображение более простых оригиналов, из которых затем составим заданный оригинал f (t). Обозначим.

Изображение функции /2(f) найдем непосредственно по формуле.

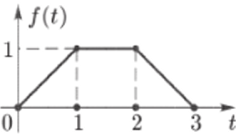
Рис. 67.

определяющей преобразование Лапласа. Если.

Изображение Fi (p) тоже можно найти по формуле (33.7), интегрируя, но частям. Но можно поступить иначе: заметить, что f (t) = ?/2(2), и воспользоваться теоремой о дифференцировании изображения 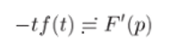(формула 23 таблицы), согласно которой.

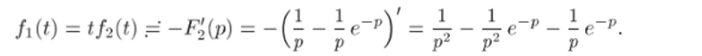
Итак,.

2) Выразим заданный оригинал f (t) через fi (t) и hW- Очевидно, что f (t) = fi (t) при 0 s$ * i? 1. На участке [1,2| f (t) совпадает с /2(2), сдвинутой на 1 вправо, т. е. J (t) = />(f — 1), 1 ^ t ^ 2. При 2 ^ t ^ 3 функцию f (t) можно получить, если сдвинуть f (t) на 2 единицы вправо, отразить симметрично относительно оси t (т.е. умножить на — 1) и поднять на 1 вверх. Таким образом. f (t) = —f (t — 2) + f>(t — 2), 2 ^ t ^ 3. Итак,

3) Пользуясь линейностью преобразования Лапласа и теоремой запаздывания (формула 18 таблицы), получаем.

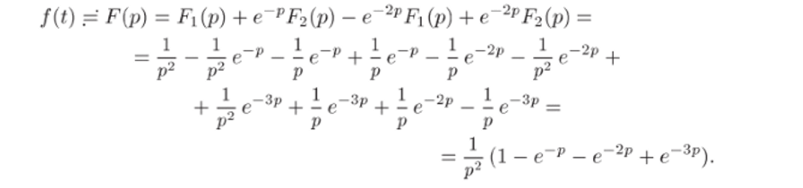
К этому же результату можно прийти, непосредственно применяя формулу (33.7). Для этого следует задать функцию f (t) аналитически и проинтегрировать на каждом из трех участков в отдельности. Такой путь приводит к существенно более громоздким вычислениям.

Задача 33.37. Найти оригинал изображения.

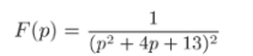
и сделать проверку, найдя изображение полученного оригинала.

Решение. 1) Разложим функцию F (p) на множители, оригиналы которых известны:

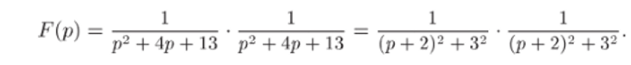
Согласно теореме умножения изображений (формула 25 таблицы), произведению изображений соответствует свертка оригиналов сомножителей. Поэтому.

Вначале мы вынесли постоянный множитель i е ²¹ за знак интеграла, а затем воспользовались формулой.

sin a sin/? = ^ (cos (a — /?) — cos (af ft)).

Вычисляя последний интеграл, получаем.

Пользуясь линейностью преобразования Лапласа, имеем.

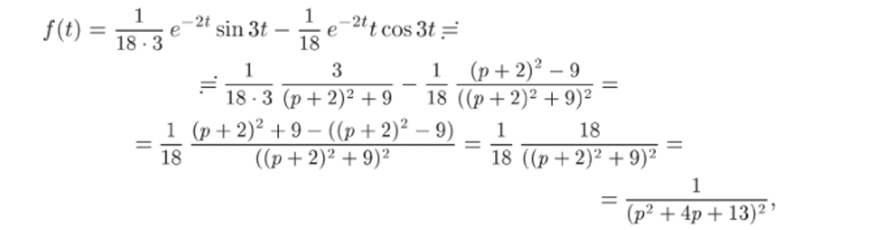
что совпадает с исходным изображением.

Задача 33.38. Двумя способами (используя метод неопределенных коэффициентов и с помощью вычетов) найти оригинал дробнорациональной функции.

Решение. А. С использованием метода неопределенных коэффициенте в.

1) Разложим дробно-рациональную функцию F{p) в сумму простейших дробей. Так как уравнение р² + Ар + 5 = 0 действительных корней нс имеет, то разложение заданной функции в сумму простейших дробей имеет вид.

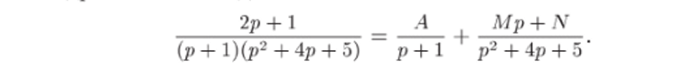
(Можно было разложить квадратный трехчлен р² + 4р + 5 на множители (р — р){р — Рг) ^с комплексными pi и />2, но это менее удобно.) Приводя правую часть к общему знаменателю, равному знаменателю левой части, и приравнивая числители дробей в левой и правой частях, получим

Подставляя р = -1, имеем -1 = Л (1 -4 + 5), -1 = 2Л, Л = —½.

При р = 0 получаем 1 = 5Л + ЛГ, откуда N = 1 — 5Л = 1 + 5/2 =.

= 7/2.

Приравнивая коэффициенты при р² в левой и правой частях равенства. получаем 0 = Л + М, М = — Л = ½. Итак,.

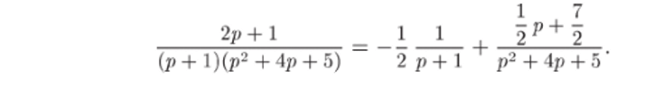
Для определения порядка полюсов функции разложим знаменатель на линейные множители:

2) Для каждой простейшей дроби найдем оригинал, используя таблицу соответствия оригиналов и изображений. Из формулы 2 таблицы с а = — 1 следует.

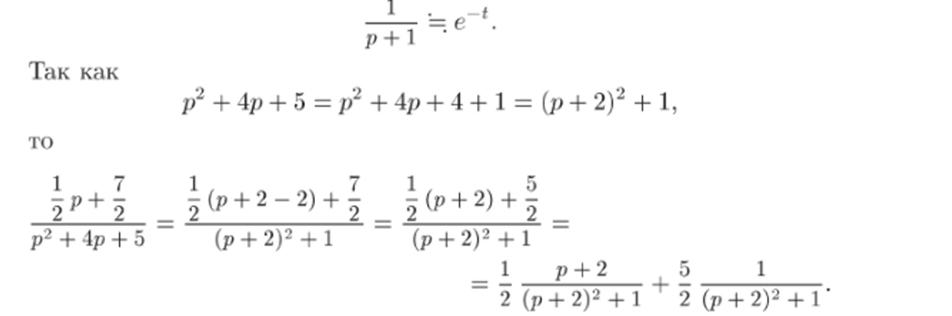
По формулам 8 и 7 таблицы с, а = — 2 и w = 1 получаем.

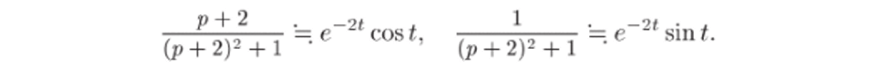
3) Используя свойство линейности преобразования Лапласа, найдем оригинал f (t) заданной функции-изображен и я F (p). Так как.

Б. С помощью вычет о в.

1) Найдем нули знаменателя дроби F (p), являющиеся полюсами этой функции. Решая уравнение /У² + 4р + 5 = О, получаем.

Отсюда следует, что функция F (p) имеет три особые точки: Каждая из них является полюсом первого порядка.

2) Найдем вычеты функции F (p)e^pt в каждом из найденных полюсов Рк по формуле (33.6) (можно воспользоваться и формулой (27.6^;)):

Найденный оригинал совпадает с тем, который был получен первым способом. Действительно,.

Задача 33.39. Найти решение дифференциального уравнения.

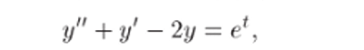
удовлетворяющее начальным условиям у (0) = — 1, </'(0) = 0.

Решение. 1) Считая неизвестную функцию у = y (t) и правую часть f (t) = е* уравнения оригиналами, перейдем от данного уравнения, связывающего оригиналы, к операторному уравнению, связывающему их изображения Y = Y (р) и F = F (p). Для этого восполь;

зуемся теоремой о дифференцировании оригинала и таблицей соответствия. По формуле 21 таблицы с п = 2 получаем.

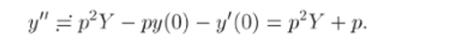
По формуле 20 имеем.

Формула 2 дает е¹ = 1 /(р — 1). Поэтому операторным уравнением, соответствующим данному, является уравнение.

2) Полученное уравнение является линейным алгебраическим уравнением первого порядка относительно неизвестного изображения У = У (р). Чтобы найти это изображение, преобразуем уравнение к виду.

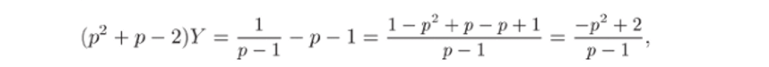
откуда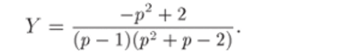

3) Перейдем от найденного изображения У (р) к оригиналу y (t). Тем самым мы и получим искомое решение дифференциального уравнения.

Уравнение р² + р — 2 = 0 имеет решения 1 и -2. Поэтому р² + р — — 2 = (р — 1)(р + 2) и.

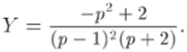
Для отыскания оригинала y (t) можно применить любой из известных методов (см. задачу 33.38). Воспользуемся, например, методом неошюделенных коэффициентов. Имеем.

При р = 1 получаем 1 = 3 В, т. е. В = 1/3; при р = —2 будет —2 = 9(7, т. е. С = —2/9. Сравнивая коэффициенты при р² в левой и правой часгях равенства, получим — 1 = А -IС, т. е. А = — 1 — С = —7/9.

Решение. Применение интеграла Дюамеля в данном случае вызвано, в частности, тем, что таблица не содержит изображения правой части уравнения. Решение состоит из следующих двух этапов.

1) Найдем решение yi (0) уравнения

с той же левой частью, что у заданного уравнения, и также при нулевых начальных условиях: у(0) = 0, */5(0) = 0. С этой целью перейдем к операторному уравнению, пользуясь тем, что по формулам 20, 21 и 1 таблицы у[ = (р), у" = р² (р), 1 = 1/р (здесь У (р) — изобра жение функции y (t)):

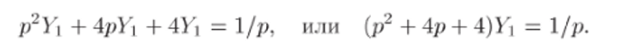aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">

Разложение полученной дроби в сумму простейших дробей имеет вид.

Пользуясь формулой 2 таблицы и формулой 10са=1,п = 1, получаем.

Задача 33.40. Используя интеграл Дюамеля, найти решение дифференциального уравнения.

удовлетворяющее начальным условиям t/(0) = 0. */'(0) = 0.

Отсюда.

Следовательно, 1 = А (р + 2)² + Вр (р + 2) + Ср.

При р = 0 имеем 1 = 4,4, т. е. А = ¼; при р = -2 будет 1 = -2С, г. е. С = —½. Сравнивая коэффициенты при р² в левой и правой частях равенства, получим 0 = А + В, т. е. В = —А = —¼. Итак,.

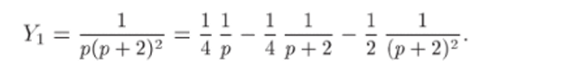
Пользуясь формулами 1, 2 и 10 таблицы с n = 1, имеем.

Заметим, что найти у можно также методом неопределенных коэффициентов, изучаемым в курсе дифференциальных уравнений.

2) Найдем решение исходного уравнения по формуле.

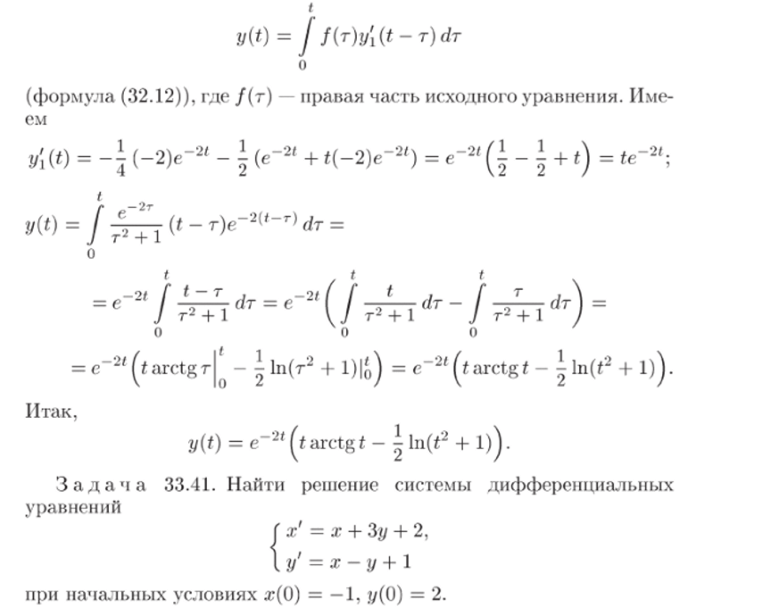
Решение. 1) Обозначим через X и У изображения неизвестных функций х = x (t) и у = y (t). Пользуясь линейностью преобразования Лапласа и формулами 20 и 1 таблицы, перейдем к операторным уравнениям.

2) Решим полученную систему линейных уравнений относительно X и Y. Для этого выразим X из второго уравнения и подставим в первое:

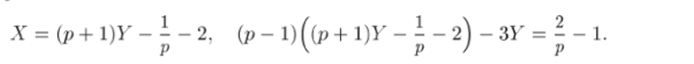
Дая сравнения решим эту систему другим способом, с использованием формул Крамера (см. также пример 32.5). Из коэффициентов при X и Y составим определитель А:

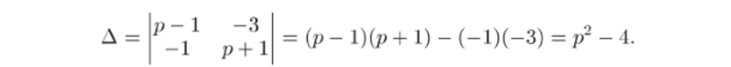
После раскрытия скобок и приведения подобных членов приходим к равенству.

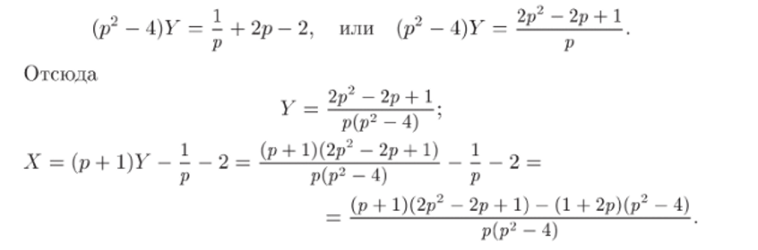
Раскрывая в числителе скобки и приводя подобные члены, получим Последовательно заменяя первый и второй столбцы этого определителя столбцом из правых частей уравнений, получим, соответственно, определители A v и Ду:

Формулы Крамера сразу приводят к тому же результату:

Читатель может убедиться, что второй способ требует несколько меньшего объема вычислений.

3) От полученных изображений X и Y перейдем к их оригиналам х и у. Сделать это можно двумя способами: методом неопределенных коэффициентов и с помощью вычетов; объем работы при использовании этих методов примерно одинаков. Чтобы еще раз напомнить оба приема, мы (как и в примере 32.5) найдем x (t) первым способом, a y (t) — вторым; читателю рекомендуется находить оба оригинала каким-либо одним способом, что более удобно.

Разложение функции X в сумму простейших дробей имеет вид.

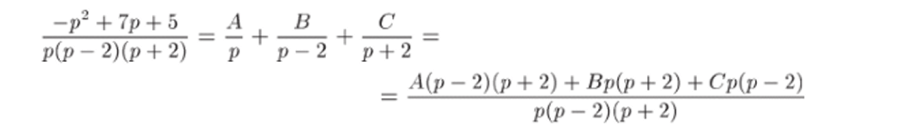
(каждый множитель знаменателя является множителем вида (ар + Ь)^к с к = 1). Отсюда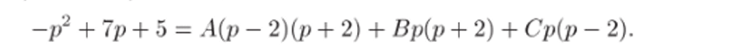

При р = 0 получаем 5 = —4.4, откуда Л = —5/4.

При р = 2 получаем —4 4- 14 + 5 = В • 2 • 4, откуда В = 15/8.

При р = — 2 получаем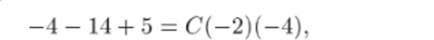

откуда С = -13/8. Следовательно,.

По формулам 1 и 2 таблицы и свойству линейности находим оригинал:

Оригинал y (t) найдем по формуле.

(формула (32.8)). Функция.

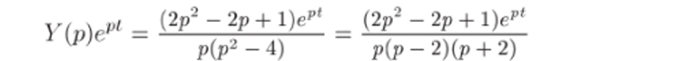
имеет особые точки 0, 2 и —2, каждая из которых является полюсом первого порядка. Вычеты в этих точках найдем по формуле.

(см. формулу (27.5); можно использовать и (27.6^/)). Имеем.