Сложность информационных графов

Из определения функционирования ИГ естественным образом вытекает, что каждому ИГ U можно сопоставить следующую процедуру поиска.

Предполагается, что эта процедура хранит в своей (внешней) памяти структуру ИГ U. Входными данными процедуры является запрос. Выходными данными является множество записей.

Пусть на вход процедуры поступил запрос х. Вводим понятие активного множества вершин и вносим в него в начальный момент корень ИГ U и помечаем его. Далее по очереди просматриваем вершины из активного множества и для каждой из них проделываем следующее:

• • если рассматриваемая вершина — лист, то запись, приписанную вершине, включаем в ответ;
• • если рассматриваемая вершина переключательная, то вычисляем на запросе х переключатель, соответствующий данной вершине, и если конец ребра, исходящего из рассматриваемой вершины, нагрузка которого равна значению переключателя, непомеченная вершина, то помечаем его и включаем в множество активных вершин;
• • если рассматриваемая вершина предикатная, то просматриваем по очереди исходящие из нее ребра и вычисляем значения предикатов, приписанных этим ребрам, на запросе х. Концы ребер, которым соответствуют предикаты со значениями, равными 1, если они непомеченные, помечаем и включаем в множество активных вершин;
• • исключаем рассматриваемую вершину из активного множества.

Процедура завершается, но исчерпании активного множества.

Заметим, что если ИГ разрешает задачу /, то множество, полученное на выходе процедуры, будет содержать все те и только те записи библиотеки (?/), которые удовлетворяют запросу х. То есть, полученная процедура решает ЗИП I = (X, V, p), где V = ((/), и, значит, является алгоритмом поиска.

Таким образом, ИГ как управляющая система может рассматриваться как модель алгоритма поиска, работающего над данными, организованными в структуру, определяемую структурой ИГ.

В данном разделе мы введем понятия сложности ИГ, которые будут характеризовать такие общепринятые меры сложности алгоритмов поиска как объем памяти, время поиска в худшем случае и время поиска в среднем.

Отметим, что в большинстве работ, посвященных исследованию сложности алгоритмов поиска, под сложностью алгоритма понимается время поиска в худшем случае [56, 70, 86, 113, 115, 116, 118, 119, 125, 126, 144, 147, 149−152, 165, 178, 179, 183, 212, 216), и в сравнительно редких случаях (см., например, [50, 56, 120, 124, 143, 184,.

186, 188, 190, 199, 210]) исследуется среднее время поиска, хотя для задач поиска, используемых в базах данных, для которых характерны массовость и многократность, исследование среднего времени поиска представляется более актуальным. Некоторое объяснение крена в сторону изучения сложности в худшем случае можно найти в цитате из [86, с. 20]: «К сожалению, анализ поведения в среднем значительно более сложная вещь, чем анализ худшего случая, по двум причинам: во-первых существенные математические трудности возникают, даже если удачно выбрано исходное распределение; во-вторых, часто с трудом достигается согласие в том, что именно выбранное распределение является реальной моделью изучаемой ситуации. Вот почему преобладающее большинство результатов связано с анализом худших случаев.».

Определим понятие сложности ИГ на запросе.

Будем считать, что время вычисления любого переключателя из G примерно одинаково и характеризуется числом а, а время вычисления любого предиката из F — числом Ь.

Пусть нам дан некий ИГ U и произвольно взятый запрос х? X.

Сложностью ИГ U на запросе х назовем число.

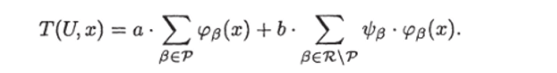
Величина T (U, x) характеризует время работы описанной выше процедуры поиска, сопоставленной ИГ U, поскольку T (U, x) равно количеству переключателей, вычисленных данной процедурой при подаче на ее вход запроса х, умноженное на а, плюс количество вычисленных предикатов, умноженное на 6.

Сложность ИГ можно вводить двумя способами. Во-первых, как максимальную сложность на запросе.

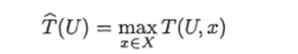
(здесь мы берем шах, а не sup, так как Т (?/, х) принимает целые значения, и, значит, sup всегда достигается). Эта величина характеризует время поиска в худшем случае соответствующим ИГ алгоритмом и ее будем называть В-сложностью ИГ (верхней сложностью). Эта величина исследуется в большинстве работ, посвященных проблемам сложности задач поиска.

Во-вторых, можно вводить сложность ИГ как среднее значение сложности ИГ на запросе, взятое по множеству всех запросов. С этой целью введем вероятностное пространство над множеством запросов X, под которым будем понимать тройку (X, сг, Р), где а — некоторая алгебра подмножеств множества X, Р — вероятностная мера на <�т, т. е. аддитивная мера, такая, что Р (Л*) = 1.

В связи с тем, что мы ввели вероятностное пространство над множеством запросов, уточним понятие типа. А именно, под типом

будем понимать тройку 5 = (Х> Y, р), считая, что множество запросов X рассматривается вместе со своим вероятностным пространством (X, <�т, Р). В тех же случаях, когда мы хотим явно выделить рассматриваемое вероятностное пространство над X, мы будем представлять тип пятеркой S = (X, У, р, <�т, Р).

Скажем, что базовое множество Т = (F, G) измеримое, если алге;

л бра а содержит все множества ЛГ/, где / G F U G.

Справедлива следующая лемма.

Лемма 1. Если базовое множество Т = (F, G) измеримое, то для любого ИГ U над базовым множеством Т функция T (U, x), как функция от х, является случайной величиной.

Доказательство. Нам необходимо доказать, что для любого ИГ U над базовым множеством Т и любого действительного числа г множество {хбХ: T (U, х) < г} € <7.

Покажем, что (р G И (У)) —> G <�т).

Пусть р G 7l (U). Пусть Ср — множество всех ориентированных цепей ИГ U, ведущих из корня в вершину р. Пусть С — некоторая цепь, а с — некоторое ребро. Через в (с) обозначим проводимость ребра с.

Нетрудно видеть, что.

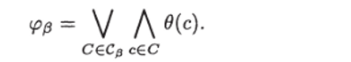aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">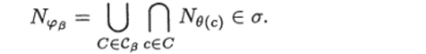

Учитывая, что N/vp = Nf U N_g, Nf^_g = Nf П N_g, имеем Введем следующее обозначение:

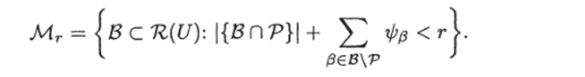
Тогда, как нетрудно видеть,.

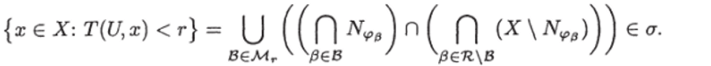
Тем самым лемма доказана.

Далее всюду будем предполагать, что базовое множество измеримо.

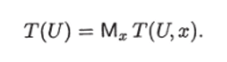
Сложностью ИГ U назовем математическое ожидание величины Т (С/, я), т. е. число Если (/?, а) — ребро ИГ, то сложностью этого ребра назовем число • Ь • Р— если (/?, а) — предикатное ребро;

• а • P (N_Vfi)/il>p — если это ребро переключательное.

Если 0 — вершина ИГ, то число Р (Л^) назовем сложностью вершины 0.

Нетрудно показать, что сложность ИГ равна сумме сложностей ребер ИГ. В самом деле.

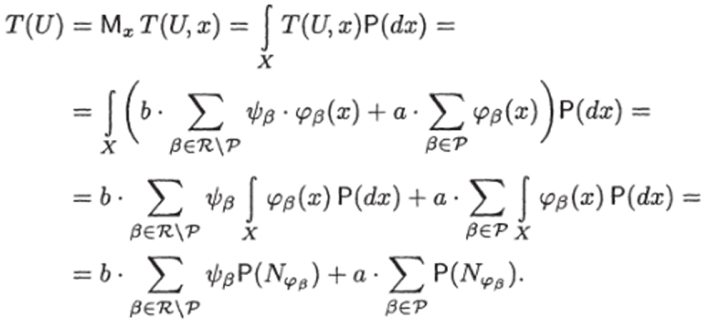
Далее всюду будем предполагать, что а = b = 1.

Пусть нам дан ИГ U.

Объемом Q (U) ИГ U назовем число ребер в ИГ U.

В качестве примера мы можем подсчитать сложность ИГ (/, изображенного на рис. 1.5. Легко видеть, что Q (U) = к и T (U) = fc, т. е. объем графа минимально возможный, а время максимальное. Это и не удивительно, так как ИГ U соответствует переборному алгоритму поиска.

Пусть нам дана некая ЗИП Юложпостью задачи I при базовом множестве Т и заданном объеме q назовем число.

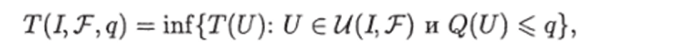
где U (l, Т) — множество всех ИГ над базовым множеством Т, разрешающих ЗИП /.

Соответственно В-сложностью задачи I при базовом множестве Т и заданном объеме q назовем число.

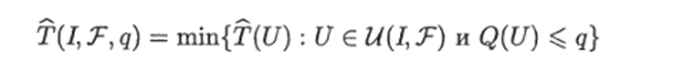
/ч.

(здесь мы берем min, а не inf, так как T (U) принимает целые значения, и, значит, inf всегда достигается).

Число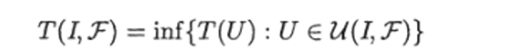

назовем сложностью задачи I при базовом множестве Т.

Соответственно В-сложностью задачи I при базовом множестве Т назовем число.

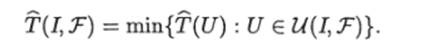
Если к — натуральное число, 5 — тип задач поиска, то обозначим.

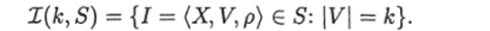
Будем исследовать функции, характеризующие сложность класса ЗИП Z (fc, 5), такие как функции Шеннона:

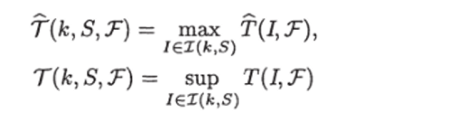
(в первом случае мы берем max, а не sup, так как Т (1,Т) принимает целые значения, и, значит, sup всегда достигается) и как средние значения: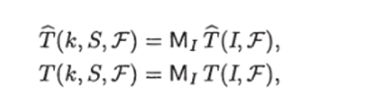

где среднее значение берется по всем ЗИП I G Z (fc, S).

Если существует такой ИГ U € U (I, Т), что T (U) = T (/, Z*), то ИГ U будем называть оптимальным для ЗИП I. Соответственно.

/ч ^*4.

если T (U) = Т (/, Т), то ИГ U будем называть В-оптималъным для ЗИП I.

Можно привести пример такой ЗИП и такого базового множества, для которых не существует оптимального ИГ.

Пусть X = Y = [0,1] и на X задана равномерная вероятностная мера. Пусть отношение поиска есть отношение для действительных чисел. Пусть библиотека состоит из одной записи V = {¾}. Пусть базовое множество имеет вид Т = {/% 0), где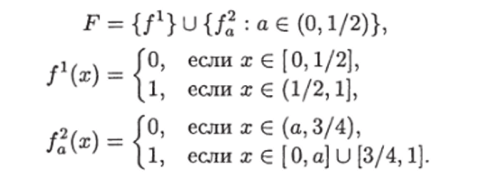

Рассмотрим ЗИП I = (X, V, ^). Поскольку.

то Хз/4,> = Гдля любого а 6 (0,½). Рассмотрим ИГ (7_а, состоящий из двух последовательно соединенных ребер, начало первого из которых есть корень ИГ, а конец второго — лист, которому приписана запись первому ребру соответствует предикат /^, а второму — f

Нетрудно видеть, что T (U_a) = 1 4- а 4- ¼ = 5/4 -На. Очевидно, что Т (1,Т) = inf{T (U_Q): а? (0,½)} = 5/4, но не существует ИГ, чья сложность равна 5/4.

Скажем, что некая вершина ИГ достижима из корня на запросе х € X или просто достижимая па запросе х € X, если функция фильтра этой вершины на запросе х равна 1.

Скажем, что некая вершина ИГ достижима из корня или просто достижимая, если функция фильтра этой вершины не равна тождественному нулю, в противном случае вершину называем недостижимой. Скажем, что ребро ИГ несущественное, если выполняется хотя бы одно из следующих условий.

• • ребро исходит из недостижимой вершины,
• • ребро является предикатным и входит в корень или в недостижимую вершину,
• • ребро является предикатным и не принадлежит ни одной цепи, ведущей из корня в какой либо лист,
• • ребро является переключательным, и начало этого ребра не принадлежит ни одной цепи, ведущей из корня в какой либо лист,
• • ребро является переключательным, и число, приписанное этому ребру, больше максимально возможного значения переключателя, соответствующего началу этого ребра,
• • начало и конец ребра совпадают.

В противном случае ребро называем существенным.

Легко заметить, что удаление несущественных ребер из ИГ не изменяет функционирования ИГ и не увеличивает его сложность. Поэтому всегда в дальнейшем мы будем рассматривать ИГ с точностью до несущественных ребер, а точнее будем считать, что все ребра в ИГ — существенные.

Теорема 3 (о существовании оптимальных графов). Если множество запросов X конечно, то для любой ЗИП I = (X, Y, p) и любого базового множества Т = (F, G) такого, что U{I, F) ф 0, существует оптимальный ИГ над базовым множеством Т.

Доказательство. Заметим, что из-за конечности множества X множества F и G конечны. В самом деле, если |Х| = т, то число предикатов, определенных на X не больше, чем 2^т. Следовательно, |F| ^ 2^т. Так как область значений любого переключателя есть начальный отрезок натурального ряда, то любой переключатель над X принимает не более т значений, следовательно |(2| < т^т.

Для произвольного ИГ U обозначим через N (U) подграф графа U, состоящий из ребер, имеющих ненулевую сложность.

Возьмем произвольный ИГ Uq € ?V (/, Т). Обозначим W = {U € € T (U) ^ T (C/₀)h М' = {АГ (Г/): U в U'}. Очевидно, что.

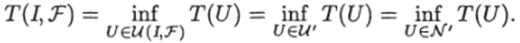
Для доказательства существования оптимального ИГ для ЗИП / нам достаточно показать конечность множества ЛЛ Пусть |F U G — п. Пусть М — множество, состоящее из тождественно нулевого предиката и всех предикатов, полученных из предикатов множества F U G с помощью операций конъюнкции и дизъюнкции. Понятно, что М ^ min (2^m, 2²). Обозначим М' = {/ 6 М: Р(N/) >0}. Пусть min Р(N/) = г. По определению г > 0. Поскольку для любого ИГ над Т функции фильтров вершин принадлежат множеству М, то сложность любого предикатного ребра ИГ над Т либо нулевая, либо не меньше чем г, а сложность любого переключательного ребра с ненулевой сложностью не меньше чем r/m. Отсюда в любом ИГ из множества ЛЛ число ребер не больше чем T (Uq) • т/г.

Так как из конечности множеств F и G следует конечность числа различных нагрузок ИГ, то, значит, множество Л/⁷ конечно.

Что и доказывает теорему.

Упражнения

• 1.17. Пусть X = {1,2,…, N}_y 5 = (X, X, =, Р, а) — тип поиска идентичных объектов, где о — 2^х, Р — равномерная вероятностная мера, т. е. для любого х € X выполняется Р (х) = 1/N.
• 1. Посчитайте сложность, В-сложность и объем информационного графа, полученного при решении упражнения 1.6.
• 2. Посчитайте сложность, В-сложность и объем информационного графа, полученного при решении упражнения 1.7.
• 3. Посчитайте сложность, В-сложность и объем информационного графа, полученного при решении упражнения 1.8. Для базового множества и ЗИП, приведенных в упражнении 1.8, постройте информационный граф со сложностью, не большей, чем 1.48.
• 4. Посчитайте сложность, В-сложность и объем информационного графа, полученного при решении упражнения 1.9, если N = 100. Для какого значения параметра m сложность будет минимальна. Для какого значения параметра m В-сложность будет минимальна. Для какого значения параметра m объем будет минимальным.
• 1.18. Если X = {1,2,…, 7V} инаХ задана равномерная вероятностная мера, то посчитайте сложность, В-сложность и объем информационного графа, полученного при решении упражнения 1.10.
• 1.19. Пусть на множестве запросов X = [0,1] задана равномерная вероятностная мера. Посчитайте сложность, В-сложность и объем информационного графа, полученного при решении упражнения 1.11.
• 1.20. Пусть на множестве запросов X"_n* = {(u, v): 0 ^ и ^ v ^ 1} задана равномерная вероятностная мера. Посчитайте сложность, В-сложность и объем информационного графа, изображенного на рис. 1.1.