Расчет рам на действие температуры

Канонические уравнения при расчете рамных систем на действие температуры запишутся в виде.

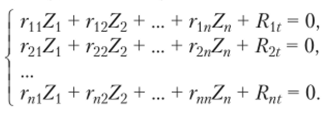
Коэффициенты при неизвестных ц, ij =1,2,…, п, определяются так же, как и при действии нагрузки. Для определения реакций в связях основной системы от действия температуры необходимо вначале изучить состояние отдельного стержня с разными закреплениями его концов при неравномерном нагреве. На рис. 9.18, а показан стержень с двумя заделками, которые препятствуют повороту концевых сечений, но позволяют им свободно перемещаться вдоль оси стержня. Температура линейно изменяется по высоте сечения h от t до t₂> но по длине стержня остается постоянной.

Представим такое воздействие в виде двух состояний, показанных на рис. 9.18, бив.

В первом состоянии с обеих сторон стержня действует одинаковая температура, равная средней температуре t_cp = = (?_t + t₂)/2. В этом случае происходит равномерный нагрев всех волокон, ось стержня остается прямой, а длина стержня увеличивается на Д/ = at_cpl.

Во втором состоянии кососимметричного действия температуры длина стержня остается неизменной, а его ось искривляется. Величина At равна разности температур, At = t — t₂.

Если два указанных состояния сложить, получим заданное состояние, изображенное на рис. 9.18, а. В самом деле, температура нижнего волокна будет t_cp + At/2 = t_b а температура верхнего волокна будет ?_ср — At/2 = t₂.

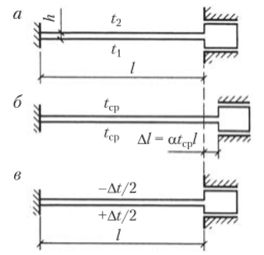
Изгибающие моменты в стержне, изображенном на рис. 9.18, а, будут такими же, как в стержне, показанном на рис. 9.18, в. Для определения этих моментов применим метод сил, для этого выберем основную систему в виде простой балки, а влияние заделок компенсируем моментами X (рис. 9.19, в).

Задача легко решается путем сравнения деформаций от темпера;

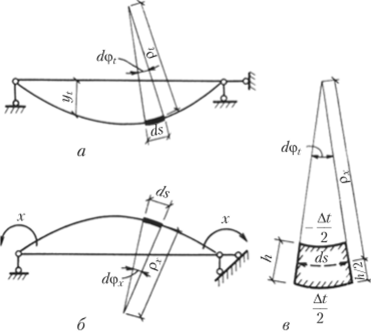
Рис. 9.19.

туры (рис. 9.19, а) и от концевых моментов X. Из рис. 9.19, б, где показан элемент балки ds, искривившейся от действия температуры, очевидно, что.

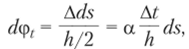
или.

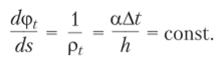
Таким образом, от действия неравномерного нагрева ось стержня искривляется по окружности. С другой стороны, при чистом изгибе, показанном на рис. 9.19, в, ось балки изгибается также по окружности с кривизной.

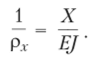
Если теперь учесть, что в исходном состоянии углы поворота в заделках равны нулю, то, наложив окружности, получим прямую линию. Из этого следует, что p_f = р_х. Приравняв приведенные выражения для данных величин, получим.

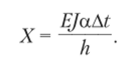
Таким образом, при неравномерном нагреве стержень, заделанный двумя концами, испытывает чистый изгиб, при этом ось стержня остается прямой, а растянутое волокно расположено со стороны действия меньшей температуры.

Применяя метод сил, также легко решить задачу для стержня с заделкой на одном и шарниром на другом конце. В табл. 9.3 приведены справочные данные для двух случаев закрепления концов стержня. Этими данными рекомендуется пользоваться при решении конкретных задач.

Таблица 93

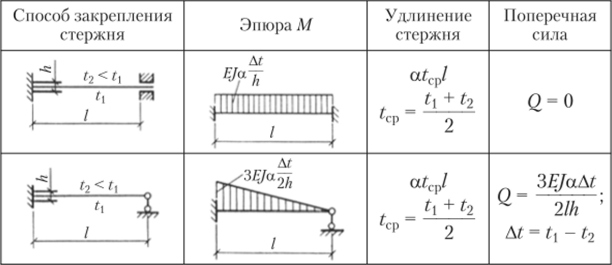
а — температурный коэффициент линейного расширения; h — высота поперечного сечения.

При построении эпюры моментов М_г в основной системе необходимо учитывать значения моментов не только в том стержне, который подвергается действию температуры, но также и в других стержнях, которые будут деформироваться при смещениях плавающих заделок от удлинения стержня на величину /, которая определяется по формуле / = а?_ср/.

Реакции R_jt, i= 1,2,/?, входящие в канонические уравнения, определяются так же, как при расчете на действие нагрузки, путем вырезания узлов или частей рамы в основной системе.

При решении канонических уравнений эпюра изгибающих моментов М_г строится в соответствии с формулой.

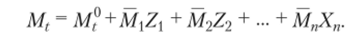
Рассмотрим пример, по которому можно проследить технику решения задачи. На рис. 9.20, а показана рама при действии температур t = 20 °C и ?₂ ⁼ -8°С. Длины / и жесткости EJ всех стержней одинаковы. Высота сечений для всех стержней равна h = 0,1/. Находим значения средних температур и их разности: 1) для обоих ригелей t_c? = (20 — 8)/2 = 6 °C; At = 28 °C; 2) для левой стойки t_cp = 20 °C; At = 0; 3) для правой стойки ?_ср = б°С; At = 28 °C.

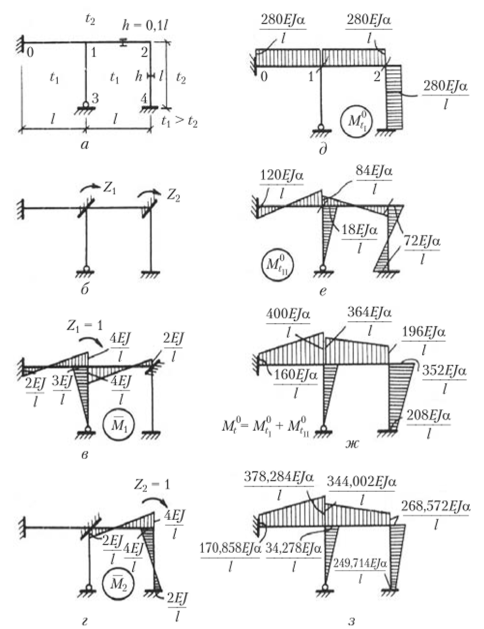
Puc. 9.20.

Наиболее трудной частью решения является построение эпюры моментов от температуры М, в основной системе. Выполним его в два этапа: на первом этапе не будем учитывать удлинения стержней от средней температуры и построим эпюру М°. На втором этапе построим эпюру М® от удлинения стержней при средней температуре.

Эпюра М® (рис. 9.20, Э) строится для каждого стержня в отдельности в соответствии с табл. 9.3. Для горизонтальных элементов и правой стойки разность температур Г одинакова и равна 28 °C. По табл. 9.3 для стержня, заделанного двумя концами, эпюра имеет вид прямоугольника с ординатой.

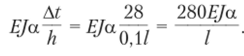
Для левой стойки t = 0, поэтому в ней эпюра отсутствует.

Для построения эпюры (рис. 9.20, е) необходимо учесть относительное смещение концов стержней в основной системе. Рассмотрим каждый стержень отдельно (см. рис. 9.20, а).

Стержень 0—1. Правая заделка смещается вверх на величину удлинения стойки 1—3 от t = 20 °C. Смещение это будет 20а/. В соответствии с табл. 9.1 от единичного смещения концов моменты равны 6EJ/I², а от смещения, равного 20а/, моменты будут 120EJ/1².

Стержень 1—2. Левая стойка удлиняется на 20а/, а правая на 6а/; относительное смещение заделок стержня 1—2 будет 20а/ - 6а/ = 14а/. Поэтому моменты на концах стержня будут 14а/(6?у)//² = 8AEJa/l.

Стержень 1—3. Верхний узел сместится вправо на величину удлинения ригеля 0—1, которая равна at_C[)l = 6а/. При смещении заделки на Z = 1 для стойки с шарниром на другом конце момент равен 3EJ/1², а от смещения 6а/ момент будет 18?/а//.

Стержень 2—4. Смещение верхнего узла будет равно сумме удлинений двух стержней 0—1 и 1—2 от средней температуры ?_ср; моменты на концах стойки 2—4 будут равны 6а (/ + 067У//² — 726EJ/I.

Эпюры М_х и М₂ от поворота заделок на углы Z = 1 и Z₂ = 1 изображены на рис. 9.20, в и г. Эпюра М® построенная по табл. 9.3, приведена на рис. 9.20, ж. _ _

Последовательно вырезая узлы 1 и 2, по эпюрам М_{ и М₂ находим матрицу реакций.

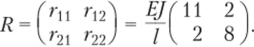
Вырезая те же узлы, по эпюре А/, (см. рис. 9.20, ж), находим.

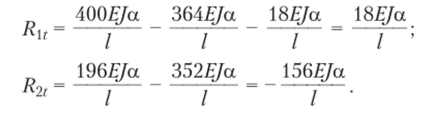
Вектор R, равен.

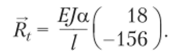
Матричное уравнение (после сокращения на EJ/1) можно записать в виде.

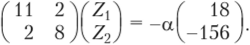
Обратная матрица.

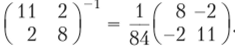
Поэтому.

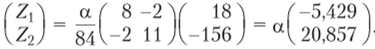
Умножив М| на Z|, а М₂ на Z₂ и сложив их с М, получим.

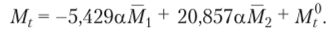
Пользуясь этой формулой, получим все ординаты окончательной эпюры M_t (рис. 9.20, з). Легко проверить, что в каждом узле имеется равновесие. Сумма моментов в стержнях, сходящихся в узел, равна нулю.