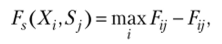Принятие решений с использованием принципа Сэвиджа и оценок альтернатив, заданных в количественной шкале

Метод предназначен для принятия решений с использованием принципа Сэвиджа для согласования оценок альтернатив, формируемых единственным экспертом с позиций единственного интегрального признака в различных проблемных ситуациях, с заданием предпочтений в количественной шкале. Обозначение метода в ЭСППР — SAVAGE.

В качестве возможных вариантов решения рассматривается набор из I альтернатив X = (Х_х, Х₂,…, X,…, X,), i = 1, 2,I.

Решение принимается при наличии / проблемных ситуаций 5 = (5), S₂, -, Sj…Sj), j = 1, 2,.

Оценка производится в количественной шкале, т. е. чем предпочтительнее альтернатива — тем больше балл, присваиваемый экспертом. В результате формируется матрица предпочтений размерности / xj, где I — количество возможных вариантов решения (альтернатив),/ — количество проблемных ситуаций. Элемент матрицы предпочтений Fпредставляет собой оценку варианта решения X, в у-й проблемной ситуации, выраженную в количественной шкале (/ = 1, 2,… /; у - 1, 2,…,./).

Алгоритм решения задачи предусматривает выполнение следующих шагов.

Шаг 1. Формирование матрицы сожалений. На данном шаге формируется матрица сожалений с элементами F_s(X_r Sj), характеризующая недополучение выигрыша из-за неопределенности в условиях принятия решения. Элементы матрицы сожалений вычисляются по правилу: для каждой у-й ситуации (у-го столбца матрицы предпочтений) определяется максимальное по всем альтернативам значение функции предпочтения, из которого затем вычитаются элементы рассматриваемого столбца матрицы предпочтений:

где Fjj — элемент матрицы предпочтений для z'-й альтернативы иу'-й ситуации (г = 1, 2,…, /;у= 1, 2,.

Шаг 2. Определение коэффициентов максимального сожаления альтернатив. На данном шаге для всех рассматриваемых альтернатив определяются коэффициенты максимального сожаления /у (г = 1, 2,…, Г) по формуле.

где F_s(Xj, Sj) — элемент матрицы сожалений для г-й альтернативы ву-й ситуации (г = 1- 2,…, /;у = 1, 2,…,./).

Шаг 3. Ранжирование альтернатив. На данном шаге альтернативы упорядочиваются по возрастанию коэффициентов максимального сожаления Fj (г — 1, 2, …, /). Альтернатива с наименьшим значением коэффициента F, считается наиболее предпочтительной и получает ранг 1, альтернативе со вторым, но величине значением коэффициента F, присваивается ранг 2 и т. д.

Таким образом, оптимальной считается альтернатива, определяемая критерием Сэвиджа:

где F_s (Xj, Sj) — элемент матрицы сожалений для г-й альтернативы в j-й ситуации (г = 1, 2,…, I;j = 1, 2,…,/);

Fj — коэффициент максимального сожаления i-й альтернативы (г = 1, 2,.

… I).