Изучение вариации. 
Демография и социальная статистика

Вариацией признака называется различие индивидуальных значений признака внутри изучаемой совокупности в один и тот же момент или период времени. Если средняя арифметическая, мода, медиана характеризовали положения, определяющие положение центра эмпирического распределения, то показатели вариации характеризуют рассеяние или отклонение признака от среднего значения. Показатели вариации можно классифицировать по способу расчета: линейные и квадратичные, и те и другие могут быть абсолютными, средними и относительными.

Размах вариации представляет собой разность между максимальной и минимальной величиной признака:

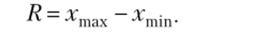
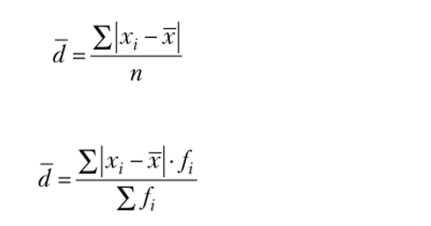
Среднее линейное отклонение (d) — это средняя величина отклонений вариантов признака от их среднего значения. Оно вычисляется по формуле средней арифметической, в зависимости от наличия частот в ряду распределения:

• — простое;
• — взвешенное, где x_i — х — абсолютные значения отклонений относительных вариант х, от средней арифметической х.

Среднее квадратическое отклонение обозначается через, а и рассчитывается по формулам для несгруппированных данных и для вариационных рядов соответственно:

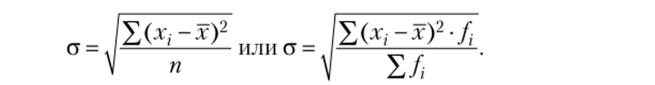
Квадрат среднеквадратического отклонения называется дисперсией и вычисляется по формуле.

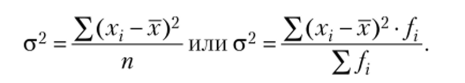aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">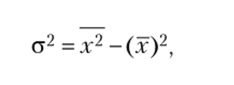

Возведя в квадрат правую часть равенства и разделив почленно на получим другую формулу для вычисления дисперсии, более удобную для использования: где х² — средняя величина квадратов вариантов; (х)² — квадрат средней арифметической.

Дисперсия о² является мерой вариации. Среднее линейное отклонение используется для вычисления среднего относительного отклонения:

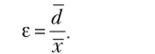
Коэффициент вариации V₀, представляющий процентное отношение среднеквадратического отклонения к средней арифметической, позволяет производить сравнительный анализ вариации в разных совокупностях:

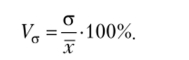
Величина этого показателя позволяет судить об интенсивности вариации признаков совокупности. Чем больше его величина, тем больше разброс значений, тем менее однородна совокупность по своему составу и тем менее представительная средняя.

Существует шкала определения степени однородности совокупности в зависимости от значений коэффициента вариации: если коэффициент вариации меньше 30%, то совокупность считается однородной, если коэффициент вариации лежит в пределах от 30 до 60%, то степень однородности средняя, если коэффициент вариации 60% и выше, то совокупность считается неоднородной.

Правило сложения дисперсий и виды дисперсий. Рассмотрим некоторую совокупность единиц и выберем признак, по которому разделим исследуемую совокупность на определенные группы. В этом случае можно говорить об общей вариации определенного показателя по всей совокупности, о вариации внутри выделенных групп и о вариации между группами, удовлетворигощих соотношению.

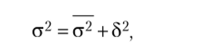
где а² — общая дисперсия по всей совокупности; 8² — межгрупповая дисперсия, характеризующая систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием факторного признака, который положен в основу группировки. Формула вычисления для нее:

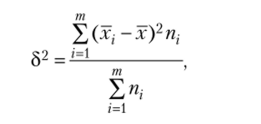
где т — число выделенных групп; n_t — число единиц в каждой группе; х, — — групповые средние.

Величина а² — средняя из внутригрупповых дисперсий а², отражающих случайную вариацию, г. е. часть вариации, которая происходит под влиянием неучтенных факторов и не зависит от факторного признака, положенного в основание группировки. Она вычисляется по формуле.

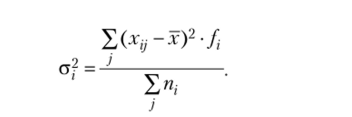
Средняя из внутригрупповых дисперсий исчисляется по формуле.

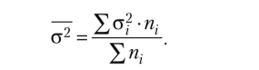
Вычисляют показатель эмпирического коэффициента детерминации р², который показывает долю общей вариации изучаемого признака, обусловленной вариацией группового:

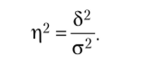
Извлекая квадратный корень из этого выражения, получим величину, называемую эмпирическим корреляционным отношением.

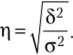
Это отношение характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака. Эмпирическое корреляционное отношение изменяется в пределах 0 < r| < 1. Если ц = О, то группировочный признак не влияет на результативный. Если ц = 1, то результативный признак изменяется только в зависимости от группировочного признака. Промежуточные значения оцениваются в зависимости от их близости к предельным.

Заметим, что совокупность разбивается на группы по факторному признаку. Групповые средние и дисперсии рассчитываются по каждой группе для результативного показателя.

Покажем правило сложения дисперсий на примере 2.1. Разобьем имеющиеся данные на три группы в зависимости от стажа работы по данным табл. 2.8. Результаты представлены в табл. 2.9.

Таблица 2.9

Данные распределения работников на группы в зависимости от стажа работы.

Воспользуемся исходными данными табл. 2.8, где х = 3440 у.д.е., и рассчитаем основные показатели вариации. Результаты оформлены в табл. 2.10.

1. Среднее линейное отклонение.

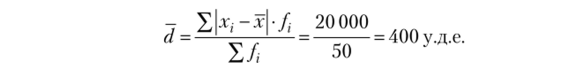
2. Дисперсия.

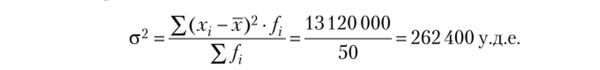
3. Среднее квадратическое отклонение.

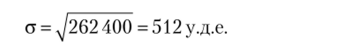
Таблица 2.10.

Расчет показателей вариации.

4. Коэффициент вариации.

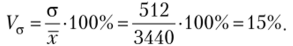
Рассчитаем групповые средние и дисперсию:

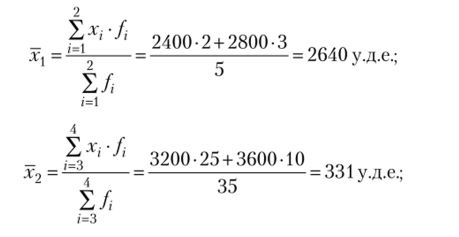
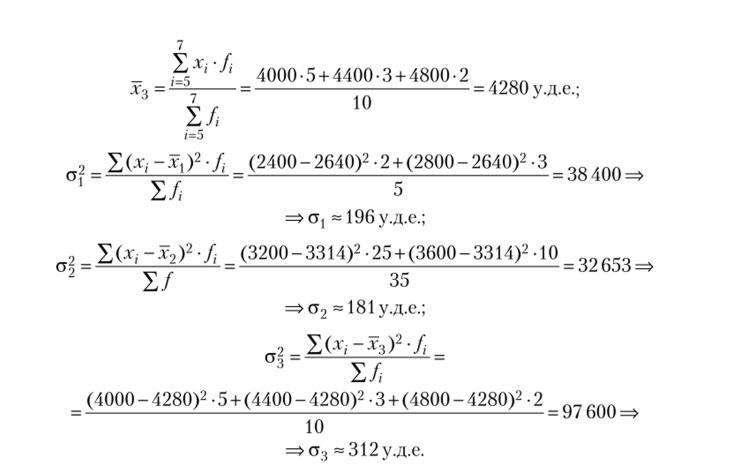
Рассчитаем среднюю из внутригрупповых дисперсий:

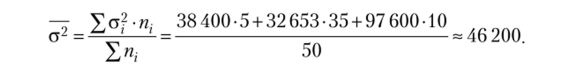
Рассчитаем межгрупповую дисперсию (общее среднее, но всей совокупности известно: х = 3440 у.д.е.:

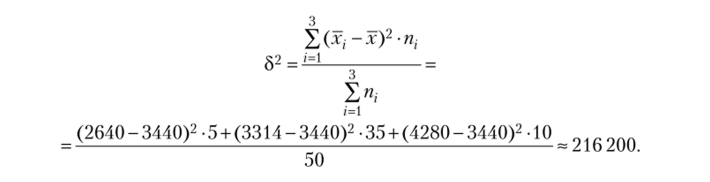
Общая дисперсия: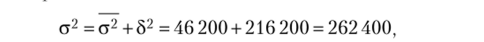

что совпадает с рассчитанной дисперсией по всей совокупности. Эмпирическое корреляционное отношение:

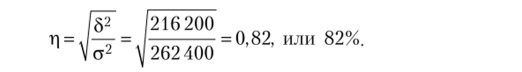
Таким образом, факторный признак — стаж работы, обусловливает размер заработной платы работников на 82%, на долю не учтенных факторов приходится 12%.

Закономерности распределения. Можно заметить, что существует определенная зависимость между изменением значений вариационного признака и частоты. Частота увеличивается с возрастанием значения признака, а после достижения максимальной величины в середине ряда начинает уменьшаться. Это говорит о некотором закономерном изменении частоты в зависимости от варьирующего признака. Такие закономерности изменения частоты в вариационном ряде называются закономерностью распределения.

Задачей анализа вариационных рядов является выявление закономерности распределения частот в виде непрерывной линии. Из математической статистики известно, что, увеличивая объем совокупности и уменьшая интервал группировки, графически изображенные данные в виде полигона или гистограммы распределения будут приближаться к некоторому пределу в виде плавной линии. Это и будет кривая распределения, выражающая функциональную зависимость между изменением частоты и изменением варианты.

Различают кривые распределения одновершинные (симметричные, асимметричные), многовершинные. Одновершинность характерна для однородных совокупностей, многовершинность говорит о неоднородности изучаемой совокупности.

Для изучения формы распределения рассчитывают X, Mo, Me, вычисляют показатель асимметрии A_s (показатель Пирсона) по формуле.

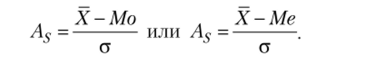
Его величина может быть положительной и отрицательной: если A_s > О, то форма распределения имеет правостороннюю асимметрию; если A_s < 0 — то левостороннюю асимметрию. При правосторонней асимметрии выполняется неравенство X > Me > Мо, а при левосторонней — X < Me < Мо.

Оценить асимметрию можно с помощью отношения центрального момента распределения третьего порядка к среднему квадратическому отклонению в кубе, т. е.

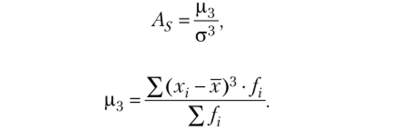
где В общем виде центральный момент k-i o порядка называется выражение вида.

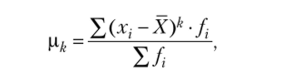
тогда центральные моменты первых четырех порядков имеют вид.

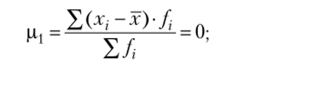
Принято считать, что если показатель асимметрии выше 0,5 (независимо от знака), то асимметрия значительная; если она меньше 0,25 — то незначительная. Оценка существенности Л5 производится па основе средней квадратической ошибки коэффициента асимметрии а,., которая зависит от числа наблюдений и рассчитывается по формуле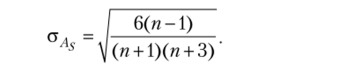

ш В случае ¹->3 асимметрия существенная, и распределение признака в генеральной совокупности не симметрично. В противном случае асимметрия несущественная, и ее наличие вызвано случайными обстоятельствами.

Для симметричного распределения исследуют форму вершины распределения. Для этого рассчитывают показатель эксцесса Е_х по формуле.

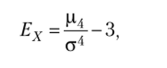
?(*, — -г)¹

II

где М-4 =.

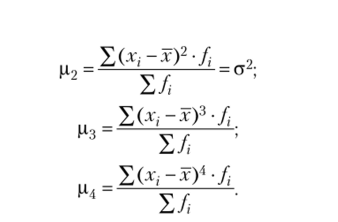
— центральный момент четвертого порядка.

Если Е_х = 0, то распределение нормальное, если Е_х > 0 — то более островершинное, если Е_х < 0 — то более плосковершинное.

Таким образом, изучение вариации сводится к определенному алгоритму действий: построение вариационного ряда; графическое изображение в виде гистограммы, полигона, кумуляты; расчет показателей центра распределения и структурных характеристик вариационного ряда; расчет показателей размера и интенсивности вариации; оценка вариационного ряда на асимметрию и эксцесс.

Выравнивание вариационных рядов. Теоретическое распределение имеет определенную аналитическую формулу или выражение, содержащее некоторые параметры, которые определяются исходя из данных эмпирического распределения. Поэтому выравнивание вариационного ряда — это значит найти выражение теоретического распределения такое, которое наименьшим образом отличалось бы от эмпирического.

Рассмотрим два вида теоретических распределений: нормальное распределение и распределение Пуассона. Есть и другие, например, биноминальное распределение и т. п. Но это выходит за рамки данного учебника, так как каждое из распределений имеет свою специфику и свою область применения.

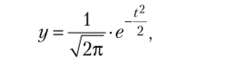
х — X

где у — ордината кривой нормального распределения; t =—нормиро;

ст ванные отклонения.

Графическое изображение кривой нормативного распределения показано на рис. 2.7. Видно, что ось х является асимптотой, а точки перегиба имеют абсциссы на расстоянии ст от центра симметрии.

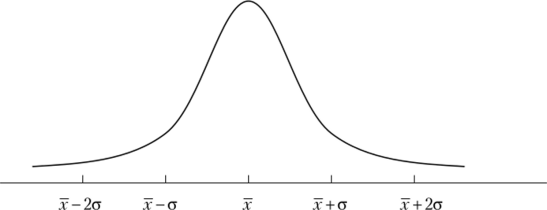
Рис. 2 7. Кривая нормального распределения.

При выравнивании по аналитическим формулам необходимо вычислить теоретические частоты исходя из эмпирических частот. Если выравнивание производится согласно нормальному закону распределения, то расчеты производят по формуле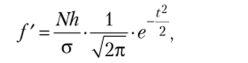

где N = Yjfi — сумма всех частот вариационного ряда; h — величина ингер;

х — х

вала в группах; а — среднеквадратичсскос отклонение; t =-— нормиро;

а ванное отклонение вариантов от средней арифметической.

Значение функции ф(t) = —;=e 2 загабулировано (см. таблицу прило;

у2л жен ия 1).

Распределение Пуассона имеет аналитическое выражение вида.

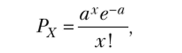
где Р_х — вероятность наступления отдельных событий х, а-х — средняя арифметическая ряда.

Если в дискретном вариационном ряду наблюдается резкое уменьшение частоты при возрастании значений признака, а средняя ряда приблизительно равняется дисперсии, то следует производить выравнивание по кривой Пуассона (рис. 2.8).

Рис. 2.8. Кривая Пуассона.

В этом случае теоретические частоты определяются по формуле 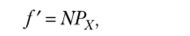где N — общее число единиц ряда.

Найденные теоретические частоты необходимо сравнить с их эмпирическими значениями и оценить расхождения между ними, которое позволит подтвердить или опровергнуть правильность выдвинутой гипотезы о наличии определенного характера распределения в эмпирическом ряду.

Оценить близость / и /' позволяют критерии согласия, к которым относятся критерий х^2 — хи-квадрат (критерий К. Пирсона) и критерии В. И. Романовского и А. Н. Колмогорова.

Критерий х² хи-квадрат выражается суммой отношений квадратов расхождений между/и /' к теоретическим частотам /' в виде формулы.

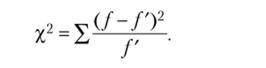
Рассчитанное таким образом фактическое значение критерия сравнивается с критическим (табличным), определяемым по специальным таблицам. Входом в таблицу являются уровень значимости а и число степеней свободы К. Уровень значимости а, как правило, равен 5% или 1% и представляет собой вероятность допустить ошибку в предположении о законе распределения.

Число степеней свободы К представляет разность между числом групп т в ряду распределения минус 1 и числом параметров эмпирического распределения, по которому рассчитываются теоретические частоты. В случае нормального распределения К = т — 3.

Оценка случайности расхождений между частотами / и /' по критерию Романовского рассчитывается по формуле.

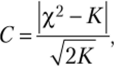
где х² — критерий Пирсона; К — число степеней свободы.

Для С < 3 расхождения считают случайными.

Критерий Колмогорова (X) определяется по формуле.

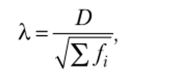
где D — максимальное значение между накопительными частотами / и /'; X — сумма эмпирических частот.

Необходимым условием применения этого критерия является достаточно большое число наблюдений (не менее 100). Рассчитав X, но специальным таблицам вероятностей Р (X) находим соответствующие значения вероятности Р (х). Если оно близко 1, то это означает, что с вероятностью, близкой к 1, можно утверждать, что отклонения эмпирических частот от теоретических являются случайными.

Задача 2.1. На ниточно-прядильном комбинате проводят испытания на прочность ниток. Эта процедура заключается в подвешивании гирек различной массы к ниткам. Было произведено 200 испытаний, распределение числа которых по массе представлено в табл. 2.11 (графы 1 и 2). Необходимо произвести выравнивание эмпирического распределения и оценить расхождения между частотами / и /' при помощи критериев согласия.

Таблица 2.11

Решение. Наблюдая плавное изменение распределения числа испытаний (графа 2) от минимального значения к максимальному и опять к минимальному, можно выдвинуть гипотезу о нормальном законе распределения. Значит, выравнивание будем производить, но кривой нормального распределения. Тогда теоретические частоты находятся, но формуле.

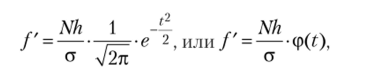
х — X _.

где t —-нормированные отклонения от средней, т. е. х и ст — основные а.

параметры кривой нормального распределения.

• 1. Рассчитаем параметры нормального закона распределения х и ст исходя из эмпирических данных. Для этого найдем середины интервалов (графа 1) и запишем в графу 3. Используя известные формулы, вычислим среднее значение вариантов х и их среднеквадратическое отклонение ст, получим х = 161,4 и, а = 13.
• 2. Найдем отклонения каждого среднего варианта (графа 3) от среднего значения х и запишем в графу 4.

х — X

3. Вычислим нормированное отклонение t =-, запишем в графу 5.

о.

4. Найдем табличные значения функции cp (f) по известным значениям t (см. таблицу приложения 1), запишем в графу 6.

" «» Nh 20 010.

5. Рассчитаем постоянный множитель — = ——— = 154.

ст 13.

6. Найдем теоретические частоты 154 ф (?) = /', результат округляем до целых и записываем в графу 7.

Из табл. 2.11 очевидно, что, несмотря на отдельные расхождения, теоретические частоты (/') близки к эмпирическим (/). Чтобы оценить, случайны или нет эти расхождения, воспользуемся критериями согласия.

Оценку будем производить по критерию Пирсона:

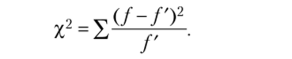
Все необходимые расчеты, исходя из формулы, представлены в табл. 2.12.

Таблица 2.12

Расчет критерия Пирсона.

Согласно представленным расчетам для нашего примера критерий X² = 0,71. Теперь его значение нужно сравнить с табличным. Входом в таблицу является уровень значимости, а и число степеней свободы К. Пусть уровень значимости, а = 0,05 (5%). Ряд распределения в нашем примере имеет восемь групп частот. Отсюда К = 5. Теперь определим табличное значение критерия х² по таблице приложения 2.

Для нашего примера табличное значение х^2 — критерия Пирсона %²_аб_л = 11,07. Фактическое значение Хф_аКт ⁼ 0,71 меньше табличного, что доказывает случайность расхождения между частотами / и/ и гипотезу о близости эмпирического распределения к нормальному.

В отсутствие вероятностных таблиц можно применить критерий Романовского:

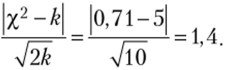
Расчеты показывают, что значение критерия Романовского равно 1,4. Отсюда делаем вывод о случайных расхождениях между частотами. Для проверки нашей гипотезы рассмотрим критерий Колмогорова.

' D

A, = —j=. Рассчитаем накопленные частоты /и /'. Найдем максимальную V VN)

разницу между ними. Результаты представим в табл. 2.13.

Таблица 2.13

Результаты расчетов.

Из таблицы очевидно, что максимальная разница D = 2, отсюда D 2.

А = -j= = — = 0,14. Теперь найдем значение вероятности Р (А) по таблице приложения 3. Получаем, что при, А = 0,14 Р = 1,000. Делаем вывод, что с вероятностью, равной единице, расхождения между / и /' случайны.

Задача 2.2. На заводе в течение шести рабочих дней наблюдали работу 50 станков, производящих высокоточное оборудование Остановка станков квалифицировалась как неисправность, которую необходимо устранить. Вес неисправности регистрировались в таблице, имеющей следующий вид:

Необходимо с помощью критериев согласия оценить близость эмпирических и теоретических частот.

Решение. Наш частотный ряд представляет собой распределение по дискретному признаку. Заметим, что частота резко уменьшается при увеличении значения признака. Поэтому выдвигаем гипотезу: число неисправностей подчиняется закону Пуассона.

а^хе~^а

Для нахождения Р_х =-;—, необходимо рассчитать среднее число неис;

х!

правностей: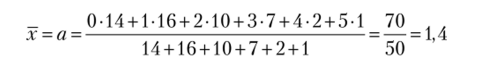

и вычислить значение е~¹⁴ = 0,2466. Тогда вероятность имеет вид.

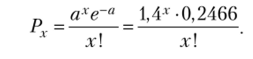
Подставляя в эту формулу последовательно х = 0, 1, 2, 3, 4, 5, получим вероятности числа неисправностей от 0 до 5. Теоретические частоты вычисляем по соответствующей формуле.

Расчеты Р_х и/' (округленные до целого числа) представлены в табл. 2.14.

Таблица 2.14

Значения Р_х и f

Разность частот / и /' оценим по трем критериям: Пирсона, Романовского и Колмогорова.

Расчеты критерия Пирсона X² = X—у, — представлены в табл. 2.15.

Расчеты критерия Пирсона.

Фактическое значение критерия Пирсона %|_aKT⁼0,89 сравниваем с табличным значением Х?_абл ⁼ ^>49 (входом в таблицу является К = 6−2 = 4 и, а = 0,05). Поскольку %|_aKT — Х?_абл> ^т-^е— 0−89 < 9,49, делаем вывод, что расхождения между частотами / и /' случайны и выдвинутая гипотеза верна.

x²-k |l-4|.

Вычислим значение критерия Романовского: < 3. Отсюда делаем вывод — расхождения случайны.

Аналогично, как и в задаче 2.1, рассчитаем критерий Колмогорова D 2 2.

А. = —j= — —г= — —= 0,3. Согласно таблице приложения 3 находим Р (Х ~ Viv л/50 А 07.

— 0,3) — 1.

Таким образом, согласно всем трем критериям, расхождения между частотами в эмпирическом и теоретическом ряду случайны, и имеет место рас п ределсн ие IIуассона.

Выборочное наблюдение — это разновидность несплошного статистического наблюдения, при котором обследуется только часть единиц изучаемой совокупности, отобранных определенным способом.

Применение выборочного метода обосновывается тем, что в ряде случаев провести сплошное наблюдение практически невозможно и экономически нецелесообразно (например, оценка качества продуктов питания, обследование бюджетов семей).

Сплошное наблюдение больших совокупностей (фермерские хозяйства, домохозяйства, предприятия, группы населения) требуют огромных материальных, финансовых и организационных затрат. Применение выборочного метода позволяет значительно сэкономить время, силы и средства, что имеет немалое значение. Выборочное наблюдение помогает ускорить получение необходимой информации. При обследовании 10% единиц совокупности времени будет затрачено меньше, а результаты будут получены быстрее и иметь более актуальное значение. Фактор времени важен в условиях изменяющейся социатьной ситуации. Кроме того, результаты выборочного обследования имеют большое значение для уточнения и проверки сведений сплошных наблюдений.

Совокупность единиц, отобранных для обследования, называется выборочной, или выборкой. Совокупность единиц, из которой производится отбор, называется генеральной.

Насколько выборка репрезентативна, настолько качественные результаты выборочного обследования будут получены.

Цель выборочного наблюдения заключается в оценке параметров генеральной совокупности (х, р) при использовании значения выборочной средней х и выборочной доли со. Разница между генеральными (х, р) и выборочными (х, со) параметрами называется ошибкой репрезентативности. Избежать таких ошибок невозможно, но их можно вычислить по известным формулам теории вероятностей и математической статистики, в зависимости от способа и вида отбора.

Выборочные наблюдения делятся по видам (индивидуальный отбор — выборка состоит из отдельных единиц генеральной совокупности; групповой — рассматриваются группы единиц; комбинированный — сочетание первого и второго), методам (повторный и бесповторный) и способам отбора, определяющим процедуру выбора единиц из генеральной совокупности. Различают собственно-случайную, механическую, типическую, серийную и комбинированную выборки. В исследованиях социальных явлений обычно применяют бесповторный отбор.

Зная способ отбора, можно определить ошибку выборки: Д* = |х-х|. Средняя, или стандартная, ошибка для средней величины Ц_; при случайном и механическом отборе рассчитывается по следующим формулам:

при повторном отборе — 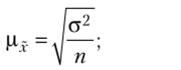при бесповторном отборе —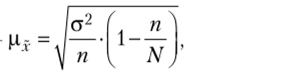

где а² — дисперсия признака в генеральной совокупности; п м N — объем выборки и генеральной совокупности соответственно.

Сопоставляя эти выражения, можно заметить, что они отличаются множителем, который всегда меньше единицы. Отсюда следует, что бесповторный отбор дает меньшую ошибку выборки.

Отметим, что дисперсия признака в генеральной совокупности обычно неизвестна. Ее можно заменить выборочной дисперсией of, так как доказано, что соотношение между а§ и о| определяется равенством.

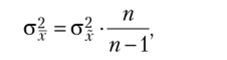
где величина второго сомножителя при большой численности выборочной совокупности (п —> °о) стремится к единице. Тогда можно считать, что выборочная дисперсия приближенно равна генеральной, т. е. ст| «о|.

Аналогичное утверждение имеется для дисперсии доли о² в генеральной совокупности.

Расчет средней ошибки выборочной доли для повторного и бесповторного отборов определяется соответственно формулами.

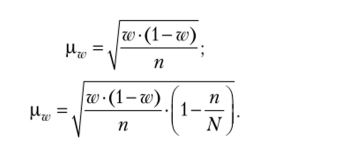
Предельная ошибка выборки Д₅.(Д_да) определяется формулой t-кратной средней ошибки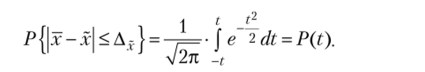

где t — коэффициент доверия, табличное значение которого определяется интегральной функцией Лапласа, при заданной доверительной вероятности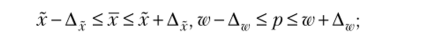

В табл. 2Л6 приведено соответствие значений коэффициента доверия t уровням доверительной вероятности.

Таблица 2.16

Уровни доверительной вероятности и соответствующие им значения t

Если известны значение выборочной средней признака х или доли w и предельная ошибка выборки Д* или Д_к" то доверительные интервалы для значений генеральных параметров имеют вид:

• для собственно-случайной и механической выборок.

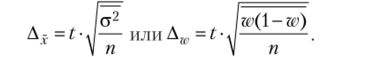
• для типической (районированной) выборки для определения доверительного интервала.

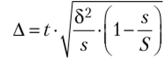
Здесь а² — средняя дисперсия, а ошибка выборки зависит от внутригрупповой вариации.

Серийная выборка, как правило, проводится бесповторная, и предельная ошибка выборки вычисляется по формуле.

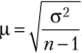
5^ (х-^_ х)^.

где 5² =—— межсерийная (межгрупповая) дисперсия; s — число отобранных серий; 5 — число серий в генеральной совокупности.

В случае малой выборки (п < 20) средняя ошибка вычисляется по формуле.

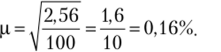
Для построения доверительных интервалов показателя генеральной совокупности используют таблицы вероятности Стыодснта, где Р = S (t, n) определяется в зависимости от объема выборки и t.

Задача 2.3. Методом собственно-случайной выборки обследованы 100 коров на жирность молока. Средняя жирность молока по результатам выборочного обследования равна 3,64%, а дисперсия — 2,56.

Необходимо определить: 1) среднюю ошибку выборки; 2) с вероятностью, равной 0,954, предельные значения генеральной средней.

Решение. 1. Зная формулу средней ошибки выборки р = J— и извест;

V п

ные из условия задачи значения п = 100, о² = 2,56, сразу находим.

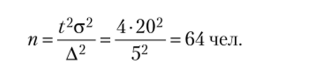
2. Воспользуемся формулой предельной ошибки, А = ?р, и по заданной вероятности Р = 0,954 найдем t = 2 (см. табл. 2.16) и, подставив в формулу предельной ошибки, получим, А = 2 • 0,16 = 0,32, а поскольку х = х± А => 3,32% <�х< 3,96%.

Задача 2.4. Сколько рабочих завода нужно обследовать (случайная выборка), чтобы для определения средней заработной платы, с вероятностью, равной 0,954, можно было бы гарантировать ошибку не более 5 руб. Среднее квадратичное отклонение а = 20 руб.

fa²" .

Решение. Определить п можно сразу из формулы, А = ?,—:

V п

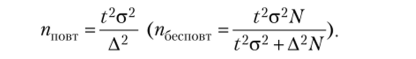
В ряде случаев для выборочного наблюдения встает вопрос о необходимой численности выборки для точности расчета оценок параметров генеральной совокупности. На практике расчет объема выборки производят по формуле для случайного повторного (бесповторного) отбора: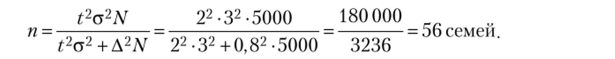

Очевидно, что объем выборки обратно пропорционален квадрату предельной ошибки и прямо пропорционален дисперсии признака и величине t².

В некоторых случаях исследователь задает величину допустимой предельной ошибки и уровень вероятности, обеспечивающий точность оценок будущей выборки. Для оценки дисперсии в генеральной совокупности можно использовать: либо выборочную дисперсию из прошлых данных или пробных обследований; либо дисперсию, найденную из соотношения для среднеквадратического отклонения: о =—х; либо дисперсию, определенную из соотношения для асимметрического распределения; либо дисперсию, вычисленную из соотношения для нормального распределения:

¹ р ;

а-—К, где х — среднее значение признака в генеральной совокупности,.

R — размах вариации. Для оценки генеральной дисперсии доли используют максимально возможную дисперсию альтернативного признака о²₍₀._ш тах = = 0,5−0,5 = 0,25.

Задача 2.5. Пусть обследовано 5000 семей (выборка случайная бесповторная). Предлагается найти средний размер семьи при условии, что с вероятностью 0,954 и при среднеквадратическом отклонении 3,0 чел. ошибка выборочной средней не превышает 0,8 чел. (ошибка и среднее квадратичное отклонение определены на основе пробного обследования).

Решение. При Р (?) = 0,954; t = 2 необходимая численность выборки находится по формуле.

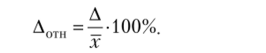
Итак, для того чтобы с вероятностью 0,954 гарантировать, что ошибка определения среднего размера семьи не превысит 0,8 чел., необходимо обследовать 56 семей.

Иногда, на практике задается не абсолютная величина предельной ошибки выборки, а ее относительный уровень — отношение предельной ошибки выборки к среднему значению признака, выраженных в процентах. Эта величина называется относительной ошибкой выборки и характеризует относительную погрешность выборочного наблюдения:

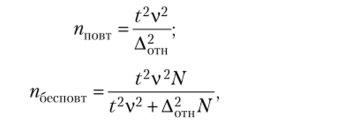
Расчет объема выборки при заданном уровне относительной ошибки осуществляется по формулам.

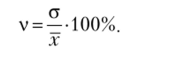
где v — коэффициент вариации,.

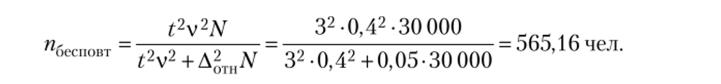
Задача 2.6. Па бирже груда состоит на учете 30 тыс. безработных. Чтобы определить величину средней продолжительности безработицы, проводится выборочное обследование. Коэффициент вариации продолжительности безработицы по прошлогодним данным составляет 40%. Чему должен равняться объем выборочной совокупности, чтобы с вероятностью 0,997 утверждать: полученная предельная ошибка выборки не превышает 5% средней продолжительности безработицы?

Решение. Доверительной вероятности P (t) = 0,997 соответствует t = 3. Для расчета численности выборки воспользуемся формулой.

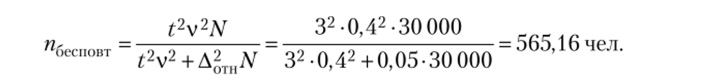
(объем выборки округляют только в большую сторону).

Таким образом, объем выборки должен составлять 566 безработных, чтобы с вероятностью 0,997 можно было утверждать: полученная ошибка не превышает 5% средней продолжительности безработицы.