Основные теоремы теории вероятностей

В большинстве задач надежности определяются вероятности не простых случайных событий, а сложных, являющихся комбинацией элементарных (простых). Оценка их вероятности через известные значения вероятностей простых проводится путем применения основных теорем, которые формулируются на основании понятий, связанных с элементарными случайными событиями.

Теорема сложения вероятностей. Суммой п событий называется сложное событие, заключающееся в появлении хотя бы одного из п. Вероятность суммы п несовместных событий равна сумме вероятностей этих событий:

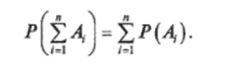
Если появление хотя бы одного из п несовместных событий является достоверным, то события Л/ составляют полную группу несовместных событий, для я.

которых выполняется соотношение Р (А_п)= ?/*(4) = 1. Сумма вероятностей ы.

противоположных событий: Р (А) + Р[А} -1. Если события А и В совместны, вероятность их суммы — Р (А + В) = Р (А) + Р (В)~ Р (АВ).

Вероятность суммы любого числа совместных событий:

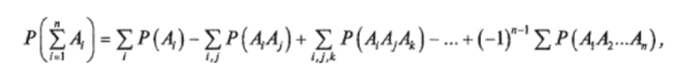
которая выражает вероятность суммы любого числа событий через вероятности произведений этих событий, взятых по одному /; по два /, j по три /, у, к и т. д.

Общая формула, выражающая вероятность произведения произвольного числа событий через вероятности сумм этих событий, взятых по одному, два, три и т. д., имеет вид:

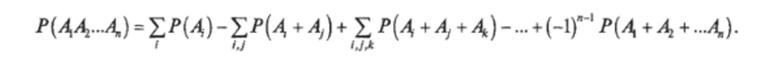
Пример. Элементы К и Кг схемы электроснабжения (рис. 7.8) резервируют друг друга. При отказе одного из них происходит автоматическое переключение на другой. Элемент Т не резервирован. Для того, чтобы отказала система, нужно, чтобы одновременно отказали оба элемента К и Aj или элемент Т Нарушение электроснабжения (событие Q представляется в виде: С = К_ХК₂ + Т, где К — отказ элемента К Ki~~ отказ элемента Ki Т— отказ элемента Т. Выразить вероятность события С через вероятности событий содержащих только суммы, а не произведения элементарных событий, Хь К2, Т.

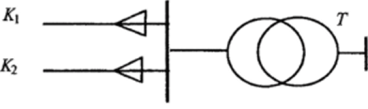
Рис. 7.S. Схема электроснабжения

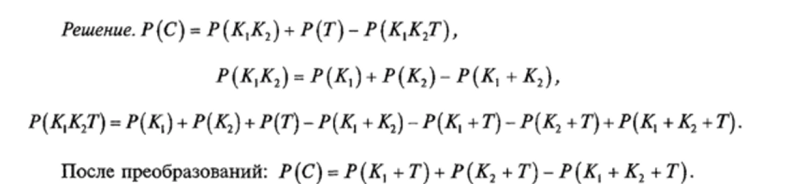
Теорема умножения вероятностей. Введем понятия событий независимых, зависимых и условной вероятности события. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет и зависимым, если вероятность события А меняется в зависимости от того, произошло ли событие В.

Пример. Отказ ЛЭП-1 и ЛЭП-2 разного напряжения, отходящих от разных источников и питающих разных потребителей, — независимые события; вероятность короткого замыкания на ЛЭП зависит от грозовой деятельности; вероятность отказа оставшегося в работе трансформатора на двухтрансформаторной подстанции зависит от величины нагрузки; вероятность повреждения оборудования подстанции зависит от повреждаемости в присоединенной сети.

Вероятность события А, вычисленная при условии, что имело место событие В_у называется условной вероятностью события А и обозначается Р (А В). Если события независимы, то.

Вероятность произведения независимых событий определяется как.

Пример. Технологический процесс предприятия обеспечивают 3 электродвигателя. Для каждого двигателя вероятность того, что он в данный момент работает, равна р — 0,6. Какова вероятность того, что в данный момент работает хотя бы один электродвигатель?

Решение. В данный момент могут произойти три независимых события: А — работает любой из трех один, или А — любые два, или Ат, — три двигателя. Если ни одно из этих событий не наступило, то говорят о совместном наступлении Однако следует учесть, что при большом количестве событий использование ее приводит к более громоздким вычислениям.

Пример. Вероятность отказа элемента СЭС равна q. Для повышения надежности предусмотрено т резервирующих элементов. Определить, во сколько к раз увеличится надежность системы, если под надежностью понимать ВБР.

Решение. Вероятность того, что откажут вес параллельные элементы (собы;

т тие A): Q (A) = YQi — Q^m- Вероятность того, что не откажет хотя бы один из па;

*" I.

раллельно работающих элементов (событие В) Р (В) = 1 — Q{A) = 1 —q^m. Надежность одного элемента R = 1 — q. Искомая величинг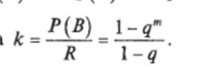

Если задана вероятность отказа элемента q, можно найти число резервных элементов т, при котором вероятность отказа системы Q не будет превосходить заданную величину, т. е. q^m <, Q. Тогда необходимая кратность резервирования определяется как т = Задавшись числом резервных элементов /л, можно Inq

определить, какой должна быть надежность каждого из них q = tfQ.

Пример. При относительно малых вероятностях повреждений, характерных для элементов ЭЭС (для силовых трансформаторов q = 0,01), увеличение надежности при двукратном т = 2 и трехкратном т = 3 резервировании составит.

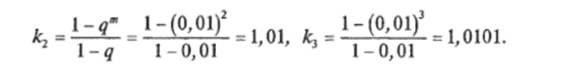
(произведении) противоположных событий Л, А₁, А_Ъ, сумма вероятностей которых равна: Р (Ау + А₁ + Л_у)+ Р[л_х A₁ i4jJ = l. По теореме умножения.

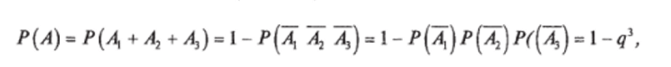
где q = 1 — р = 1 — 0,6 = 0,4. Искомая вероятность Р (А) = 1 — q³ = 1 — 0,4³ = 0,936. Эту же задачу можно решить с использованием теоремы сложения:

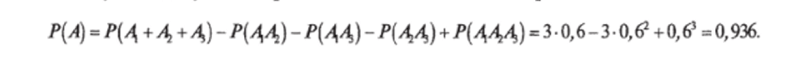
Если при q = 0,01 вероятность отказа двухтрансформаторной подстанции п ( лл 1 ln () 1п0,001 -6,9. _с г.

Q = 0,001, то т- = —-? = —- —- = 1,5 — необходимая кратность резерви;

q 1п0,01 -4,6.

рования. То есть число резервных элементов т = 2, что соответствует большинству СЭС. При заданной вероятности отказа системы Q = 0,001 и т = 2 допустимая вероятность отказа одного элемента q = ^Q =^0,001 = 0,003, что подтверждает целесообразность не более, чем двукратного резервирования.

Более подробное исследование вопроса повышения надёжности системы при помощи резервирования с учётом затрат на него рассмотрено в п. 9.5.

Вероятность произведения зависимых событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:

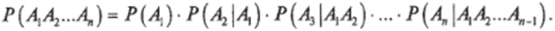
Пример. Вероятность отказа одного из трансформаторов в нормальном режиме работы (см. рис. 7.6, 6 />_т -0,01. Оставшийся трансформатор продолжает работу в режиме перегрузки и вероятность его отказа p_Tj =0,015. Какова вероятность отказа двух трансформаторов этой подстанции?

Решение. Второй трансформатор отказывает (событие В) при условии, что произошло событие А — отказ первого трансформатора. Вероятность совместного наступления этих событий Р (С) />© = Р (А)Р (В А) = 0,01 • 0,015 = 0,15.

Пример. Воздействие среды S на систему передачи и обработки информации N выражается в виде помех в каналах передачи информации, отказа и сбоев в работе аппаратуры, ошибок человека-оператора и т. п.

При проектировании и эксплуатации систем автоматики и телемеханики, релейной защиты и сигнализации, передачи данных, интеллектуальных активноадаптивных сетей должны учитываться различные причины (помехи, отказы, сбои, недостоверная входная информация, ошибки человека как звена системы, структурные и программные ошибки) и характер их влияния на показатель качества работы системы в целом. На рис. 7.9 дано структурное представление системы передачи информации с учётом воздействия как помех, так и отказов в работе аппаратуры.

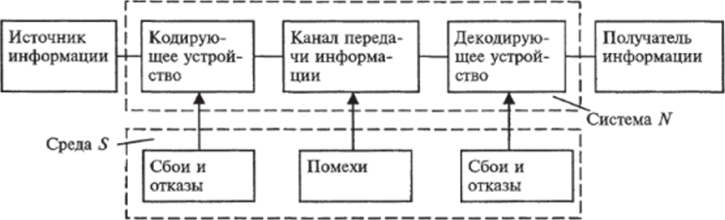
Рис. 7.9. Структурная схема передачи информации

Для оценки достоверности передачи данных можно использовать вероятность события, заключающегося в том, что реальная выходная информация совпадёт (в пределах заданной точности) с некоторым истинным значением РистЕсли предположить, что названные причины исчерпывают все возможные случаи, то Р_ист определяется как вероятность совместного наступления следующих событий:

А — возможные отказы и сбои в аппаратуре системы не привели к ошибкам в выходной информации;

В — действие помех не привело к ошибкам в выходной информации;

С — алгоритмические, программные и структурные ошибки не привели к ошибкам в выходной информации;

D — информация на выходе системы не имеет ошибок, несмотря на поступление недостоверной информации на входе системы;

Е — действия человека как звена системы не привели к появлению ошибок в выходной информации.

Вероятность правильного решения может быть вычислена как вероятность совместного наступления событий А, Я, С, Д Е:

где вероятности P (ABCDE), P (BCDE), P (CDE), P (DE), P (E) отнесены к одному и тому же интервалу времени, в качестве которого можно принять длительность передачи одного сообщения (кодовой комбинации).

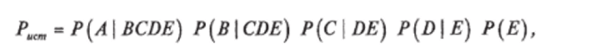
Если события Л, В_у Су D, Е независимы, что имеет место в большинстве практических случаев, то вероятность правильной передачи сигнала определяется как.

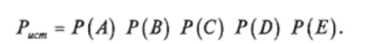
Формула полной вероятности. По ней определяется вероятность события А, которое может произойти совместно с одним из событий Я/, называемых гипотезами Я, Я₂,…, Я", образующих полную группу несовместных событий, т. е.,.

?/>(#,) = 1. Тогда м.

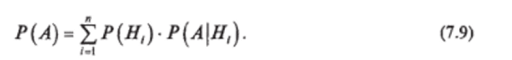
Пример. Работа крупного электродвигателя возможна при функционировании двух вспомогательных двигателей, обеспечивающих смазку и охлаждение основного. При нормальной работе вспомогательных двигателей основной отказывает с вероятностью q₂ при работе только двигателя смазки — с вероятностью q при работе только двигателя охлаждения — с вероятностью q₂ при отказе обоих вспомогательных электродвигателей основной отказывает с вероятностью <7оВероятность безотказной работы двигателя, смазки — р, а охлаждения — Р2- Найти вероятность безотказной работы основного двигателя.

Решение. Рассмотрим гипотезы: Н₂ ~ работают оба вспомогательных двигателя; Н[ - работает двигатель, обеспечивающий смазку основного; Н₂ ~ работает двигатель, обеспечивающий охлаждение основного; Но ~ оба вспомогательных двигателя вышли из строя и не работают. Вероятности этих гипотез:

В силу того, что слова «независимый» и «несовместный* в какой-то мере фонетически близки, их вероятностный смысл при решении практических задач часто путают. Поэтому необходимы дополнительные пояснения.

Предположим, что события А и В таковы, что Р (А)>0 и />(/?) >0. Если события А и В несовместны, то событие А п В невозможно и Р (АгВ) = 0. Но при этом выражение (7.7) не может иметь места и, следовательно, события А и В

не являются независимыми. Обратно, если события А и В независимы, т. е. выполняется (7.8), то Р (А п В) > 0 и поэтому события А и В не могут быть несовместными.

Пример. Схема системы показана на рис. 7.10. Система находится в работоспособном состоянии, если: а) работоспособны все элементы; б) работоспособны элементы 1 и 2 или 3 и 4, а элемент 5 может не работать; в) работоспособны элементы 1,5,4 или 3,5,2. Вероятности безотказной работы всех элементов одинаковы и составляют /?/=0,9. Требуется вычислить вероятность безотказной работы этой системы (вероятность события А).

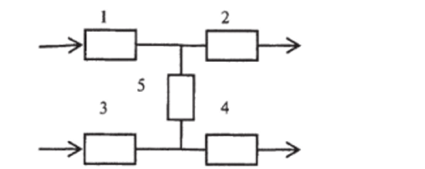
Рис. 7.10. Схема системы

Решение. Событие А подразделяется на несовместные события ВА и В^А, где В и Bi — события (гипотезы), соответствующие отсутствию или наличию отказа элемента 5. Очевидно, что р (В_{) = р₅ = 0,9 и р (В₂) = 1 — p_s — 0,1. Событие А при условии В равносильно безотказности системы, состоящей из двух последовательных двумя параллельными элементами каждая, для которой.

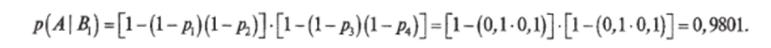
Событие А при условии В^ равносильно безотказности системы из двух заданных ветвей без учета элемента 5, для которой.

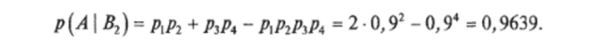
Подставляя полученные результаты в формулу (7.9) получаем.

Более обоснованное решение этой задачи см. в главе 9.

Теорема гипотез (формула Байеса^[1]). Следствием теоремы умножения и формулы полной вероятности является теорема гипотез, или формула Байеса. Пусть имеется полная группа несовместных событий (гипотез) Н_Х, Н₇,…, Н". Вероятности их до опыта известны и равны Р (Н_Х), Р (Н_г),…, Р (Н_п). Проведен опыт, в результате которого наблюдалось событие А. Требуется определить вероятности событий H_vH₂,…, H_n после опыта. На основании теоремы умножения и формулы полной вероятности имеем Пример. По данным ретроспективной статистической информации известно, что в группе электродвигателей каждый может иметь скрытые дефекты (повреждения) с вероятностью 0,01. Следовательно, для любого двигателя этой группы вероятность того, что он находится в исправном работоспособном состоянии определяется как Я (//,) = 0,99, а вероятность наличия скрытых повреждений —.

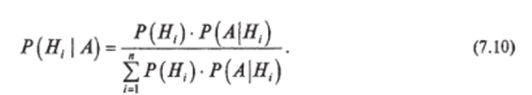
Р (Н₂) = 0,01.

Естественно, что несвоевременное устранение скрытых дефектов может привести к аварийному останову, ремонту и, как следствие, длительному простою основного технологического процесса. Для выявления скрытых повреждений используются методы и средства технической диагностики. В зависимости от сложности процедур диагностирования и применяемых при этом средств, получаемые результаты могут существенно отличаться.

Предположим, что существует некоторая конкретная методика и определены условия проведения работ по диагностике скрытых дефектов. При этом известно, что вероятность их безошибочного определения при условии, что обследуемый двигатель действительно их имеет — Р (А | Я₂) = 0,95. Тогда вероятность диагностирования скрытого повреждения при условии, что двигатель никаких дефектов не имеет — Р (А | Я,) = 0,05.

Таким образом, эта процедура диагностирования имеет пятипроцентную долю «ложных положительных результатов», и в среднем 5% из всех обследуемых электродвигателей, находящихся в работоспособном состоянии, будут ошибочно занесены в число не подлежащих дальнейшей эксплуатации. Аналогично, тест имеет пятипроцентную долю «ложных отрицательных результатов* и в среднем 5% из всех обследуемых двигателей со скрытыми дефектами будут признаны работоспособным и.

На этом основании возникает вопрос: «какова вероятность того, что на основании результатов теста, соответствующих принятию решения о невозможности дальнейшей эксплуатации двигателя, он действительно содержит скрытые дефекты?*.

Решение. По формуле (7.10) имеем:

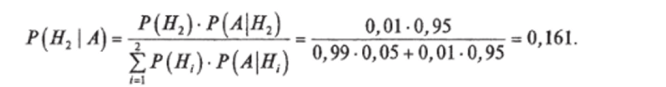
Таким образом, из всех обследуемых электродвигателей, тестирование которых дало результат, соответствующий наличию дефекта, только 16,1% будут действительно иметь такие дефекты.

Полученный результат говорит о том, что точность диагностирования дефектов электродвигателя на основании данной методики не вполне соответствует требуемой для принятия решений о возможности дальнейшей эксплуатации электродвигателя. Предположим, что доработка методики, диагностирование и применение для ее реализации новейших средств позволило изменить условные вероятности: Р (А | Я₂) = 0,995 и Р (А | Я,) = 0,005. Тогда.

Если предположить, что произошло уточнение ретроспективной статистической информации и реальные показатели надежности электродвигателей составляют Р (Н_Х) = 0,995 и Р (Н₂) = 0,005, то первоначальный диагностический тест (без доработки) дает результат.

Это говорит о том, что данная процедура тестирования в данных условиях практически непригодна для суждения о наличии скрытых повреждений.

Пример. Пропускная способность канала связи в системах телемеханики зависит от появления ошибки внутри канала (рис. 7.11). На вход могут подаваться два сигнала Х[ и *2• На выходе принимаются соответственно у и У2- 40% времени передается сигнал Х[ и 60% времени — сигнал Х2- Вероятность безошибочной передачи сигнала xj как у равна 0,75. Вероятность того, что входной сигнал х будет ошибочно принят как У2, равна 0,25. Аналогично, вероятность того, что сигнал, переданный как Х2, будет принят как У2 и у равна соответственно 0,9 и 0,1. При заданных условиях получен выходной сигнал у. Какова вероятность того, что исходный сигнал был xi?

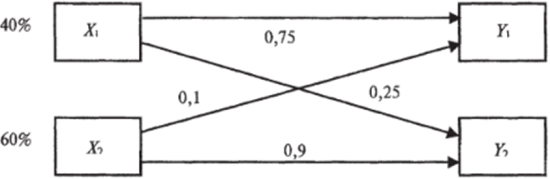
Рис. 7.11. Схема канала связи

Решение. Вероятности гипотез: Р(Я,) = 0,4; Р (Н₂) = 0,6. Условные вероятности события: «получен сигнал у» равны: Р (у_х |Я,) = 0,75; Р (у_х |Я₂) = 0,1.

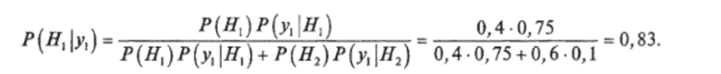
Пример. Пусть в условиях примера (рис. 7.9) произведено наблюдение технической системы и она оказалась в работоспособном состоянии, т. е. произошло событие А. При этом условии требуется определить вероятность того, что элемент 5 работал безотказно Р (В_Х | А) и отказал Р (В₂1 А).

Решение. Вычисления проводим по формуле (7.10):

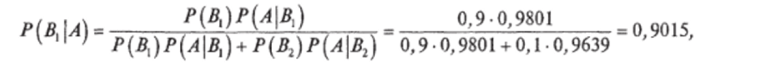
Таким образом, произошла некоторая переоценка гипотез: если априорная вероятность гипотезы В (безотказность элемента 5) составляла p (B_t) = 0,9, то апостериорная вероятность этой гипотезы (после наблюдения события А) стала р (В_]А) = 0,9015. Априорная вероятность гипотезы Bi (отказ элемента 5) составляла р (В₇) = 0,1, апостериорная вероятность её стала р (В₂ А) = 0,9 851.

Повторение испытаний. Формула Бернулли. Вероятность одного сложного события В, состоящего в том, что в п испытаниях событие А наступит с одной и той же р вероятностью к раз и не наступит п — к раз с вероятностью q = 1 — р по теореме умножения вероятностей независимых событий равна p^kqⁿ'^k. Таких событий может быть столько, сколько сочетаний из п элементов по к_у т. е. С*. Так как эти события несовместны, по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных событий. Поскольку вероятности этих событий одинаковы,.

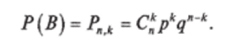
Пример. Вероятность нормального расхода электроэнергии потребителем в течение суток, равна 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит норму.

Решение, q — 1 — р = 1 — 0,75 = 0,25 — вероятность перерасхода.

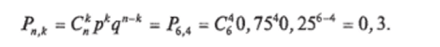
Если п велико, то искомая вероятность определяется приближенно в соответствии с локальной теоремой Лапласа (см. п*7.9).

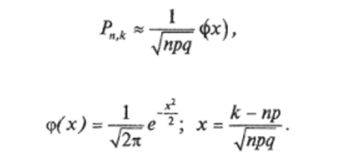
где Имеются таблицы [73 и др.],^[2] соответствующие положительным значениям аргумента этой функции. Поскольку функция <�р (х) четна,.

Пример. В сетевом районе 400 кабельных линий (КЛ). При испытаниях их повышенным напряжением вероятность пробоя в одном испытании 0,2. Найти вероятность того, что испытаний не выдержат 80 КЛ.

n п к — пр 80 — 400? 0,2 _{л Т)}

Решение. Вычислим: х = - =. =0. В соответствии с ука;

Jnpq >/400 0, 2 0,8.

занными выше таблицами получим: <�р (0) = 0,3989.

Тогда: _м " … • 0,3989 = 0,0498.

>00 0,2 0,8.

Вероятность того, что при достаточно большом п появится от кj до к2 интересующих нас событий вычисляется по приближенной формуле, которая носит название интегральная теорема Лапласа (см. п. 7.9):

• [1] Томас Байес (1702−1761) — английский математик и пресвитерианский священник, член Лондонского королевского общества, сформулировал и решил одну из основных задач, дающую возможность оценить вероятность событий эмпирическим путём, что играетважную роль в современной математической статистике и теории вероятностей.
• [2] Вентцелъ Е. С. Теория вероятностей. М.: Наука, 1969. 576 с.; Гмурман В. Е. Теория вероятностей и математическая статистика. М.: Высш. школа, 1977. 479 с.