Основы теории цифровой фильтрации

Под фильтрацией понимают любое преобразование информации (сигналов, результатов измерений и т. д.), при котором во входной последовательности обрабатываемых данных изменяют определенные соотношения (динамические или частотные) между различными компонентами этих данных. К операциям фильтрации относят дифференцирование, интегрирование, сглаживание, прогнозирование и разделение сигналов, а также фильтрацию, при которой осуществляются селекция (выделение) полезных составляющих сигнала и подавление мешающих его компонент и шумов (помех).

Цифровая фильтрация сигналов

Как и в аналоговых цепях, в зависимости от способа определения параметров фильтра — по импульсной характеристике или частотному коэффициенту передачи — возможны два подхода: временной и частотный. При временном подходе вычисляют дискретную свертку (6.24). Частотный подход основан на вычислении ДПФ (или БПФ) с последующим применением ОДПФ (или ОБПФ — обратного быстрого преобразования Фурье).

Цифровые фильтры обладают целым рядом преимуществ по сравнению с аналоговыми. Прежде всего это их стабильность и точность, а также возможность гибкой и оперативной перестройки структуры и параметров фильтров. Эти свойства цифровых фильтров в сочетании с возможностями схемотехнической микроэлектронной (а теперь и наноэлектронной) технологии обусловливают целесообразность их применения при обработке сигналов для решения различных прикладных задач.

Выбор типа и параметров фильтра определяется целями, поставленными при обработке сигналов. Обычно требования к цифровому фильтру формируются в процессе анализа исходных данных о спектральном составе полезного сигнала, мешающих сигналов и шумов. Цифровой фильтр должен обеспечить максимально возможное подавление спектральных составляющих помех при минимально допустимых искажениях полезного сигнала.

Цифровые фильтры имеют ряд принципиальных отличий от аналоговых. Основное отличие заключается в том, что в аналоговых фильтрах входной и выходной сигналы u (t) и y (t) являются непрерывными функциями времени, а в цифровых — дискретными последовательностями цифровых отсчетов сигналов Uj (t) = и_к, у₇(t) = у_к.

Проанализируем графики входных и выходных сигналов аналогового (рис. 6.15, а и б) и цифрового (рис. 6.15, в и г) фильтров (этот рисунок логически связан с рис. 4.26 и 4.27), которые позволяют наглядно представить отмеченную особенность цифровой фильтрации.

Ясно, что дискретность цифровых сигналов в принципе исключает возможность полного совпадения характеристик цифрового фильтра и его аналогового прототипа. При цифровой фильтрации непрерывный во времени аналоговый сигнал u (t) с помощью аналого-цифрового преобразователя заменяется последовательностью дискретных отсчетов u₇(t), взятых согласно теореме Котельникова через интервал дискретизации At.

Цифровая фильтрация заключается в цифровом преобразовании последовательности числовых отсчетов входного сигнала {u (kAt)} = {и^ в последовательность числовых отсчетов выходного сигнала {y (kAt)} = (у_А,}.

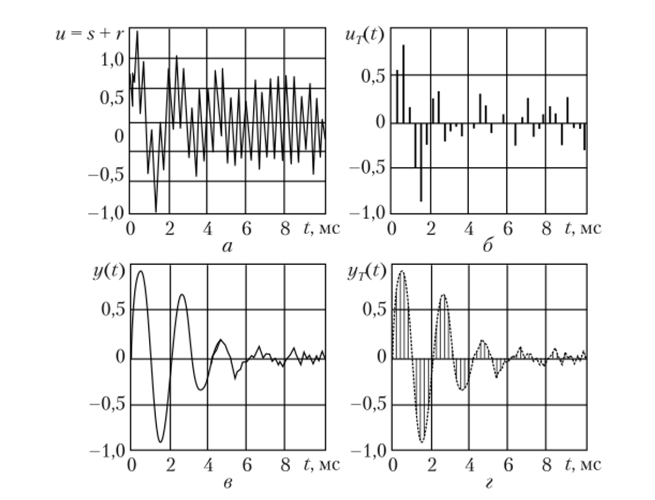
Рис. 6.15. К фильтрации сигналов:

а — исходный сигнал с шумом; б — сигнал на выходе аналогового фильтра; в — дискретизированный исходный сигнал с шумом; г — сигнал на выходе цифрового фильтра Рассмотрим упрощенную структурную схему цифровой обработки сигналов (рис. 6.16). Непрерывный сигнал u_BX(t) = и_вх (далее в схеме аргумент t опущен) поступает на вход АЦП, на выходе которого создастся двоичный цифровой код {u (k№)} = {щ) = и_т с фиксированным количеством разрядов, соответствующий дискретным отсчетам входного сигнала. Последовательность отсчетов {м₇}, закодированных определенными цифрами, поступает в цифровой фильтр (ЦФ), представляющий собой, по сути дела, сигнальный микропроцессор. В цифровом фильтре проводится цифровая обработка сигнала в соответствии с определенным алгоритмом, в результате чего на его выходе появляются новые цифровые коды {u_n(kAC)} = {м_ц} = и_ц, соответствующие профильтрованному входному сигналу.

Рис. 6.16. Упрощенная структурная схема цифровой обработки сигналов.

Обрабатываемый сигнал с цифрового фильтра поступает на ЦАП, в котором цифровая форма сигнала преобразуется в аналоговую м_а(?) = и_в. При включении ЦАП в схему обработки сигнала на ее выходе необходим синтезирующий фильтр (СФ) низкой частоты, который будет производить сглаживание аналогового сигнала. В результате сглаживания низкочастотным фильтром форма кривой выходного сигнала и_ВЬ1Х(?) = и_шх становится плавной. Кстати, использование входных и выходных сигналов в аналоговой форме (а значит, наличие АЦП и ЦАП) не всегда является необходимым. Так, при поступлении цифровых сигналов по линиям связи не нужен входной аналоговый сигнал, а ЦАП может отсутствовать, если конечный результат необходим только в цифровой форме.

Отметим важнейшее для цифровых фильтров обстоятельство, которое будет учтено далее: все основные положения теории линейных аналоговых фильтров, оперирующих с непрерывными сигналами, переносятся на математическую теорию цифровых фильтров, обрабатывающих дискретные и цифровые сигналы.