Распределение Вигнера на фазовом пространстве и отрицательная вероятность

Даже в нерелятивистской квантовой механике возникают отрицательные вероятности. Здесь нельзя ввести распределение вероятностей (Максвелла) координат х и моментов р, так же, как и в статистической механике. Это невозможно в силу соотношения неопределенности, которое препятствует одновременному измерению этих величин. Вигнер и Шилярд, тем не менее, нашли функцию распределения, которая впервые была применена для того, чтобы посчитать квантовую поправку к формуле давления газа. Если волновая функция ^(ац, …, х"), сокращенно ^>(х), задана, то соответствующая функция Вигнера определяется как.

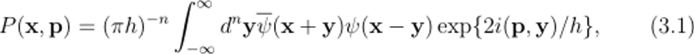
где х, у и р векторы, выражение (р, у) обозначает скалярное произведение. Дчя того, чтобы продемонстрировать фундаментальные свойства функции Вигнера, достаточно рассмотреть одну частицу на прямой. Таким образом, п = 1, а символы векторов с этого момента будут опускаться. Функция Вигнера проявляет замечательные сходства с распределением вероятностей. Она даст правильные вероятности для координат при интегрировании её по переменной р

и наоборот, даст правильные вероятности для моментов при интегрировании, но переменной х,.

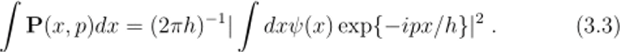
Хотя Вигнер называл её вероятностной функцией для координат и моментов (в новейших работах используется понятие ‘квази-вероятности'), он подчёркивал в том же контексте, что она не может действительно интерпретироваться таким образом «как явствует из того факта, что она принимает отрицательные значения. Однако, это нс должно мешать сё использованию в вычислениях в качестве вспомогательной функции, которая подчиняется многочисленным соотношениям, каковые мы и могли бы ожидать от такой вероятности» [1111. Существование функций Вигнера, принимающих отрицательные значения, строго доказывается при условии двух очень общих ограничений на распределения Р, которые, можно сказать, определяют этот вид распределений вероятностей, а. именно:

(i) Р(х, р) должно быть эрмитовой формой от вектора состояния ?ф (х), т. е., если М (х, р) самосопряженный оператор, то верно равенство.

Э го условие делает величину Р (.т, р) действительным числом.

(ii) Р (.г, р) — должно давать правильные средние значения для всех операторов, которые являются суммами функций от р и функций от х,.

Это условие — в некоторой степени ослабленная форма равенств (3.2) и.

(3.3), которые, строго говоря, должны пониматься как аксиомы функции Вигнера и должны быть удовлетворены в любом случае. Далее, достаточно рассмотреть такие 0, которые являются линейными комбинациями 0 = аф + Ьф2 произвольных фиксированных функций, исчезающих на определенных интервалах по переменной х. Теперь, потребовав выполнения соотношения.

для всех х и р и для каждого такого 0, Вигнер получает противоречие, которое вкратце звучит так:

Рассмотрим интервал /, внутри которого функция 0(.т) = 0 и д (х) > О, в то время как д (х) = 0 вне интервала, а f (p) = 0 везде. Тогда равенство (3.5) приводит к формуле.

Следовательно, равенство.

для всех р (за исключением множества меры нуль).

Из соотношения (3.6) и условия наложенного на д (х) получаем (лемму Вигнера): Если функция 'ф (х) исчезает на интервале /, то соответствующая функция Р (.г, р) исчезает (за исключением множества меры пуль) при всех значениях переменной х в этом интервале. Теперь, рассмотрим две функции ф (х) и ф2(х), которые исчезают вне двух ненересекающихся интервалов 1 и /₂, соответственно. Вследствие формулы (3.4), функция Р (х, р), соответствующая разложению ф = аф + Ьф₂, будет иметь вид.

Полагая Ь = 0, очевидно, что Pi, является функцией Вигнера состояния (а Р'2 — функцией Вигнера состояния ф₂). Смысл величин Р₁₂ и P_2i не столь очевиден, по нам нет нужды беспокоиться об этом, поскольку обе они тождественные нули. Это можно увидеть, рассматривая любой интервал /' в дополнении к /]. Так как, согласно вышеназванной лемме, функция Р. исчезает почти везде на интервале величина (3.9) не может быть положительной при произвольном выборе констант а и Ь если не будет выполнено равенство Pj₂ = P_>i = 0 вне интервала 1. Точно такое же доказательство применим к интервалу /₂. Таким образом, вместо разложения (3.9) почти всюду будем иметь равенство.

Для того, чтобы завершить противоречие, давайте обозначим преобразования Фурье функций ф и ф₂ через ф{р) и 0₂(р), соответственно. Тогда уравнение (3.3) запишется так:

Так как оно должно быть верно для всех а и Ь. то мы должны получить тождественно, но р равенство ф (уфф₂(р) = б. Однако это невозможно, поскольку функции ф и ф₂, будучи преобразованиями Фурье от функций, ограниченных на конечных интервалах, являются аналитическими функциями от своих аргументов и не могут равняться нулю на любом конечном интервале.

Для того, чтобы проиллюстрировать этот результат, формализм функции Вигнера может быть применён к парадигме квантовой теории — линейному гармоноческому осциллятору (см. В. Мукенхайм [90|). Из его гамельтониана.

и уравнения для нахождения собственных значений этого гамильтониана: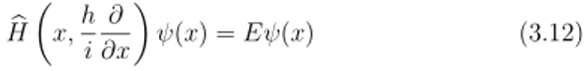

легко найти волновую функцию основного состояния.

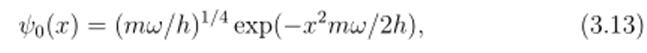
соосггветсвую11 jcro энергии Во = hid/2. Подстановка (3.13) в (3.1) и интегрирование по переменной у приводит к формуле.

которая не проявляет никакой аномалии, так как она является неотрицательной, а затем, проинтегрированная по х, даёт правильное распределение импульса.

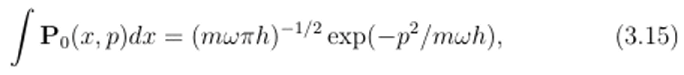
которое является распределением Гаусса с нулевым математическим ожиданием и среднеквадратичным отклонением (Ар)² = тык/2. Интегрирование по переменной р даёт, как и ожидалось, квадрат от величины в формуле (3.13),.

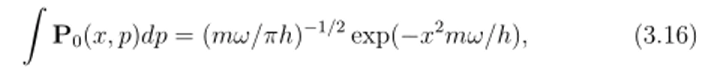
которая также есть распределение Гаусса с нулевым математическим ожиданием и среднеквадратичным отклонением (Ат)² = к/2ти>. Распределения Гаусса удовлетворяют соотношению неопределенности Гейзенберга в его предельной форме, т. е. как равенство. Из формул (3.15) и (3.16) получаем, что (Ат) (Ар)² = к/2. Можно было бы также заметить, что распределения момента и позиции статистически независимы, потому что J Pqdp J P₀dx = Ро То есть, коэффициент ковариации равен нулю. Ясно, что этот пример не противоречит вигнсровскому ‘доказательству отрицательности', поскольку последнее говорит только о том, что существуют функции состояний для которых соответствующие распределения вероятностей Р (д;, р) не могут быть везде неотрицательными. Одним из них является первое возбуждённое состояние гармоноческого осциллятора. Используя функцию состояния первого возбуждённого уровня, тот же описанный выше формализм приведёт к соответствующей функции Вигнера.

Если Н — гамельтониан (3.11) и Ь_п — n-ый полином Лагерра, то функция Вигнера, соответствующая то-ому возбуждённому состоянию может выражаться как.

или, используя формулу (3.14), получим.

Поскольку Р₀ — везде неотрицательно, нам следует проверить выражение.

Полином Лагерра первой степени имеет вид:

Следовательно, Р (х, р) будет отрицательным для гамильтониана.

Таким образом, распределение Вигнера Pi («T, p) становится отрицательным только в очень маленькой области (эллипс (3.21)). Так как энергия первого возбуждённого состояния Е = 11пи, то вероятность размеров энергии Р(Е < iiLo/A) (где Е — энергия квантового гармоноческого осциллятора) равна нулю. Значит, в этом примере отрицательные значения распределения Вигнера Р (х, р) соответствуют событиям, которые имеют нулевую обычную вероятность. Использование распределение Вигнера может быть интерпретировано как вид расщепления нулевой обычной вероятности с помощью использования отрицательных чисел (как класс меток для обозначения вероятностей событий, которые отождествляются в рамках обычной теории с меткой ‘О').

Теперь рассмотрим функцию Вигнера второго возбуждённого состояния. Полином Лагерра второй степени:

Используя равенство (3.19), получим, что Р₂(.т, р) становится отрицательным при.

Поскольку энергия второго возбуждённого состояния Е₂ = §hcj, то вероятность размеров энергии Р(Е < |/?.cj (1 -1- 2^-1^²)) равна нулю. Значит, в этом примере отрицательные значения распределения Вигнера Р](т, р) также могут интерпретироваться как дополнительные метки для вероятностей (которые отождествляются с меткой ‘0^: в обычной теории вероятностей). соответствующих событиям, которые имеют нулевую обычную вероятность. При Н = 0 и Я —> оо, тем не менее, значение Р-2(т, р) неотрицательно.

Мы отметим некоторые общие черты функций Вигнера для линейного гармонического осциллятора. Из предельного равенства lim^-too L_n(u) = (—l)ⁿwⁿ и равенства (3.17) находим, что распределение Р" является положительным и ассимптотически стремящимся к нулю при Я стремящемся к бесконечности. Частный случай, когда Я = 0, L_n(0) = п! вместе с формулой (3.17) даёт нам то, что функция Р" с чётной степенью положительна, а функция Р" с нечётной степенью — отрицательна при Я = 0.

Наиболее интересным в представленном контексте является то, что все эти функции Вигнера ненулевой степени неизбежно будут давать как положительные, так и отрицательные значения. Это легко можно увидеть из соотношения ортогональности.

Коэн (подробнее, см., например, обзорную статью [90)) смог показать, что широкий класс функций распределений вероятностей подаётся довольно общим выражением.

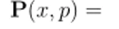
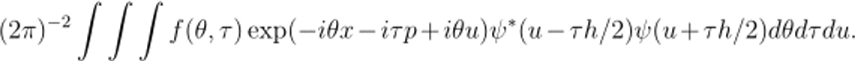
Здесь / просто функция вязкости. Полагая / = 1. заменяя т на —2у/к и интегрируя по переменным в и и, мы получим первоначальную функцию Вигнера (3.1). Другие функции распределения могут быть построены при различных функциях /, если только / удовлетворяет условию /(О, т) = /(0,0) = 1j чтобы дать правильное квантово-механическое предел ы I ое рас 11 редела ню.

Коэн налагал следующие условия на общую функцию распределения Р(х, р): (i) равенства (3.2) и (3.3); (ii) если квантово-механическое среднее значение оператора Эрмита М равно (Л/), тогда должна существовать функция ум (х.р) такая, что.

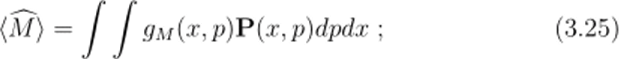
и, для любой функции К верно равенство.

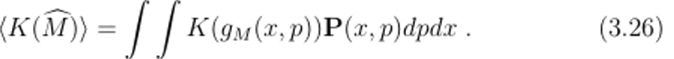
Было показано, что, независимо от того является ли Р положительно нолуопрсдслснной или нет, условие (ii) никогда не удовлетворяется. Функция Вигнера Р. для гармонического осциллятора, например, даёт правильное значение для средней энергии, но не даёт нулевое среднеквадратичное отклонение, которое следует ожидать для квантово-механической энергии собственного состояния. Он заключает: «Безусловно, могут приводится аргументы, что классический формализм может использоваться до тех по]) пока мы не требуем, чтобы функция, которая должна использоваться для получения среднего значения функции К от д, совпадала с К (д). Но это уведёт нас ещё дальше от концептуальной основы классической теории вероятностей, чем сама квантовая механика!». Таким образом, классическая физика или классическая вероятность!

В завершение, отметим, что равенство (3.25) есть прямое следствие формулы полной вероятности. Пусть М — ортогональный проектор в гильбертовом пространстве квантовых состояний. Он представляет физическую наблюдаемую М = 0,1. Здесь Р (М = 1) = (М) и равенство (3.25) не что иное как формула полной вероятности для первоначального распределения вероятностей Р (.т, р) и условных вероятностей.

P (M = 1 /(x.p)) = дм (х, р). Если мы следуем нашей интерпретации отрицательных вероятностей, тогда мы получим, что эрмитовы операторы представляют все физические наблюдаемые, которые позволяют делать измерения, обладающие свойством статистической стабилизации. Здесь мы могли бы получить (дтя некоторых состояний) отрицательное среднее значение для наблюдаемой с положительными значениями.

На основе нашей интерпретации отрицательных вероятностей мы можем завершить этот раздел следующим заключением.

Заключение

С частотной точки зрения отрицательные значения распределения вероятностей Вигнера — это проявление отсутствия статистической стабилизации относительных частот и^((х, р) € U) для некоторых областей U фазового пространства; с точки зрения теории ансамблей отрицательные значения распределения вероятностей Вигнера — это проявление нерегулярной структуры бесконечных статистических ансамблей.