Плотность тока. 
Прикладная физика. 
Механика. 
Электромагнетизм

Электромагнитное поле, создаваемое зарядами, зависит не только от их положения, но и от скорости. Поэтому нам понадобится еще одна величина.

Пусть, как описано выше, пространство разбито на ячейки ЬУ_Г Если в ячейку попали заряженные частицы с зарядами q_k и скоростями v_A, вычислим величину.

где сумма берется по всем частицам, попавшим в /'-ю ячейку. Таким образом, каждой ячейке ставится в соответствие вектор у, который меняется, вообще говоря, от ячейки к ячейке. В пределе вектор j является функцией точки (в окрестности которой строится ячейка):

Определенный таким образом вектор называется плотностью тока. Смысл этой величины выясним чуть позже.

Итак, источник электромагнитного поля описывается скалярной функцией р (г) и векторной функцией Дг).

Поток вектора

Чтобы сформулировать уравнения поля, нам нужны еще некоторые математические конструкции.

Пусть имеется векторное поле.

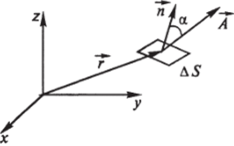
Рис. 6.2.

A (x, y, z) — Это значит, что в каждой точке пространства (х, у, z) задан вектор А, причем векторы А ведут себя достаточно хорошо (скажем, не меняются хаотично отточки к точке). Смысл вектора А нас сейчас не интересует. Рассмотрим некоторую точку г. В этой точке вектор А имеет определенное значение А (р) (рис. 6.2). В окрестности точки г построим малую площадку площадью AS, содержащую точку г. Ориентация этой площадки определяется единичным вектором Я, |й| = 1. Вычислим величину.

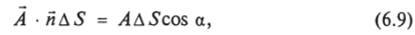
где А? Я = А_п — /Icosa — скалярное произведение векторов Лий.

Эта величина называется потоком вектора А через площадку AS * Рассмотрим теперь некоторую поверхность S (рис. 6.3). Разобьем поверхность на малые площадки. Пусть AS. — площадь /-й площадки, Я, — ее нормаль, А. — значение вектора А в некоторой точке.

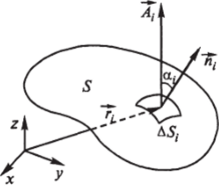
Рис. 6.3.

г, внутри площадки (напомним, А задан в каждой точке пространства, так что мы можем определить его и в этой точке).

Вычислим величину А, • Я. Д5, для /-й площадки и далее вычислим сумму У' А, ? Я, AS, по всем площадкам, составля;

ющим нашу поверхность S (отметим, что значения А, и Я, меняются, вообще говоря, от площадки к площадке, так что вычисление такой суммы при достаточно мелком разбиении AS. технически непростая задача). Предел этой суммы при AS. —> 0 называется потоком вектора А через поверхность S:

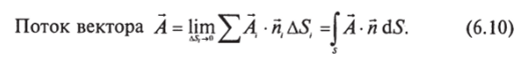
Правая часть (6.10) есть обозначение этого предела и определение так называемого поверхностного интеграла. В анализе изучаются способы вычисления таких интегралов при достаточно хороших функциях Л (г) и поверхностях 5. Обычно произведение iidS объединяется в один вектор d5 = «d5, т. е. ориентированная площадка рассматривается как вектор.

Смысл введенной конструкции можно пояснить таким примером. Рассмотрим течение воды в реке. В каждой точке пространства внутри потока определим скорость воды. Получим векторное поле v®. Рассмотрим поверхность внутри потока, образованную, например, рыболовной сетью. Ячейки сети, кстати, могут задавать разбиение поверхности S на элементы ДS_r Определим скорость v. внутри каждой ячейки и вычислим сумму.

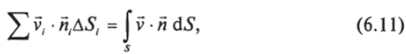
т. е. поток вектора v через поверхность S, образованную сетью. Эта сумма будет представлять объем воды, протекающей через поверхность сети за секунду. Если сеть ставить разными способами, будем получать разные потоки. В частности, ее можно поставить так, что поток будет равен нулю.