Атомная орбиталь. 
Квантовые числа. 
Формы орбиталей

После завершения формального описания квантово-механического движения стало ясно, что в атомном пространстве каждый объект имеет такую характеристику, как атомная орбиталь.

Атомная орбиталь (АО) — область пространства вокруг ядра атома, в которой по законам квантовой механики с наибольшей вероятностью находится электрон с заданной энергией.

Энергетическое состояние электрона описывается функцией трех целочисленных параметров п_} I, т_1У которые называются квантовыми числами. При определенных значениях квантовых чисел можно получить характеристики области, где может находиться электрон.

Квантовые числа имеют следующий физический смысл:

• • п — главное квантовое число, характеризует энергетический уровень и размер орбитали;
• • / — орбитальное квантовое число, характеризует энергетический подуровень и форму орбитали;
• • т_{ — магнитное квантовое число, учитывает влияние внешнего магнитного поля на энергетическое состояние электрона.

Главное квантовое число п является натуральным и соответствует номерам периодов в таблице Д. И. Менделеева (1, 2, 3, 4, 5, 6, 7). Главное квантовое число определяет основную долю энергии электрона, находящегося на данной орбитали. Это квантовое число называют также номером энергетического уровня. Чем больше п, тем больше размер орбитали.

Атомы, в которых электроны находятся на орбиталях с большим значением п (п > 8), называются ридберговскими атомами. Первые экспериментальные данные по ридберговским атомам в радиоастрономии были получены в 1964 г. сотрудниками ФИАПа (Р. С. Сороченко и др.) на 22-метровом зеркальном радиотелескопе. При ориентации телескопа на туманность Омега в спектре ее радиоизлучения была обнаружена линия излучения с длиной волны X = 3,4 см. Эта длина волны соответствует переходу между ридберговскими состояниями п = 90 и п = 91 в спектре атома водорода. Сегодня в лаборатории получены ридберговские атомы с п ~ 600! Это почти макроскопические объекты размером около 0,1 мм и временем жизни ~1 с. Изучение ридберговских состояний атомов оказалось полезным в работах по созданию квантовых компьютеров.

При этом увеличение размера не меняет формы орбитали. Чем больше п_у тем больше энергия электрона. Электроны с одинаковым значением главного квантового числа находятся на одном энергетическом уровне. Номер п энергетического уровня указывает на число подуровней, входящих в состав данного уровня.

Орбитальное квантовое число I может принимать значения / = 0, 1,2,… до (п — 1), т. е. при данном главном квантовом числе п орбитальное квантовое число / может принять п значений. Орбитальное квантовое число определяет геометрическую форму орбиталей и определяет орбитальный момент количества движения (импульс) электрона, т. е. вклад данного подуровня в общую энергию электрона. Кроме численных значений, орбитальное квантовое число / имеет и буквенное обозначение:

Формы 5-, р-, (1-, /-орбиталей приведены на рис. 1.1. Знаки, проставленные на геометрических элементах орбиталей, не являются знаками заряда, а относятся к значениям волновой функции у для этих элементов. Поскольку при расчете вероятности рассматривается | н/|²— квадрат величины по модулю, то области орбиталей волновой функции у со знаками «+» и «-» становятся равнозначными.

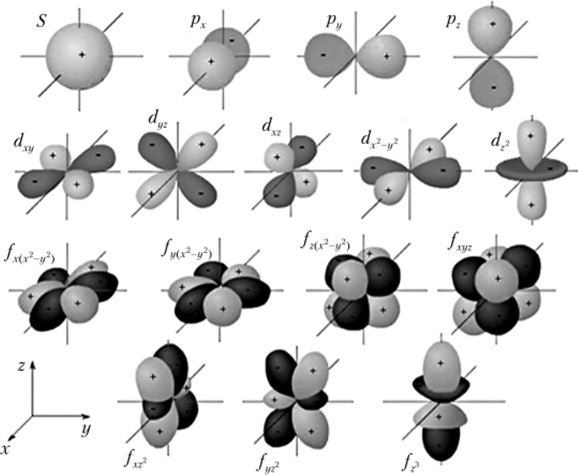
Рис. 1.1. Формы орбиталей.

Сложная форма большинства орбиталей обусловлена тем, что волновая функция электрона в полярных координатах имеет две составляющие — радиальную и угловую. При этом вероятность нахождения электрона в данной точке зависит как от ее расстояния до ядра, так и от направления в пространстве вектора, связывающего ядро с этой точкой. Эти функции зависят как от / (для 5- и р-орбиталей), так и от т₁(для с1— и /-орбиталей).

Например, абрисом (внешним контуром) всех 5-орбиталей является сфера. По оказывается, что вероятность обнаружения электрона внутри этой сферы не равномерна, а напрямую зависит от расстояния данной орбитали от ядра. На рис. 1.2 показана внутренняя структура 15- и 25-орбиталей. Как следует из рисунка, 25-орбиталь подобна «двухслойной луковице» с внутренними оболочками, расположенными на расстоянии 1 и 4 радиуса боровской орбиты. Как правило, в химии факт сложности внутреннего строения орбиталей не играет значительной роли и в данном курсе нс рассматривается.

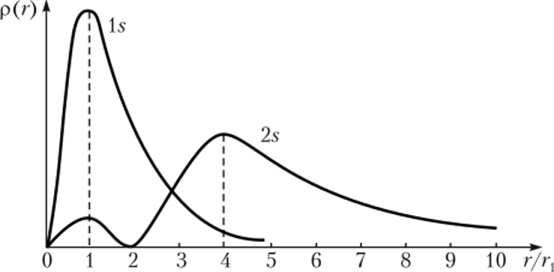
Рис. 1.2. Распределение вероятности обнаружения электрона в атоме водорода в состояниях is и 2s. г_{ = 5,29*10 ¹¹ м — радиус первой боровской орбиты.

Источник: wvw.college.ru/enportal/physics/content/chapter9/section/paragraph3/theory.html.

Орбитальное магнитное квантовое число m_t может принимать значения от -/ до +/, включая нуль. Это квантовое число определяет ориентацию орбитали в пространстве при воздействии внешнего магнитного поля и характеризует изменение энергии электрона, находящегося на этой орбитали, под влиянием внешнего магнитного поля. Количество орбиталей с данным значением т₁ составляет (2/ + 1).

Рассмотренные три квантовых числа п, /, т_{ являются следствием решения волнового уравнения Шредингера и позволяют определить энергию электрона через описание его волновых свойств. При этом не учитывался двойственный характер природы элементарных частиц, их корпускулярноволновой дуализм в описании энергетического состояния электрона.

Собственное магнитное квантовое число электрона m_s {спин). Как следствие корпускулярных свойств электрона, в описании его энергетического состояния играет роль еще одно число — собственное квантовое число m_s электрона {спин). Это квантовое число характеризует не орбиталь, а свойство самого электрона, находящегося на этой орбитали.

Спин (от англ, spin — вертеть[-ся], вращение) — собственный момент импульса элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого. Часто используемая аналогия для описания спина как свойства, связанного с вращением электрона вокруг своей оси, оказалась несостоятельной. Такое описание приводит к противоречию со специальной теорией относительности — экваториальная скорость вращения электрона в этой модели превышает скорость света.

Введение

спина явилось удачным применением новой физической идеи: постулируется, что существует пространство состояний, никак не связанных с перемещением частицы в обычном пространстве. Необходимость введения такого пространства состояний свидетельствует о необходимости рассмотрения и более общего вопроса о реальности физического многомирия.

Электрон проявляет свои собственные магнитные свойства в том, что во внешнем электрическом иоле собственный момент импульса электрона ориентируется либо по полю, либо против ноля. В первом случае принимается, что собственное квантовое число электрона m_s = +½, а во втором m_s = -½. Отметим, что спин — единственное дробное число среди набора квантовых характеристик, определяющих состояние электрона в атоме.