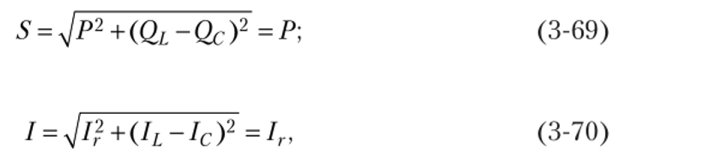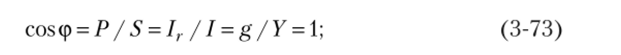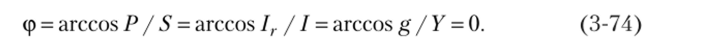Резонанс токов и частотные характеристики

Резонанс токов имеет место в цепях вида рис. 3.14, а, которые называются параллельными колебательными контурами, поскольку в них источники питания и ветви с г, L и С параллельны. Исходя из условия наступления резонанса, рассмотрим соотношения между электрическими величинами и параметрами цепи по рис. 3.14, а.

1. Разделив (3.52) на напряжение U_y получим.

т.е. при резонансе токов реактивные токи индуктивности и емкости равны между собой (рис. 3.14, б). Отсюда и название — резонанс токов.

2. Разделив (3−52) на U² или (3−67) на U, будем иметь.

Рис. 3.14.

Из соотношений (3−68) очевидно, что при резонансе токов реактивные проводимости, индуктивности и емкости равны между собой. Кроме того, очевидны возможные пути получения резонанса токов. Они те же, что и при резонансе напряжений, т. е.: а) изменением частоты/источника питания при постоянствах L и С; б) изменением индуктивности L контура при постоянствах / и С; в) изменением емкости С контура при постоянствах /и L.

• 3. При резонансе токов:
  • • полная мощность цепи

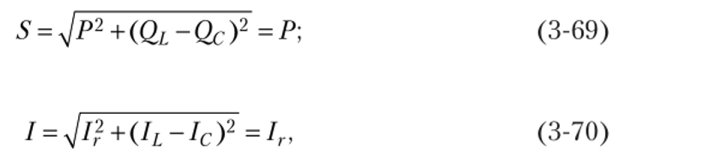
• полный ток что отражено на векторной диаграмме, изображенной на рис. 3.14, б

• полная проводимость.

• • полное напряжение
• • коэффициент мощности

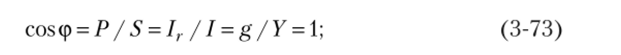
• угол сдвига по фазе между напряжением и током.

Анализ полученных выражений показывает, что при резонансе токов полные мощность, ток, проводимость и напряжение в цепи равны их активным составляющим, вследствие чего cos (p = 1, ср = 0.

Кроме того, при b_L = b_c «g

т.е. полный ток в цепи / минимален, a I_L = 1_с может значительно превосходить 1.

Заметим, что при резонансе токов обмен реактивной энергией между L и С происходит, минуя источник питания, поскольку ветви с L и С соединены параллельно. При этом, если бы г = или g = 0, т. е. ветвь с г в цепи отсутствовала бы, то свободные колебания энергии между L и С (переход магнитной энергии в электрическую и обратно) продолжались бы бесконечно долго. Поскольку же реально в любой цепи г присутствует, то колебания затухают. Чтобы колебания продолжались, нужно, чтобы источник подбавлял в цепь энергию, расходуемую на г, с частотой / = /_р.

Частотные характеристики цепи по рис. 3.14, а представлены на рис. 3.14, в. Обосновать их ход предлагается читателям.