Завершающие процедуры расчета процесса ректификации по двухконтурному методу

а) Процедура инициализации (задание начальных значений)

Шаги по пунктам 1−4 проводят подобно общей процедуре инициализации (см. раздел 3.12).

• 5) Рассчёт параметров простой термодинамической модели Ар B_Jt ац, bjj, Cjy Dp Ep Fp Kbjy (Zjj по точной модели, используя прогнозные значения от пункта 1 до пункта 4.
• 6) Расчет по уравнениям (3.13) и (3.53) начальных значений Rj, Rj

и S_bj.

• б) Расчёт на внутреннем итерационном контуре
• 7) Расчёт покомпонентного жидкостного потока Uj путём решения системы N линейных уравнений (3.54) для каждого /-го компонента, записанной в виде матрицы:

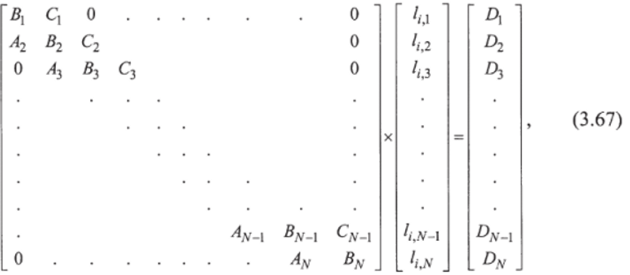
где.

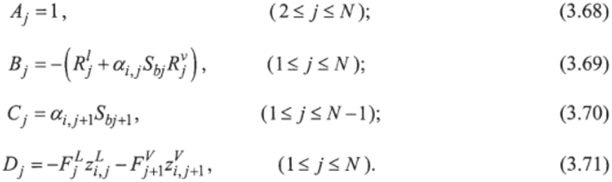
Система (3.67) решается методом Томаса (Приложение А).

• 8) Расчёт по уравнению (3.55) парового покомпонентного потока Vy.
• 9) Расчёт по уравнениям (3.14) общего потока жилкой Lj и паровой Vj фаз.
• 10) Расчёты профиля состава жидкой фазы Хц ведётся по уравне-

с нию (3.14), a Kbj — по уравнению ?^i, j^xi, j ⁼ 1 • С учетом уравнения.

/=1.

(3.52), имеем:

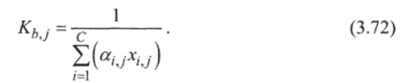
Вычисляется температура на у-й тарелке по новому значению Ktj из уравнения (3.58):

По этой точке получаем переменные параметры /у, Vy и 7)-, удовлетворяющие уравнениям покомпонентного материального баланса и фазового равновесия (для прогнозных термодинамических свойств). Однако эти величины нс удовлетворяют уравнениям теплового баланса (и их альтернативным уравнениям). Поэтому необходимо решить систему уравнений теплового баланса методом Ньютона-Рафсона (пункты 11−18).

11) В качестве внутренних итерационных переменных выбирается величина In(SbJ), определяющаяся наряду с другими итерационными переменными по формуле:

Для простой колонны, если подвод и отвод тепла известны, то не нужно никаких других итерационных переменных. Для каждого бокового отбора (боково-отборный фактор) выбирается один из дополнительных внутренних итерационных переменных In(U/Lj) или In(W/Vj).

• 12) Расчёт по формулам (3.65), (3.66) энтальпии всех потоков.
• 13) Расчёт нормы вектора функции Hj (3.56):

• 14) Расчёт по внутренним итерационным переменным элементов матрицы Якоби вектора функций Hj (3.56).
• 15) Расчет по методу Ньютона-Рафсона [35] коррекции внутренних итерационных переменных.
• 16) Расчёт по формуле (3.47) нового значения внутренних итерационных переменных.

17) Проверка нормы вектора функции (3.75): где с= КГ¹⁰

Если условие (3.76) удовлетворяется, то расчёт переходит от внутреннего к внешнему итерационному контуру, в противном случае расчёт повторяется с 13 до 16 пункта (можно использовать метод Бройдена или метод Ньютона-Рафсона).

• 18) Перед тем как условия с пункта 13 до 17 выполнятся, используются пункты с 7 до 10 для расчёта новых значений начальных переменных ^хф Уф 1ф v/j, Lj, Vj и Tj. Эти новые значения переменных используются на внешнем итерационном контуре для того, чтобы простая термодинамическая модель соответствовала более точной термодинамической модели.
• в) Расчет на внешнем итерационном контуре
• 19) Используя начальные значения переменных по пункту 18, рассчитываются относительная летучесть и энтальпия фаз по точной термодинамической модели. Если они хорошо согласуются с предыдущими значениями, примененными для инициализации переменных на внутреннем итерационном контуре, то оба контура сходятся. В противном случае расчёт переходит к пункту 20 и заканчивается при выполнении условия:

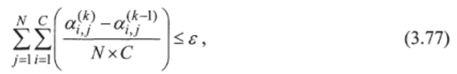
где е — 10.

• 20) Расчёт параметров с пункта 5.
• 21) Расчёт значений Sbj, Rj, R.) (пункт 6).
• 22) Повторяется процедура расчёта на внутреннем итерационном контуре от пункта 7 до пункта 18.

Двухконтурный метод не всегда обеспечивает сходимость системы уравнений. Однако в большинстве случаев этот метод обладает быстродействием и надёжностью. При недостаточно хорошем начальном приближении переменных двухконгурный алгоритм трудно сходится (поток фаз может быть отрицательным или с нулевым результатом в некоторых точках колонны). Для преодоления этой трудности все стриппингфакторы умножают на множитель St, т. е.

Первоначальное значение Sb выбирается таким образом, чтобы процедура инициализации создала целесообразное распределение потоков фаз. Значение Sb можно рассчитывать только один раз или по каждому новому значению Sbj.

Блок-схема алгоритма расчёта процесса многокомпонентной ректификации по двухконтурному методу приведена на рис. 3.12.

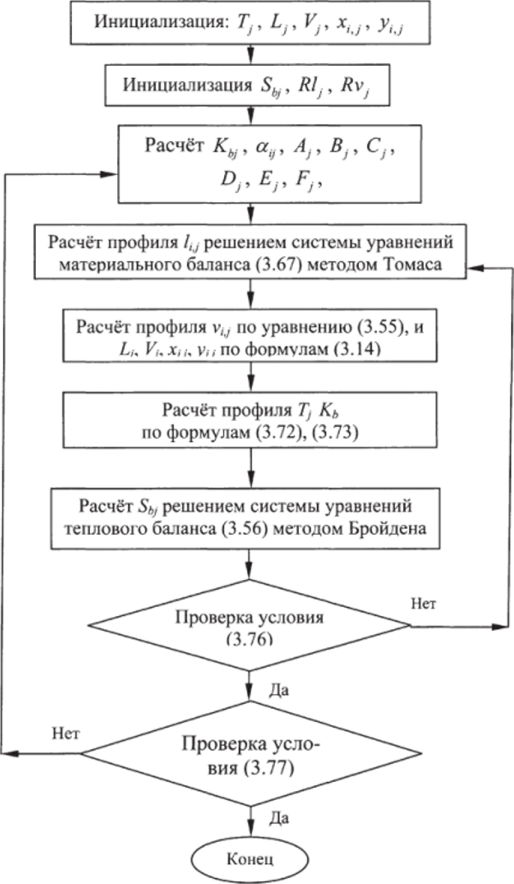
Рис. 3.12. Блок-схема алгоритма расчёта процесса ректификации по двухконтурному методу.