Равновесная форма. 
Кристаллография: зарождение, рост и морфология кристаллов

С понятием об идеальной огранке непосредственно связано представление о равновесной форме кристалла, что особенно актуально для микроразмерных твердых фаз, когда поверхностная энергия сопоставима с объемной составляющей. Согласно Гиббсу, предложившему ее определение в 1878 г., среди всех кристаллических форм равного объема, следовательно, постоянной массы и равной объемной энергии, равновесной является та из них, которая обладает наименьшей свободной поверхностной энергией. Спустя семь лет П. Кюри независимо дал близкую формулировку: кристалл, находящийся в равновесии с раствором или расплавом, принимает огранку с наименьшей поверхностной энергией.

Условие Гиббса выражается соотношением.

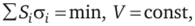
где Sj и Of — площадь и удельная свободная энергия i-й грани, а V — объем кристалла. Одно из наглядных решений этого вариационного уравнения было проиллюстрировано Г. Вульфом в 1901 г. Оно известно также как теорема Вульфа: минимум поверхностной энергии для данного объема многогранника достигается при таком взаимном расположении его граней, когда они удалены от одной и той же точки внутри его на расстояние, пропорциональное их капиллярным постоянным (другими словами — удельной поверхностной энергии), т. е. 0]: о₂: ст₃: … = h, :h₂:h₃: … .

Для ее доказательства можно использовать решение Я. И. Френкеля и двумерное изображение (сечение) кристалла, показанное на рис. 2.38, где h₍ — длины нормалей, выходящих их точки внутри кристалла к каждой его грани, a S, — площади граней.

Рис. 2.38. Сечение многогранника Вульфа:

S, — проекции граней; h, — расстояние грани от центра кристалла Поверхностная энергия такого многогранника.

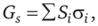
а его объем.

Если S, и hj меняются на бесконечно малые величины dS, и d/t" то полный дифференциал объема.

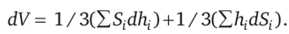
С другой стороны, с точностью до бесконечно малых величин первого порядка его изменение будет иметь вид.

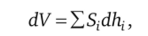
поскольку Sjdh, — бесконечно малый объем, описываемый гранью при ее перемещении на расстояние dh_t. По формальным соображениям два последних уравнения приравниваются друг к другу, откуда следует, что.

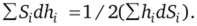
На основании этого приема изменение объема допустимо записать в следующем виде:

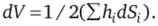
Поскольку при V = const G_s = min, то.

и.

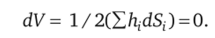
Эти два уравнения могут сосуществовать лишь при условии, когда Oi: а₂: а₃; … = h₁: h₂: h₃: …, т. е. <�т, / d, = const. Это доказательство справедливо для мелких кристаллов и при пренебрежимо малом вкладе избыточной энергии ребер по сравнению с поверхностной энергией граней.

Если известна зависимость поверхностной энергии от кристаллографического направления, то можно построить такой многогранник. Для этого из условной центральной точки проводят радиус-векторы, перпендикулярные к возможным граням. Затем на расстояниях, пропорциональных удельной поверхностной энергии, изображают искомые грани, отвечающие равновесной форме кристалла.

Один из способов получения констант а, / /г, базируется на анализе уравнения Томсона — Гиббса (см. вывод уравнения в п. 2.2.1.

и рис. 2.11), согласно которому давление насыщенного пара над поверхностью раздела между паром и жидкостью зависит от ее кривизны, или другими словами — от радиуса ограничиваемой ею новой фазы:

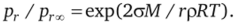
Из него видно, что, чем круче поверхность, тем больше относительная разница давлений пара. Возрастает она также при увеличении о. Как и для капли жидкости, равновесное давление пара мелкого кристалла растет с уменьшением его размеров и, по аналогии, можно с некоторой степенью условности перенести подобные рассуждения на системы «пар — кристалл» и «жидкость — кристалл».

В общем случае несферической поверхности раздела при фазовом равновесии вещество будет «перекачиваться» от участков с большей кривизной к уплощенным.

Для расчета констант о_; / ft, исходят из модифицированного уравнения Томсона — Гиббса:

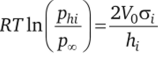
Переходя к химическим потенциалам кристаллов, равновесных с паром,.

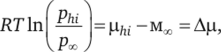
его можно переписать в виде.

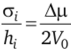
Поэтому определенному химическому потенциалу соответствуют кристаллы с фиксированным расстоянием ft, граней от центральной точки. Если оно больше того, что отвечает условию минимальности, кристаллы будут расти, а в противном случае — испаряться.

Разность химических потенциалов ц_;" - ц" характеризует изменение свободной энергии при переходе одного моля вещества из маленького кристалла в кристалл бесконечных размеров. Повышение давления пара в формуле Томсона — Гиббса как функция размера кристаллического зародыша реализуется лишь для мелких кластеров. Для кристаллов же порядка первых сантиметров оно имеет величину порядка 10^_6—10~⁸ и, например, при а, = 10^-7 Дж/см², ft, = 1 см, V₀ = 25 см³, Т = 300 К, R = = 8,31-Дж/град-моль Ар/р^ составит 2T0^-7. Следовательно, такой кристалл уже относится к разряду твердых тел с «бесконечно большой поверхностью». И только при субмикроскопических размерах различия между его упругостью пара и аналогичной характеристикой бесконечно большого кристалла, а также стабильными и неустойчивыми гранями становятся ощутимыми, и пропорциональность о, / ft, будет реально наблюдаться, подчиняясь условию Гиббса — Вульфа. Таким образом, равновесная форма кристалла реализуется только на начальных стадиях кристаллизации. Для макроскопических кристаллов это возможно лишь при определенных условиях, поскольку исходный многогранник корректируется конкретными факторами, например специфической адсорбцией на межфазной границе, и другими осложняющими эффектами.

Термодинамическая трактовка равновесной формы кристалла получила развитие в молекулярно-кинетической концепции И. Странского и Р. Каишева (1939 г.), которые предложили использовать для ее нахождения метод средних работ отрыва частиц от конкретных граней. В упрощенном варианте рассматривается кристалл, и в первую очередь — кристалл Косселя, находящийся в равновесии с паровой фазой. Основной постулат состоит в том, что для всех граней равновесной формы давление насыщенного пара одинаково, как равны и вероятности растворения и образования плоских атомных сеток. В микромасштабе для всех поверхностных плоских сеток средняя работа отрыва cpjj каждой частицы имеет одну и ту же величину. Уравнение Томсона — Гиббса принимает вид.

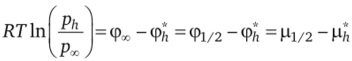
где ф" = ф_½ — работа отрыва одной частицы от полукристаллического положения; р_½ — химический потенциал частицы в положении у полукристалла; — средний химический потенциал частиц в плоскости кристаллической решетки, удаленных от центра на расстояние h.

Чтобы найти равновесную форму, исходят из кристалла с произвольной огранкой, удаляя все частицы с меньшими значениями ф по сравнению со средней работой отрыва. В частном случае грани (100) простого кубического кристалла с длиной N межатомных расстояний и с учетом лишь взаимодействия между первыми ближайшими соседями удаляют последовательно все атомы поверхностного слоя, начиная с одной из вершин, сохранив лишь два крайних ряда, т. е. (N — I)² частиц (рис. 2.39, а). На эту процедуру будет затрачена работа Зф{N- I)², так как при удалении каждого из атомов разрывается по три связи. Для отрыва любого из 2(N — 1) атомов оставшихся крайних рядов потребуется работа Зф (рис. 2.39, б), а при удалении последней угловой аннулируется всего одна связь (рис. 2.39, в).

Таким образом, работа отрыва в расчете на один атом удаляемого слоя, или средняя работа отрыва, составит.

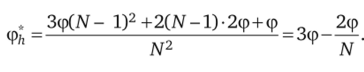
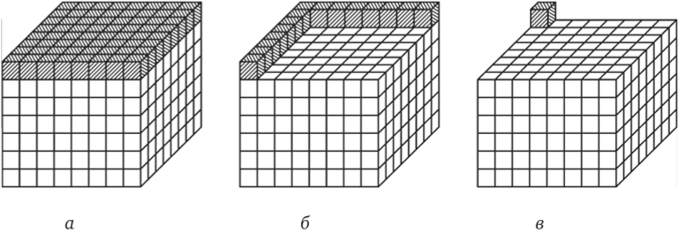
Рис. 2.39. Схема определения средней энергии отрыва частицы для грани.

куба кристалла Косселя Следовательно, принимая в расчет соотношение ф < ф^ < ф_½, выявляют все грани равновесной формы. Затем, варьируя их площади, можно прийти к ситуации, когда средняя работа отрыва одной частицы будет одинакова для всех граней. В использованном приближении для неполярного кубического кристалла на рис. 2.40, а это осуществлялось до тех пор, пока оставшиеся на поверхности частицы не оказались связанными так же прочно, как в полукристаллическом положении. В результате возникли простые формы {100}, {110} и {111}, образующие равновесный многогранник (рис. 2.40, б).

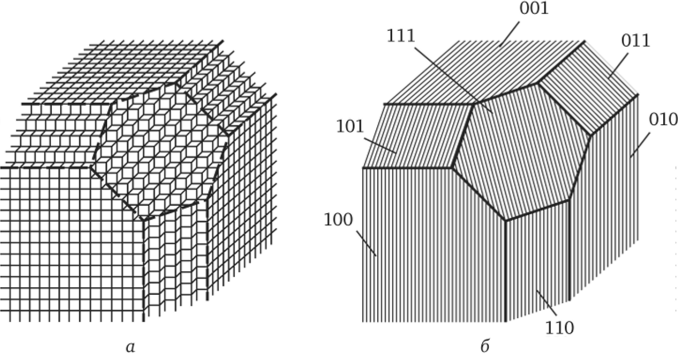
Рис. 2.40. Выявление равновесных граней {100}, {110}и{111} для кристалла Косселя с учетом взаимодействия между ближайшими частицами по методу Странского — Каишева.

Этот подход также идеализирован, так как далеко не всегда точно известна сила связи между частицами в той или иной обстановке. Он пренебрегает, например, и тепловыми колебаниями кристаллической решетки, что допустимо лишь в условиях низких температур — 0 К.

На практике определение равновесной формы означает, что если, например, поместить произвольно ограненный кристалл в насыщенный его пар или раствор, то произойдет регенерация неравновесных граней, в то время как при ненасыщенном состоянии системы различные грани испаряются (растворяются) в разной степени в силу их анизотропии. Экспериментальное получение равновесной формы мелких кристаллов полвека назад осуществляла Клия (1956 г.) на примере капелек (—30 мкм) насыщенного при —40°С водного раствора хлорида аммония, защищенных сильно гидрофобным полициклогексиленэтилом от возможного испарения компонентов кристаллизационной среды. При охлаждении до комнатной температуры на нагревательном столике микроскопа в помещенном между двумя покровными стеклами препарате появлялись дендритные кристаллы. Они впоследствии за несколько часов при постоянной температуре постепенно преобразовывались в сферообразные с множеством округлых «граней», форма которых уже не менялась в течение суток. Такой результат характерен для атомно-шероховатых поверхностей с несингулярными минимумами на полярной диаграмме удельной поверхностной энергии. Скорость самопроизвольного преобразования формы ограненного кристалла в равновесную в изотермических условиях существенно зависит от интенсивности массопереноса в кристаллизационной среде и температурных флуктуаций.

Основные грани, принадлежащие равновесной форме, как правило, реализуются и на формах роста. Поэтому рассмотренные методы применимы и для анализа реальной огранки. В целом же сведения о теоретической, структурно обусловленной и равновесной форме кристалла являются основополагающими для оценки влияния условий кристаллизации на их облик.