Экспоненциальная устойчивость. 
Теорема Красовского

Пусть система описывается уравнением.

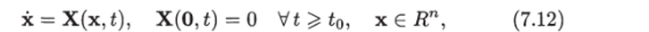
где правая часть является гладкой функцией: она непрерывно дифференцируема в области.

частные производные dXi/dxj удовлетворяют условию.

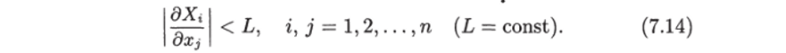
Решение уравнения (7.12) при начальном условии х (?о) = х°, как обычно, будем обозначать х (х°,?): х (х°,?о) = х°.

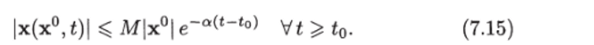
Определение 7.1. Положение равновесия (или невозмущенное движение) x (t) = 0 системы (7.12) называется экспоненциально устойчивым, если существуют положительные постоянные, а и М такие, что при |х°| < р/М возмущенное движение x (x°, t) удовлетворяет условию Если условие (7.15) выполняется при любых начальных условиях, то положение равновесия системы (7.12) называется глобально экспоненциально устойчивым или экспоненциально устойчивым в целом. Если линейная стационарная система устойчива, то она экспоненциально устойчива в целом.

Теорема 7.3 (теорема Красовского). Если положение равновесия системы (7.12) экспоненциально устойчиво, то существуют функция Ляпунова V (x, t) и положительные постоянные с* (г = = 1,2,3,4) такие, что выполняются неравенства

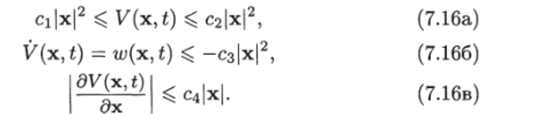
В случае экспоненциально устойчивой линейной стационарной или нестационарной системы существует квадратичная форма V (х) = = х^тВх или V (x, t) = х^тВ (?)х, удовлетворяющая условию теоремы Красовского. В случае экспоненциально устойчивой нелинейной системы соответствующая функция Ляпунова может быть неквадратичной формой.

При доказательстве теоремы Красовского используются две леммы, которые сейчас рассмотрим.

Лемма 7.1. Решение х (х°,t) уравнения (7.12) удовлетворяет условию

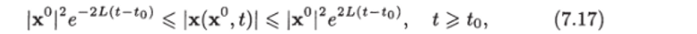
где L — постоянная, которая входит в (7.14).

Доказательство. По теореме о среднем значении Х*(х,t) = = х", ^гД^е звездочка сбоку производной обозначает ее значение в средней точке (а: 1, …, Si-i, xj, x*+i, …, х") (xj 6 [0, х*]). Поэтому имеем.

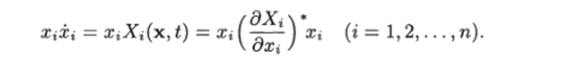
Используя условие (7.14), получаем.

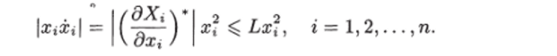
Суммируя это соотношение от 1 до п, получим.

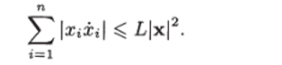
Используя это неравенство, находим.

Это неравенство можем записать в виде.

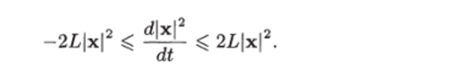
Интегрируя это неравенство от to до ?, получаем (7.17).

Лемма 7.2. Решение x (x°, t) уравнения (7.12) удовлетворяет условию

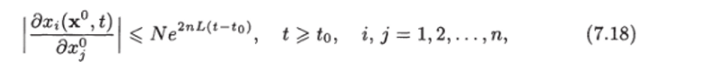
где N — положительная постоянная.

Доказательство. Подставив в уравнение (7.12) его решение х (х°,<), получим тождество.

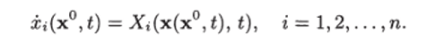
Продифференцировав это тождество по получим или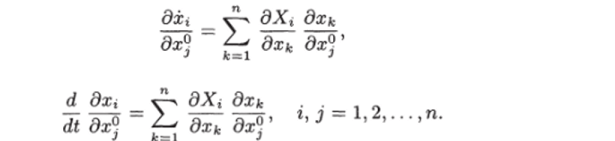

Из последнего равенства получаем.

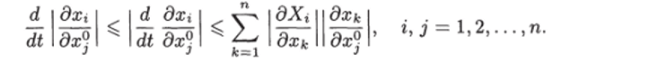
I дх I.

Если в какой-либо точке i! функция f (t) = недифференцируема, то в этой точке под производной понимается.

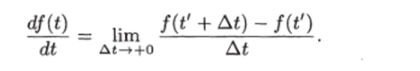
Просуммировав последнее неравенство от i = 1 до г = п, получим.

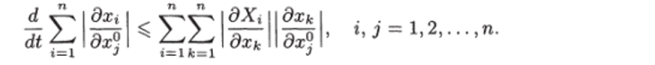
Введя обозначение = ~a~h и используя условие (7.14), последнее.

«=i I OXj I.

неравенство можем представить в виде или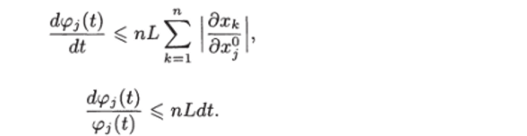

Проинтегрировав последнее неравенство от to до t, получим 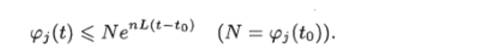Используя это неравенство, находим.

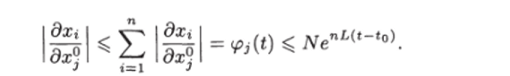
Лемма доказана.

Доказательство теоремы 7.3. Введем обозначениеТ= iln (Af/2),.

где а, М — постоянные, которые входят в (7.15). Рассмотрим функцию P (x, t), которая определяется следующим образом: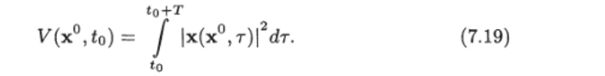

Функция V (x, t) получается из функции V (x°,?o) подстановкой х° = = х и to = t. Покажем, что эта функция удовлетворяет условиям теоремы. Используя (7.15) и (7.19), получаем.

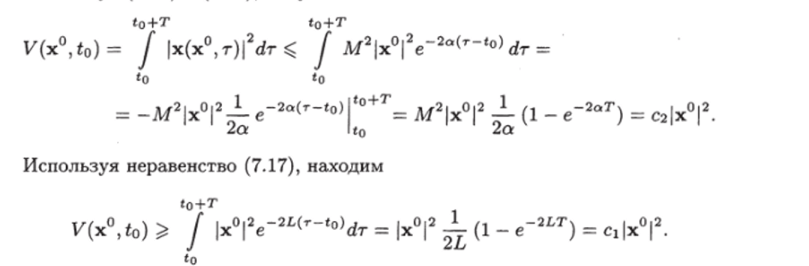
Из полученных неравенств следует, что функция V (x°, to) удовлетворяет условию ^

Подставив сюда х° = х, получим (7.16а).

Для получения соотношения (7.166) вычислим производную по времени функции V (x°,?o) в силу (7.12), подставив вместо х° решение х = х (х°,?) и to = t:

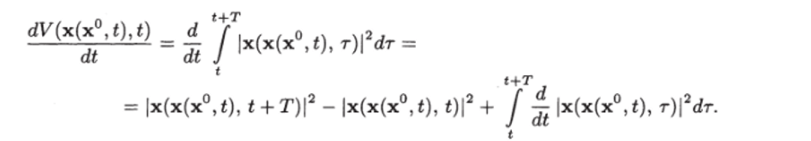
Функция x (x (x°, f), т) представляет траекторию изображающей точки, которая в момент r = t стартует из точки х (х°,?), а функция х (х (х°, t + At), г) — траекторию изображающей точки, которая в момент т = t + At стартует из точки х (х°, t + At). И так как эти траектории при т ^ t + At должны совпадать, то x (x (x°, t), г) = х (х (х°, t + At), т) и соответственно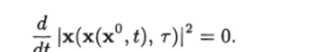

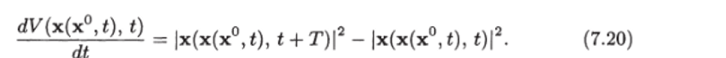
Поэтому производная функции Ляпунова принимает вид В силу (7.15) имеем.

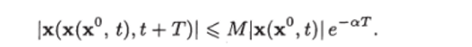
Используя тождество е^у1пг = z¹ и полагая осТ = 1п (М>/2), находим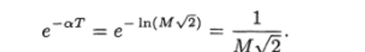

С учетом этого равенства последнее неравенство можно преобразовать к виду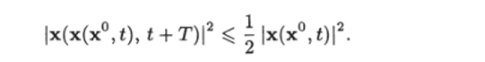

И так как x (x (x°, f), t) = х (х°,?), то из соотношения (7.20), получаем.

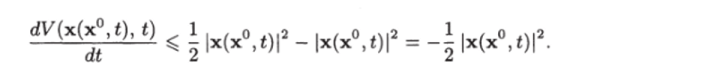
Поскольку х (х, t) = x (t)_y то, положив в последнем неравенстве х° = = х и сз = ½, получим неравенств (7.166).

Для доказательства справедливости последнего неравенства (7.16в) продифференцируем соотношение (7.19) по.

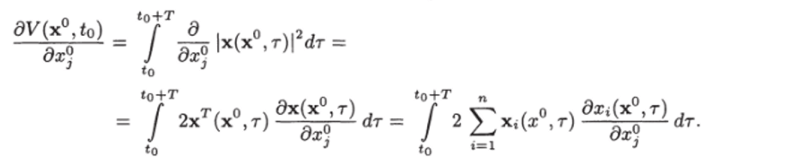
Отсюда, используя неравенства (7.15) и (7.18), получим.

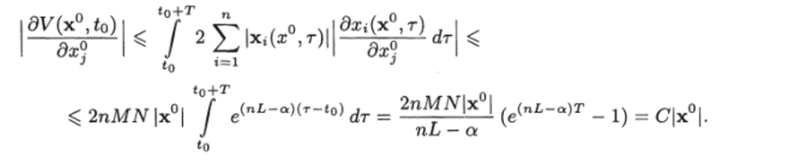
Если возвести обе части неравенства в квадрат и просуммировать, изменяя j от 1 до п, то получим или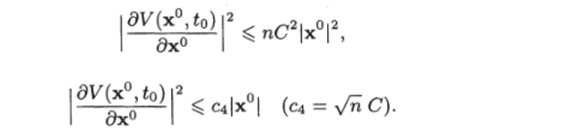

Подставив в это неравенство х° = х и to = ?, получим (7.16в).

Функция (7.19) является положительно определенной функцией, и ее производная по времени в силу уравнения (7.12) является отрицательно определенной (см. (7.166)). Теорема доказана.

Лемма 7.3. Производная квадратичной формы V (x) = x^TBx по х удовлетворяет условию

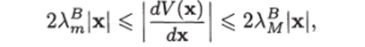
где А*, А* — минимальное и максимальное собственные значения матрицы В.

Отсюда получаем Доказательство. Найдем производную квадратичной формы по х:

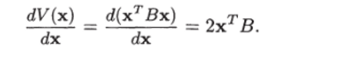
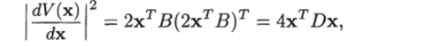
где D = ВВ^Т. Если минимальное и максимальное собственные значения матрицы D обозначить и соответственно, то согласно лемме 4.1 (см. (4.1)) имеем.

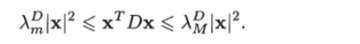
Следовательно, справедливо неравенство.

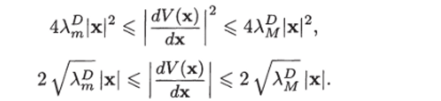
или Теперь достаточно показать, что собственные значения ЛР матрицы D равны квадрату собственных значений Af матрицы В: ЛР =.

= (Af)² (* = 1,2,.

Так как В является симметрической матрицей, существует неособая матрица Т такая, что произведение Т~¹ВТ представляет собой диагональную матрицу.

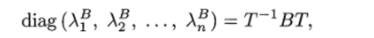
где Af (г = 1,2,…, п) — собственные значения матрицы В. Возведя в квадрат это равенство, получим.

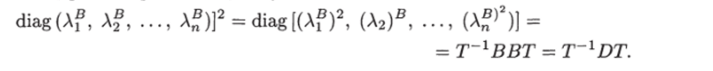
Отсюда следует, что собственные значения матрицы D равны квадратам собственных значений матрицы В, что и требовалось доказать.

Теорема 7.3 а. Если линейная стационарная система х = Ах устойчива, а положительно определенная квадратичная форма V (x) = х^гВх является ее функцией Ляпунова и производная от нее по времени в силу уравнения системы принимает вид

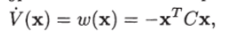
то в качестве констант Cj (г = 1,2,3,4) в соотношениях (7.16) можно принять.

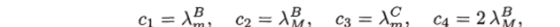
т. е. функция Ляпунопп. идоолетвопяет. следнюшим соотношениям:

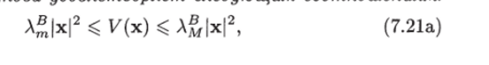
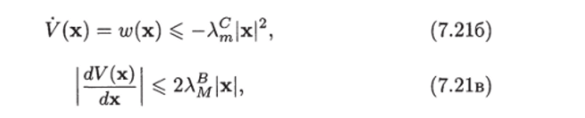
где А®, А^ —минимальное и максимальное собственные значения матрицы В, А^ — минимальное собственное значение матрицы С.

Доказательство. Неравенство (7.21а) непосредственно следует из леммы 4.1 (см. (4.1)). С помощью этой леммы также получаем неравенство (7.216): А^|х²| ^ х^тСх, или w (x) = -х^тСх ^ -А?|х²|. Неравенство (7.21 в) следует из леммы 7.3.