Принципы синтеза каскадной Е-Н-схемы замещения проводника прямоугольного сечения с нелинейными свойствами

На рис. 3.1 изображен проводник прямоугольного сечения, ширина сечения проводника равна 2а, высота сечения равна Ъ, причем Ь>>2а. Длина проводника в направлении оси ох неограниченно велика. Проводник изготовлен из ферромагнитного материала, удельная электрическая проводимость которого постоянна, а ферромагнитные свойства описываются кривой намагничивания по первым гармоникам.

Проводник в направлении оси ох обтекается синусоидальным током /, созданным сторонним источником. Известно, что при этих условиях в объеме проводника возникнет одномерное плоскопараллельное электромагнитное поле, которое формируется двумя плоскими Е-Н волнами, проникающими в него через боковые поверхности. При этом вектор электрической напряженности Е имеет только х-составляющую Ё_х, вектор магнитной напряженности Н имеет только у-составляющую Н_у (в дальнейшем для упрощения записи индексы х и у опущены). Электрическая и магнитная напряженности являются функциями координаты z. Поле ?(z) обладает четной, а поле.

H (z) — нечетной симметрией относительно оси симметрии проводника.

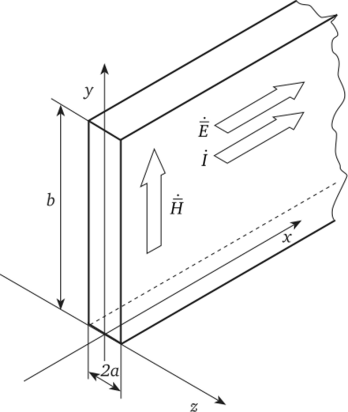
Рис. 3.1.

Поставим задачу получить аналитические выражения для электрической и магнитной напряженностей и на их основе сформировать каскадную схему замещения для расчета электромагнитного поля и эквивалентных интегральных параметров ферромагнитного проводника. Для решения этой задачи воспользуемся следующим алгоритмом:

• 1. Расчетную область представим в виде совокупности п параллельных полос, каждая к-я из которых имеет ширину h_k, удельную проводимость (как и во всем объеме) у и магнитную проницаемость [i_k. Значение магнитной проницаемости для /с-й полосы неизменно, но величина ц*. неизвестна.
• 2. Для каждой расчетной полосы запишем общие решения уравнения Гельмгольца для составляющих векторов Ё и Н.
• 3. Используя принципы схемной аппроксимации объемов, возбужденных электромагнитным полем^[1], приведем полученные общие решения для границ расчетной полосы к стандартным уравнениям четырехполюсника (А_к, В_к, С_к, D_k) и сформируем для него эквивалентную трехэлементную Е-Н-схему замещения.
• 4. Исходя из условий непрерывности составляющих векторов Ё и Н на границах смежных расчетных полос, сформируем нелинейную каскадную схему замещения для всего исследуемого объема.
• 5. Для имеющейся нелинейной каскадной схемы запишем систему уравнений Кирхгофа и рассчитаем ее как систему нелинейных алгебраических уравнений. В качестве расчетного инструмента на этом этапе удобно использовать средства компьютерной математики.
• 6. По известным значениям электрической и магнитной напряженности на поверхности проводника с помощью теоремы Пойнтинга рассчитаем комплексную мощность и комплексное сопротивление проводника переменному току.

Приступим к реализации вышеописанного алгоритма. На рис. 3.2 в исследуемой области (0к-я расчетная полоса Zj < z < z₂ (в дальнейшем индекс к для упрощения записи опущен). Ширина полосы h = z₂-z_x. На границах полосы обозначены составляющие векторов Ё и Н: при z-z_x Ё = Ё_Ь Н = Н_Х; при z = z₂ Ё = Ё₂, Н = Н₂.

Рис. 3.2.

Магнитная проницаемость полосы равна р, удельная электрическая проводимость полосы равна у, круговая частота равна со.

Уравнение (3.1) следует решить в общем виде, считая заданными значения магнитных напряженностей на границах полосы: Н (2]) = Я] и H (z₂) = H₂.

Общее решение дифференциального уравнения (3.1) сформируем в виде двух слагаемых таким образом, чтобы при z-z_{ обращалось в нуль одно слагаемое (или его первая производная), а при z = z₂ — другое. Поскольку ввиду четности решение должно содержать только гиперболические косинусы, имеем:

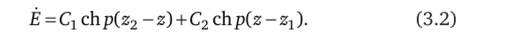
Магнитная и электрическая напряженности связаны между собой вторым уравнением Максвелла:

Вектор электрической напряженности в расчетной полосе удовлетворяет уравнению Гельмгольца:

Из (3.3) выражаем Я:

На границе z = z, обращается в нуль слагаемое при С₂ в выражении (3.4), следовательно.

Аналогично для границы z = z₂:

Таким образом, для векторов электрической и магнитной напряженностей получаем следующие выражения:

Из теории цепей известно^[2], что в пассивном четырехполюснике (рис. 3.3) напряжения и токи на входе (U_b /_а) и на выходе С0₂, /г) связаны уравнениями:

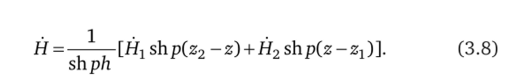
в которых постоянные четырехполюсника А, В, С, D удовлетворяют условию.

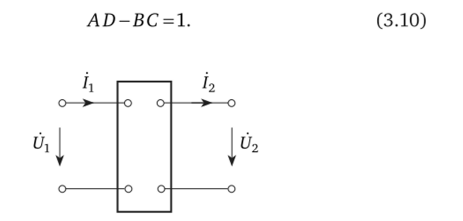
Рис. 3.3.

С помощью решения (3.7) запишем выражения для электрической напряженности на границах элементарной полосы (при z = z₁ и z = z₂), учитывая, что h = z₂-z₁.

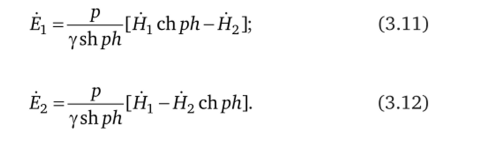
Преобразовывая (3.11) и (3.12), получим систему уравнений:

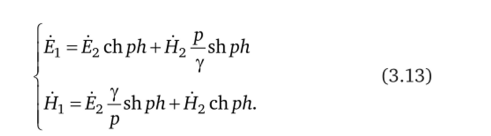
Эта система уравнений становится тождественной системе уравнений четырехполюсника (3.9), если считать электрическую напряженность Ё аналогом напряжения U, магнитную напряженность Я — аналогом тока /, и положить при этом.

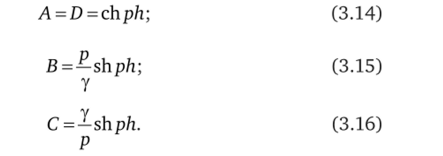
Коэффициенты А, В, С, D, вычисленные по (3.14)—(3.16), удовлетворяют также и условию (3.10). Таким образом, на границах элементарной расчетной полосы электрическая и магнитная напряженности удовлетворяют уравнениям четырехполюсника, и им может быть поставлена в соответствие либо П-, либо Т-образная схема замещения.

На рис. 3.4 показана Т-образная Е-Н-схема замещения расчетной полосы шириной h, сопротивления которой согласно теории четырехполюсников определяются выражениями.

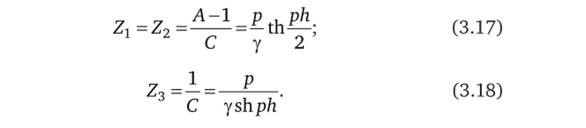
На смежных границах соседних расчетных полос электрическая и магнитная напряженности должны быть непрерывны. Это значит, что эквивалентные четырехполюсники, соответствующие расчетным полосам, должны быть включены в каскад, в результате чего и будет синтезирована каскадная Е-Н-схема замещения прямоугольного проводника шириной 2а. Наглядное представление об этом действии дает рис. 3.5.

В плоскости симметрии проводника (при z = 0) вектор магнитной напряженности меняет свое направление, кривая H (z) переходит через ноль, т. е. Н (0) = 0, поэтому входная ветвь крайнего левого четырехполюсника должна быть обесточена.

Внешняя граница крайней правой расчетной полосы примыкает к боковой поверхности проводника (при z = a). Магнитная напряженность на этой поверхности в соответствии с законом полного тока определяется величиной тока в проводнике / и высотой сечения проводника Ъ. Отсюда следует, что на внешние зажимы последнего четырехполюсника необходимо подключить источник Н₀, аналогичный источнику тока:

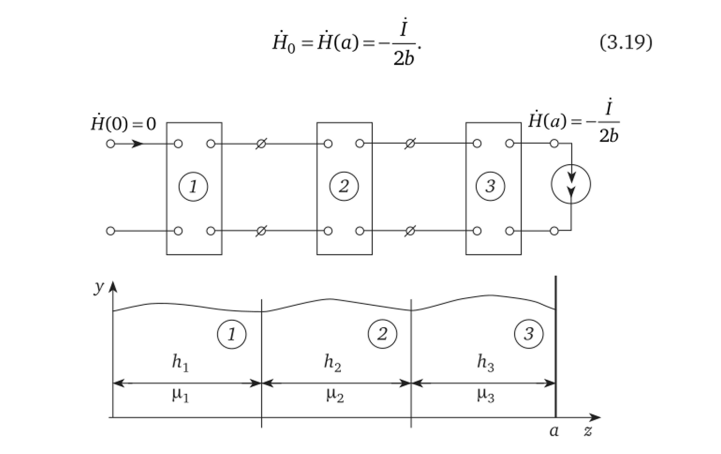
Рис. 3.5.

Все сопротивления в схеме замещения проводника являются комплексными, нелинейными, зависящими от магнитных напряженностей. Продольные и поперечные сопротивления в каждом четырехполюснике описываются одинаковыми выражениями (3.17) и (3.18) с той лишь разницей, что каждая расчетная полоса имеет свою конкретную ширину и свою магнитную проницаемость, а значит, и свой коэффициент распространения волны.

На каждом сопротивлении электрическая и магнитная напряженности связаны законом Ома:

Электрическая и магнитная напряженности, как и в любой электрической цепи, подчинены также законам Кирхгофа. Если составить систему уравнений Кирхгофа для полученной каскадной схемы, эта система будет представлять собой систему нелинейных алгебраических уравнений, которую можно решить численно.

Приведем пример составления системы уравнений Кирхгофа для случая трех расчетных полос.

Нелинейная каскадная Е-Н-схема, моделирующая электромагнитное поле в сечении ферромагнитного проводника прямоугольного сечения, представлена на рис. 3.6.

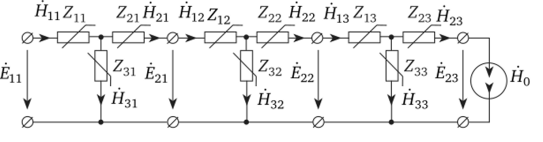
Рис. 3.6.

Для цепи на рис. 3.6 можно составить систему из четырех независимых уравнений Кирхгофа. Неизвестных магнитных напряженностей также четыре. Система уравнений по законам Кирхгофа имеет вид:

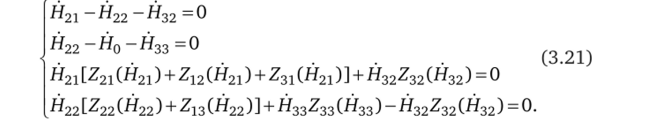
После решения системы уравнений (3.21) относительно неизвестных магнитных напряженностей можно определить электрические напряженности на границах расчетных полос:

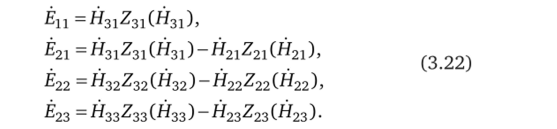
Вектор Пойнтинга на поверхности проводника:

Комплексная мощность, выделяющаяся в проводнике (на единицу длины в направлении оси ох):

Комплексное сопротивление проводника на единицу длины:

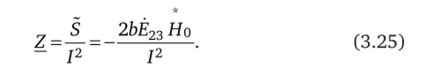
Мнимая часть комплексной мощности (3.24) представляет собой энергию магнитного поля, заключенную только внутри объема проводника, поэтому комплексное сопротивление, вычисленное по выражению (3.25) есть внутреннее сопротивление.

• [1] Инкин А. И. Электромагнитные поля и параметры электрических машин.
• [2] Теоретические основы электротехники / Л. Р. Нейман [и др.].