Модель Вольтерра. 
Теория вероятностей и математическая статистика. 
Математические модели

В качестве второго примера рассмотрим классическую вольтерровскую модель «хищник — жертва», которая была предложена В. Вольтерра для объяснения периодических изменений числа особей. Модель впервые опубликована в работе V. Volterra «Variozionie fluttuasionie del numero d’individui in specie animali conviventi». Mem. Acad. Lincei. Vol. 2. — P. 31 — 113, 1924^[1].

Пусть в некотором замкнутом районе живут хищники и жертвы, например волки и зайцы. Зайцы питаются растительной пищей, имеющейся всегда в достаточном количестве. Волки могут питаться лишь зайцами. Обозначим число зайцев (жертв) — х, а число волков (хищников) — у. Так как количество пищи у зайцев неограниченно, можно предположить, что они размножаются со скоростью, пропорциональной их числу:

Если рождаемость зайцев превышает их смертность, то г > 0. Выражение (5.24) соответствует автокаталитической реакции первого порядка.

Пусть убыль зайцев пропорциональна вероятности встречи зайца с волком, т. е. пропорциональна произведению ху. Можно предположить по аналогии с бимолекулярными реакциями, где вероятность появления новой молекулы пропорциональна вероятности встречи двух молекул, что и количество волков нарастает тем быстрее, чем чаще происходят их встречи с зайцами, а именно пропорционально ху.

Кроме того, имеет место процесс естественной смертности волков, причем скорость смертности пропорциональна их количеству.

Эти рассуждения приводят к системе уравнений для изменений численности зайцев-жертв х и волков-хищников у:

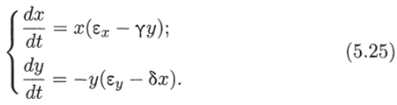
Система имеет два стационарных решения. Одно из них — нулевое: хо — 0, уо = 0. Линейный анализ устойчивости показывает, что эта точка всегда представляет собой седло. Покажем, что система уравнений (5.25) также имеет на фазовой плоскости переменных ху ненулевую особую точку типа «центр». Координаты этой точки: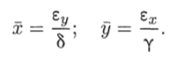

Так как все параметры ?_ж, е_у, у, 8 положительны, точка (ж, у) расположена в положительном квадранте фазовой плоскости. Линеаризация системы вблизи этой точки дает:

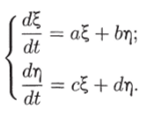
Коэффициенты в этих уравнениях выражаются в соответствии с (5.18) через частные производные правых частей уравнений системы (5.25) формулами: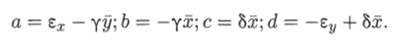

Здесь ?, т) — отклонения численностей от их стационарных значений х, у: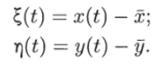

Для нулевого стационарного состояния характеристический определитель имеет вид:

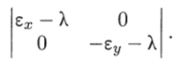
Корни соответствующего характеристического уравнения: Xi = = е_х, Х2 = —Еу Тип нулевой особой точки — седло.

Характеристический определитель матрицы коэффициентов системы для ненулевого стационарного состояния имеет вид:

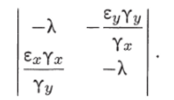
Характеристическое уравнение:

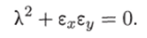
Корни этого уравнения чисто мнимые:

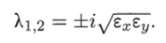
Таким образом, исследование системы показывает, что траектории вблизи ненулевой особой точки являются концентрическими эллипсами, а сама особая точка — центром. Можно показать, что изученная модель Вольтерра и вдали от особой точки имеет замкнутые траектории, хотя форма этих траекторий уже отличается от эллипсоидальной, и определяется параметрами системы (рис. 5.11).

Изменения численности жертв и хищников во времени представляют собой колебания, причем колебания численности хищников отстают по фазе от колебаний жертв.

Особая точка типа «центр» устойчива по Ляпунову, но не асимптотически. Покажем на данном примере, в чем это проявляется. Пусть колебания x (t) и y (t) происходят таким образом, что изображающая точка движется по фазовой траектории 1 (см. рис. 5.11).

В момент, когда точка находится в положении Mi, в систему добавляется извне некоторое число особей у, такое, что изображающая точка переходит скачком из точки Mi в точку М2.

Если после этого систему предоставить самой себе, то колебания x (t), y (t) уже будут происходить с большими амплитудами, чем прежде, и изображающая точка будет двигаться по траектории 2. Это и означает, что колебания в системе неустойчивы: они навсегда изменяют свои характеристики при внешнем воздействии.

В дальнейшем будут рассмотрены модели, описывающие устойчивые колебательные режимы, и показано, что на фазовой плоскости такие асимптотически устойчивые периодические движения описываются предельными циклами.

На рис. 5.12 приведены кривые колебаний численности пушных зверей по данным компании Гудзонова залива о числе заготовленных шкурок. Во всех классических учебниках в течение многих лет колебательный характер этих изменений приводили как подтверждение гипотез, положенных в основу модели Вольтерра, которая только что была рассмотрена. Действительно, периоды колебаний численности зайцев (жертв) и рысей (хищников) примерно одинаковы и составляют порядка 9 —10 лет. При этом максимум численности зайцев опережает, как правило, максимум численности рысей на один год. Можно полагать, что мы видим регулярные колебания, осложненные случайными факторами, связанными с погодой и пр.

Однако возможна и другая интерпретация этих данных наблюдений на основе моделей детерминированного хаоса. Дискретные модели такого типа рассматривались в гл. 1 (см. 1.4).

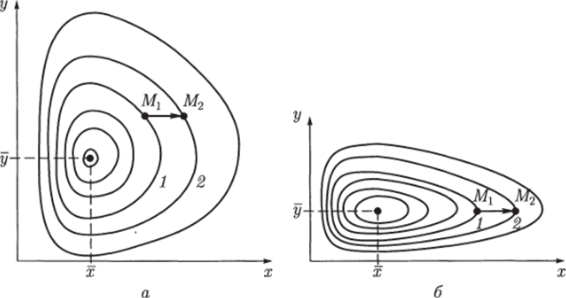
Рис. 5.11. Фазовый портрет системы (5.25). Особая точка типа «центр»:

а — параметры системы: е* = 4, у_ху = 0,3, е_у = у_ух = 0,4; б — параметры системы: г_х = 2, у_ху = 0,3, t_y = у_ух = 0,4.

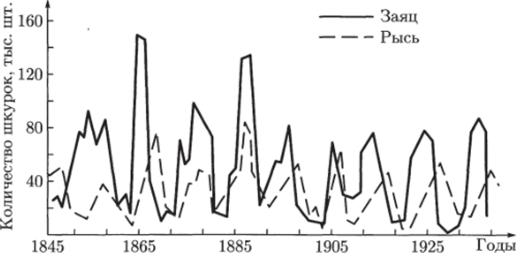
Рис. 5.12. Кривые численности зайца и рыси в Канаде [К. Вилли,.

В.Детье, 1974].

Непрерывные модели популяционной динамики, приводящие к детерминированному хаосу, будут изучены далее.

Серьезным недостатком модели Вольтерра является неустойчивость решений по отношению к малым случайным воздействиям, приводящим к изменению переменных. Кроме того, в силу «негрубости» этой системы произвольно малое изменение вида правых частей уравнений (величин параметров системы) приведет к изменению типа особой точки и, следовательно, к изменению характера фазовых траекторий.

Поскольку природные системы подвергаются огромному количеству случайных воздействий, реалистическая модель должна быть по отношению к ним устойчивой. Поэтому негрубые системы не могут давать адекватное описание природных явлений.

Различные модификации рассмотренной системы, изученные самим Вольтерра и другими авторами, лишены этих недостатков. Наиболее широко известные из них будут изучены в 5.6. Здесь остановимся на модели, которая учитывает самоограничение в росте обеих популяций. На ее примере видно, как может меняться характер решений при изменении параметров системы.

Итак, рассмотрим систему:

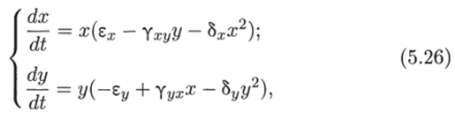
которая отличается от системы (5.25) наличием в правых частях членов: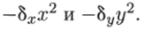

Эти члены отражают тот факт, что численность популяции жертв не может увеличиваться до бесконечности даже в отсутствие хищников в силу ограниченности пищевых ресурсов, ареала существования и пр. Такие же «самоограничения» накладываются на популяцию хищников.

Система (5.26) имеет четыре стационарных решения, для трех из них либо численность обоих видов, либо численность одного из видов равна нулю. Анализ показывает, что нулевое решение представляет собой неустойчивый узел. Рассмотрим систему алгебраических уравнений, решение которых дает координаты стационарного состояния, ненулевого для численностей обоих видов. Эта система получается приравниванием нулю выражений в скобках в правых частях системы (5.26):

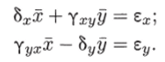
Стационарное решение:

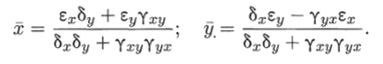
Анализ корней характеристического уравнения показывает, что стационарное решение в зависимости от соотношения коэффициентов может быть либо устойчивым фокусом, либо устойчивым узлом (рис. 5.13).

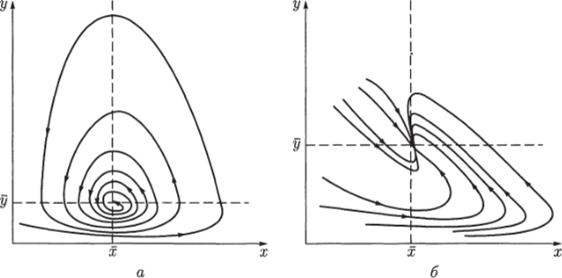
Рис. 5.13. Фазовый портрет системы (5.26):

а — устойчивый фокус, параметры системы: Сх = 2, у_Ху = 18, 8* = 1, с_у = 3, Уух = 5, Sj, = 1; б — устойчивый узел, параметры системы: е_х = 2, у_ху — 1, 5а: ⁼ 1, Еу = 3, Yyx ⁼ 1, 5у = 1.

И в том и в другом случае решение устойчиво к малым изменениям правых частей уравнений. Таким образом, самоограничение популяции приводит к устойчивости ее численности.

Важно отметить, что рассмотренные простейшие вольтерровские модели не могут описывать устойчивые колебания с постоянным периодом и амплитудой. Для описания таких колебаний необходимы нелинейные модели, имеющие на фазовой плоскости предельный цикл (см. 5.6).

• [1] Вольтерра В. Математическая теория борьбы за существование. — М.: Наука, 1976.