Устойчивость решений по ляпунову

Определение устойчивости. Сведение к исследованию устойчивости нулевого решения

Рассмотрим нормальную систему.

(t, у)? GcRx Y" , /: G —> Y", G — открыто в R х Y", f е C (G, У"), / е € loc Lip_iy(G).

Фиксируем (т, г|) е G. Будем обозначать через cp (f; т, р), где t е /(т, р) с R, полное решение системы (5.1), такое что.

Будем рассматривать решение |/(1), определенное на интервале [ ?₀; +°°). Обозначим г/₀ = [/(/:₀) начальное значение, таким образом, (Г₀; у₀) — начальная точка. Итак, |/(?) = ф (/; t₍₎, г/₀) при t е |/₀; +оо).

Рассмотрим некоторое решение, будем его называть невозмущенным (рис. 5.1).

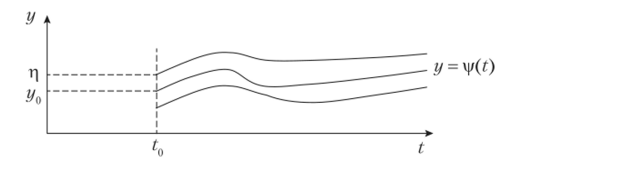
Рис. 5.1.

Определение 5.1. Невозмущенное решение ср (?; t_Q, у₀), t е [?₀; +°°) называется устойчивым по Ляпунову, если для любого е > О существует такое 8 > 0, что для любого р, такого что ||р — г/о II ^< 5, для любого t е [f₀; +°°) выполняется условие ||ф (Г; t₀, р) — ф(1; t₀, г/₀)|| < в.

Другими словами, решения е-близки, если начальное значение 8-близко к у₀ (рис. 5.2).

Грубо говоря, решение называется устойчивым по Ляпунову, если все решения, начинающиеся близко от |/(?), остаются близкими к нему. У маятника два положения равновесия. Верхнее — это неустойчивое движение, оно не реализуется, всегда есть какая-то ошибка, может быть, скорость начальная какая-то ненулевая. Нижнее положение маятника — устойчивое равновесие.

Рис. 5.2.

Определение 5.2. Решение, которое не является устойчивым по Ляпунову, является неустойчивым решением, или неустойчивым движением.

Определение 5.2'. Невозмущенное решение ф (?; ?₀, у₀), t е [f₀; +°°) называется неустойчивым по Ляпунову, если Зе > 0: VS > 0 3? е [ /;₀; +°°): Зтр

(Ил — Уо1 < ^{8 &} Цф (С tо> л) — ф (?; <6, Уо) И * <0;

Тогда определение устойчивого движения можно дать как вторичное определение.

Определение 5.1'. Невозмущенное решение называется устойчивым по Ляпунову, если оно не является неустойчивым по Ляпунову.

Определение 5.3. Рассматриваемое невозмущенное решение называется асимптотически устойчивым, если оно устойчиво по Ляпунову и является притягивающим, т. е. существует такое Д > 0, что для любого rj, такого что ИлУо11 < ^д— ^веР^1Ю> что || ф (?; t₀, г|)-cp (/;t₀, у₀)|| >0.

Рассмотрим отклонение Z — у — i (t) решения у от невозмущенного решения vp. Тогда Z = у- vp. Таким образом, имеем.

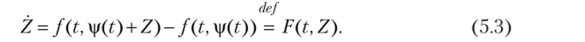
Очевидно, что если у удовлетворяет уравнению (5.1), то Z удовлетворяет уравнению (5.3). Обратно, если Z удовлетворяет уравнению (5.3), то у = Z + р (^) удовлетворяет уравнению Z = y-if = f (t, y)-i, или у = f (t, у), т. е. уравнению (5.1).

Ясно, что Z s 0 является решением уравнения (5.3). Будем называть это решение нулевым, или 0-решением.

Лемма 5.1. Тин устойчивости решения |i (t) системы (5.1) совпадает с типом устойчивости 0-решения системы (5.3).

Доказательство. Рассмотрим (вместо у) функцию Z = ф (?; ?₀, г|) — ф (?). Мы уже видели (непосредственно перед формулировкой леммы), что если у — решение системы (5.1), то у — ф (?) — решение системы (5.3), и наоборот. А ф (?; ?₀, Г|) — решение системы (5.1), поэтому Z — решение системы (5.3). Обозначим C, = Z₍__t =Ц-у₀, где у₀ = (/(?₀) — То, что нулевое решение (5.3).

является устойчивым, значит, что ||ф (?; ?₀, р) — ф (?)| < е, как только I1¹1 ^- 1/о11 ^< S. Но эго и есть неравенство из определения 5.1, т. е. устойчивость по Ляпунову уравнения (5.1). Последнее показывает, что 0-решение системы (5.3) устойчиво, но Ляпунову тогда и только тогда, когда усгойчиво по Ляпунову решение (5.1) |/(?) — Ясно также, что 0-решение системы (5.3) является притягивающим тогда и только тогда, когда притягивающим является решение 1|/(?) уравнения (5.1). Лемма доказана.

На основании леммы 5.1 все результаты можно формулировать для нулевого решения системы (5.3).