Линейные стационарные системы разностных уравнений

Определение 7.16. Линейной стационарной системой разностных уравнений называется система вида.

где А — заданная квадратная числовая невырожденная (п х и)-матрица; f_k — заданная вектор-функция с п компонентами на множестве N₀; x_k — неизвестная вектор-функция с п компонентами; k е N₀.

Одновременно с системой (7.20) будем рассматривать линейную однородную стационарную систему разностных уравнений.

Система (7.21) всегда имеет тривиальное решение^ = 0. Будем искать нетривиальные решения в виде.

где X Ф 0; h — ненулевой вектор с п компонентами. Подставляя х_к из выражения (7.22) в формулу (7.21), получаем алгебраическую систему уравнений Ah = Xh.

Это означает, что X должно быть собственным числом матрицы^4, а /г — соответствующим собственным вектором. Таким образом, X должно быть корнем характеристического уравнения det (A — ХЕ) = 0.

Аналогично соответствующим теоремам относительно решений систем дифференциальных уравнений доказываются следующие теоремы для разностных уравнений.

Теорема 7.15. Если существует базис пространства К" из собственных векторов h, h₂, …, h" матрицы, А и Х_ь …, Х_п — соответствующие им собственные числа, то общее решение системы (7.21) имеет вид

где С_х, С₂,…, С_п — произвольные постоянные.

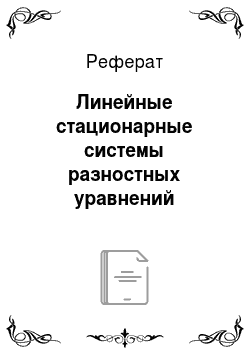
Доказательство. Так как h_x, h₂…h_n — базис в М", то каждое решение системы (7.21) имеет вид х_к = C,_xkh_x + C,_2kh₂ + … + ^гД^е координаты ^_хк, С,_2к, •••> Си* находятся подстановкой х_к в систему (7.21). Имеем.

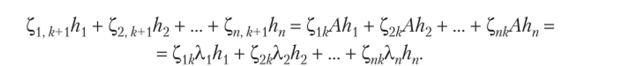
Получаем, что для всех ie N₀ верно, что Ci,*+i ⁼ *iC_№ С2, *+1 =^с₂*;

Си, *+1 ^— ^нСн*Решая эти уравнения, находим, что Ci* = C7_tA.*,⁼ ^2^2'-'^пк ⁼^Л", где C_lt С₂,…, С_п — произвольные постоянные. Следовательно, все решения системы (7.21) задаются формулой.

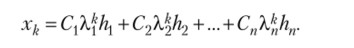
Теорема 7.16. Общее решение линейной однородной стационарной системы разностных уравнений (7.21) имеет вид

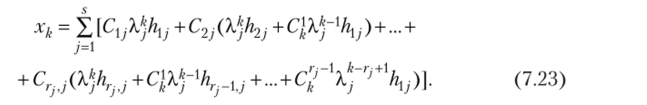
Доказательство. Как следует из параграфа 7.4, общее решение системы (7.21) имеет тцх_к = А^кС, где С — произвольный числовой и-вектор. Если жорданов базис состоит из s жордановых цепочек длины г-. h_ij, h₂j,~., h_l., j,.

соответствующих собственным значениям h, j =1,2,…, s (среди которых могут быть одинаковые), то г₍ + г₂ + … + r_s — п.

Разложим вектор С по жорданову базису пространства R" и подставим это разложение в формулу для х_к. Получим.

гдeCj, C₂j,.;C_r.j — произвольные постоянные, являющиеся компонентами разложения вектора С но жорданову базису, у =1,2, …, s. Посмотрим, как действует А^к на векторы жорданова базиса. Пусть собственному числу X матрицы А соответствует жорданова цепочка h_u h₂,…, h_r Методом математической индукции можно показать, используя определение собственного и присоединенных векторов, что.

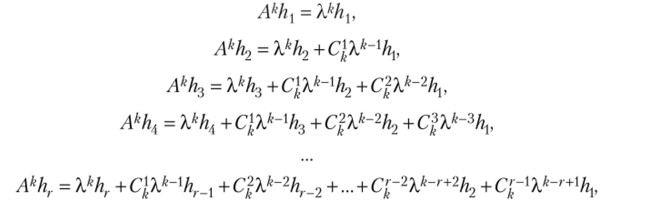
где С_к — число сочетаний из k по т, т = 1, 2, …, г — 1. Отсюда получаем формулу (7.23), что доказывает теорему 7.16.

Замечание 7.7. В формуле (7.23) содержится п произвольных постоянных, так как i + г₂ + … + r_s = п.

Теорема 7.17. Пусть в неоднородной линейной стационарной системе разностных уравнений (7.20) /_к = x^kP_s(k), где р — заданное ненулевое вещественное число, a PJJt) — многочлен степени s, коэффициентами которого являются заданные вещественные п-мерные числовые векторы. Если число р не является собственным значением матрицы А, то существует частное решение системы (7.20) вида х?⁰⁾ = |а^л'(2_ч (/^), где Q_s(k) — многочлен той же степени s, что и многочлен P_s(k), коэффициенты которого находятся подстановкой х?⁰⁾ в систему (7.20).

Доказательство. Пусть P_s(k) = k^sp₀ + k^s_ip_x + … + p_s, Q_s(k) = k^sq₀ + + k^s~^xq_x + … + q_s, где p₀ * 0, p_x, p₂, … p_s — заданные числовые «-мерные векторы, а 0, q_x, …, q_s — подлежащие определению из системы уравнений (7.20) неизвестные числовые «-мерные векторы.

Подстановка х?⁰⁾ в систему уравнений (7.20) дает равенство.

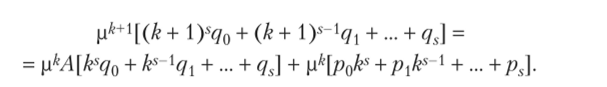
После сокращения на р* видим, что коэффициент при k^s удовлетворяет уравнению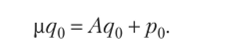

Так как р не является собственным значением матрицы А, существует обратная матрица (рТ — А) и мы находим q₀ = (рЕ — А)~¹р_(у

Поскольку р₍₎Ф 0, то и q₀* 0, значит, Q_s(k) — многочлен степени s.

Пример 7.13.

Решим систему уравнений.

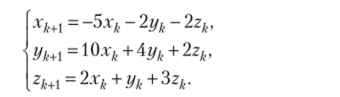
Решение. Находим собственные числа и собственные векторы матрицы системы.

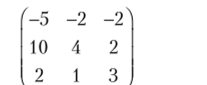
— 1) Г-1) (о^>

и получаем: Я., = -1, л₂ = 1, л_:) = 2, /?, = 2, h₂ = 4, /;₃ = 1. Таким образом, общее решение заданной системы имеет вид.

где С, С₂, С, — произвольные постоянные.

Решим систему уравнений.

Решение. Для матрицы системы находим собственные числа = -2 кратности 1 и Х₂ ⁼ 3 кратности 2. Собственному числу соответствует собственный век;

тор 1ц = 0, а собственному числу Х₂ — собственный вектор h₂= 1 и присоеди;

'-Г ценный вектор = 1 .

[о,.

Следовательно, общее решение заданной системы имеет вид

где С*, С₂, С₃ — произвольные постоянные.

Пример 7.15.

Решим систему уравнений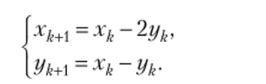

Решение. Матрица системы имеет собственные числа = iД₂ = - i. Им соответствуют сооственпые векторы.

Общее комплексное решение системы 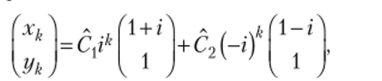имеет вид где С, и С₂ — произвольные комплексные постоянные. Выделяя вещественную и мнимую части решения, получаем.

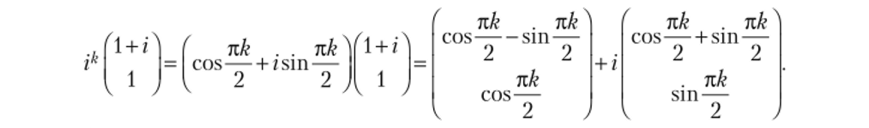
Общее вещественное решение заданной системы имеет вид.

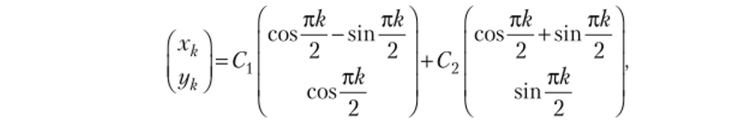
где C_v С₂ — произвольные вещественные постоянные.

Пример 7.16.

Решим систему уравнений.

Г¹ -О.

Решение. Матрица системы ^ ^ q имеет собственные числа Х₂ = 2.

Соответствующие им линейно независимые собственные векторы.

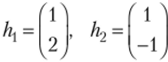
Общее решение заданной системы имеет вид.

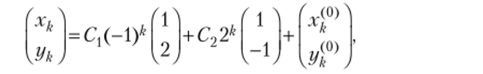
где Cj, С₂ — произвольные постоянные, а столбец из х?⁰⁾ и задает частное решение заданной системы разностных уравнений. Согласно теореме 7.17 частное решение имеет вид.

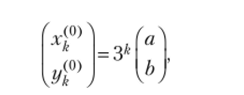
где коэффициенты а и b можно найти методом неопределенных коэффициентов. Подставляя это решение в систему разностных уравнений, находим.

Отсюда находим, что а = 1, b = -1. Следовательно, общее решение заданной системы.

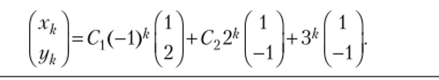
Фундаментальная матрица решений. Понятие фундаментальной матрицы решений в случае системы разностных уравнений вводится точно так же, как и в случае систем дифференциальных уравнений.

Очевидно, что x_k = А^к является решением матричного уравнения (7.21) и матрица A^k является фундаментальной матрицей решений линейной стационарной системы разностных уравнений (7.21). Пусть J — жорданова форма матрицы A, S — матрица перехода (невырожденная), тогда А = SJS~^{, Ab = SJ^kS~AbS = SjK

Пусть J = diag{Aj, Л₂, A_w}, согласно теореме Жордана каждая клетка имеет вид.

где порядок матрицы r_k не превосходит кратности соответствующего собственного числа Х/_г Тогда очевидно, что.

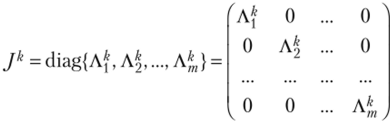
Посмотрим, что представляет собой один блок Af. Опустим индекс у Л, и рассмотрим просто жорданову клетку Л порядка г. Она представляет собой сумму двух матриц.

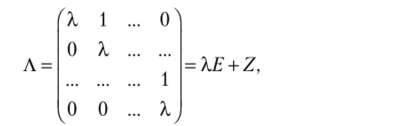
Таким образом, А² — Ш + 2XEZ + Z², A^:s = Х³Е + 3*E?Z + 3XEF- + Z³ = = Х*Е + 3ХЧ + 3²? + Z³ и т.д.,.

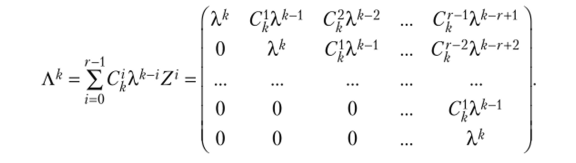
Замечание 7.8. Если А^к — фундаментальная матрица решений системы (7.21), а 5 — невырожденная матрица, то A^kS — также фундаментальная матрица решений системы (7.21). Но A^kS = SJ^k, поэтому самый простой способ решить систему (7.21) — это привести матрицу А к жордановой форме и выписать фундаментальную матрицу решений SJ^k. Например, если порядок системы уравнений п = 3 и характеристическое уравнение имеет единственный корень кратности 3, которому соответствует система из единственного собственного вектора, то фундаментальная матрица решений выглядит следующим образом:

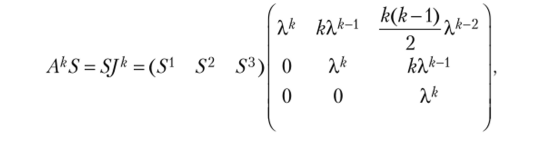
где S^{, S², S³ — соответственно собственный и два присоединенных, или корневых, вектора высоты 1 и 2 соответственно, или столбцы матрицы S_y т. е. решения следующих уравнений: (А — XE) S¹ = О, (А — XE^S² = 5¹, (А — ХЕ)№ = S².