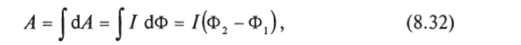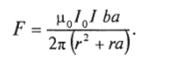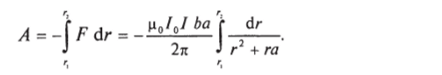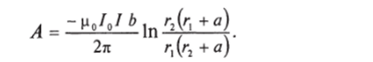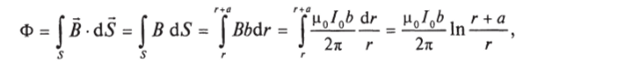Магнитный поток. 
Физика. 
Механика. 
Электромагнетизм

Величина.

где интеграл вычисляется по некоторой поверхности S_y называется магнитным потоком через поверхность S (рис. 8.28).

Возьмем трубку, образованную силовыми линиями поля В (рис. 8.29).

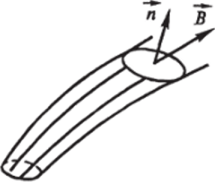
Рис. 8.28 Рис. 8.29

Интеграл J В dS по любому сечению этой трубки даст одну.

s

и ту же величину. Это позволяет интерпретировать магнитный поток как число силовых линий поля В, пересекающих поверхность S.

Работа по перемещению контура с током в магнитном поле

При малом перемещении или деформации контура с током совершается работа где с! Ф — изменение магнитного потока. Полная работа будет.

если / = const (для этого необходимо по крайней мере, чтобы контур перемещался достаточно медленно).

Задача 8.8. Найти работу по перемещению контура в поле прямого проводника (см. рис. 8.27).

Решение. Сила, действующая на контур, согласно (8.29), равна.

Работа по перемещению контура от г, до г_г будет 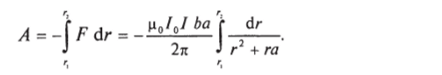Вычисляя интеграл, получим.

С другой стороны, магнитный поток через площадь контура равен.

и формула (8.32) дает тот же результат. (При вычислении потока учтено, что В dS = В dS, так как вектор В сонаправлен с вектором d-S¹, площадь контура разбивается на полоски шириной dr и площадь dS = bdr.)