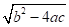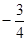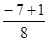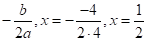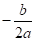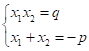Решение квадратных уравнений по формуле

Вывод формулы:

Умножим обе части уравнения.

ах² + bх + с = 0, а? 0,.

на 4а и следовательно имеем:

• 4а²х² + 4аbс + 4ас = 0.
• ((2ах)² + 2ах · b + b²) — b² + 4ас = 0,
• (2ах + b)² = b² — 4ас,
• 2ах + b = ±

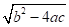
2ах = - b ±.

Х_1,2 =.

Решим уравнения:

а) 4х²+ 7х + 3 = 0.

а = 4, b = 7, с = 3, D = b² — 4ас = 7² — 4· 4 · 3 = 49 — 48 = 1, D >два разных корня;

х =, х =; х =, х₁ =, х =, х₂ = -1.

Таким образом, в случае положительного дискриминанта, т. е. при b² — 4ас?0 уравнение ах² + bх + с = 0 имеет два различных корня.

б) 4х² — 4х + 1 = 0,.

а =4, b= - 4, с = 1. D = b² — 4ас= 16 — 4•4•1 = 0, D = 0, один корень;

х=.

Итак, если дискриминант равен нулю, т. е. = b² — 4ас= 0, то уравнение ах² + bх + с = 0 имеет единственный корень, х =.

в) 2х² +3х + 4 = 0, а =2, b= 3, с = 4, D = b² — 4ас= 9 — 4•2•4 =9 — 32 = - 13,.

D < 0. Уравнение не имеет корней.

Итак, если дискриминант отрицателен, т. е. = b² — 4ас< 0, то уравнение.

ах²+ bх + с = 0 не имеет корней.

Решение уравнений с использованием теоремы Виета

а) Как известно, приведенное квадратное уравнение имеет вид.

х² + px + q = 0. (1).

Его корни удовлетворяют теореме Виета, которая при а = 1 имеет вид.

Отсюда можно сделать следующие выводы (по коэффициентам p и qможно предсказать знаки корней).

а) Если свободный член qприведенного уравнения (1) положителен (q >0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p.

Если p>0, то оба корня отрицательные, если p<0, то оба корня положительны.

Например, х² — 3х + 2 = 0; х₁ = 2 и х₂ = 1, так как q = 2 > 0 и p = - 3 <0;

х² +8х + 7 = 0; х₁ = - 7 и х₂ = - 1, так как q = 7 > 0 и p = 8 >0.

б) Если свободный член qприведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p<0, или отрицателен, если p>0.

Например, х² + 4х — 5 = 0; х₁ = - 5 и х₂ = 1, так как q = — 5<0 и p = 4 > 0;

х² — 8х — 9 = 0; х₁ = 9 и х₂ = - 1, так как q = — 9<0 и p = - 8 >0.

б) Теорема Виета для квадратного уравнения.

ах² +вх +с = 0.

имеет вид.

Справедлива теорема, обратная теореме Виета:

Если числа х₁ и х₂ таковы, что х₁+х₂ = -р, х₁х₂ = q, то х₁ и х₂ — корни квадратного уравнения квадратный уравнение номограмма х² +рх + q = 0.

Эта теорема позволяет в ряде случаев находить корни квадратного уравнения без использования формулы корней.

1. Решить уравнение х² — 9х + 14 =0.

Попробуем найти два числа х₁ и х₂, такие, что х₁ +х₂ = 9.

х₁х₂ = 14.

Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.

2. Решить уравнение х² +3х — 28 = 0.

Попробуем найти два числа х₁ и х₂, такие, что х₁ +х₂ = - 3.

х₁х₂ = - 28.

Нетрудно заметить, что такими числами будут — 7 и 4. Они и являются корнями заданного уравнения.