Сферические волны. 
Электромагнитные волны

У сферической волны фаза постоянна на поверхности сферы. Задача имеет сферическую симметрию. Ее следует решать в сферической системе координат. Электрическое и магнитное поле не зависят от угловых координат и. Выберем систему координат так, чтобы электрическое поле было направлено по оси. Запишем однородное уравнение Гельмгольца (2.2.1) в среде без потерь в сферической системе координат (см. П2.28, приложение П2) для единственной составляющей электрического поля Е.

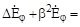
. (3.22).

Учтем, что производные по обеим угловым координатам и равны нулю:

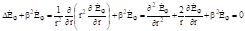
.(3.23).

Это уравнение сводится к обыкновенному дифференциальному уравнению второго порядка с постоянными коэффициентами с помощью подстановки: Ё = /r. Продифференцируем один и два раза это равенство для того, чтобы подставить результат в (3.23) и получить уравнение для .

После подстановки полученных выражений в (3.23) все слагаемые, содержащие первую производную, сократятся и уравнение примет стандартный вид:

Здесь частные производные заменены общими, поскольку — функция одной переменной.

Запишем решение уравнения в виде суммы двух экспонент, а затем вместо подставим его выражение через Ё .

Второе слагаемое описывает волну, перемещающуюся из бесконечности в начало координат. Оно становится бесконечным при г = 0, поэтому его надо отбросить и считать В = 0. Окончательно для электрического поля в сферической волне получим.

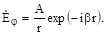
(3.24).

Если в цилиндрической системе координат плотность энергии была обратно пропорциональна расстоянию от оси z, а электрическое поле — обратно пропорционально корню из этого расстояния, то в сферической системе плотность энергии обратно пропорциональна квадрату расстояния от начала координат (площадь сферы равна 4г²), а амплитуда электрического поля обратно пропорциональна радиусу.

Рассчитаем комплексную амплитуду магнитного поля, воспользовавшись первым уравнением (2.1.4) с нулевой плотностью магнитного тока.

(3.25).

Запишем его в сферической системе координат. Чтобы сократить запись, учтем, что у электрического поля есть единственная проекция — и зависит она от единственной координаты г. В сложном выражении для ротора векторного поля в сферической системе координат отличная от нуля производная входит во второе слагаемое проекции ротора на ось (смотри приложение). Поэтому в левой части (3.25) оставим только это слагаемое, а в правой проекцию напряженности магнитного поля на ось. Подставим выражение для Ё и найдем магнитное поле:

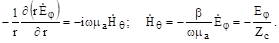
(3.26).

Если систему координат выбрать так, что электрическое поле направлено по оси И, то связь и осталась бы прежней с точностью до знака.

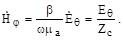
В отличие от цилиндрических волн, у сферических связь между и точно, а не приближенно та же, что и для плоских волн. Это связано с характером изменения координат z и ц в цилиндрической и ц и и в сферической системе координат. Для цилиндрической координата z изменяется по прямой линии — образующей цилиндра, а ц — по кривойокружности с = const. Характер изменения координат различный, что и приводит к изменению отношения _z к. В сферической же системе и ц и и изменяются по окружности и связь между и та же, что и в плоских волнах. Впрочем, на достаточно большом удалении от начала координат вблизи точки наблюдения и сферу, и цилиндр можно приближенно представить в виде плоскости. Таким образом, основной вид электромагнитных волн — плоские волны.