Примеры решения задач

Пример 5.1. Рассчитаем на прочность и подберем размеры поперечного сечения для консольного стержня (рис. 5.23, а). Материал стержня — малоуглеродистая сталь. Дано: F = 10 кН; / - 1,2 м; сг_т = 300 МПа; [и_т] - 2.

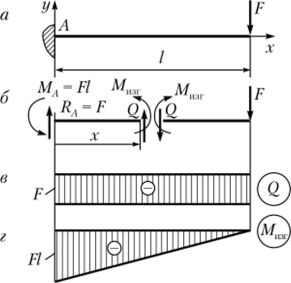
Рис. 5.23. К примеру 5.1.

Решение. Составим уравнения равновесия и определим реакции в заделке А:

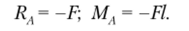
В правосторонней системе координат рассмотрим сечение стержня с текущей координатой х. В левом береге сечения (рис. 5.23, б), нормаль к которому совпадает с положительным направлением оси х, положительные направления перерезывающей силы О = Q и изгибающего момента М_г = М_тг совпадают с положительными направлениями системы координат. Рассматривая условия равновесия отсеченной левой части стержня, находим:

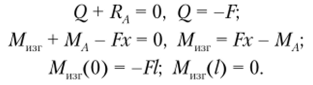
Эпюры поперечной силы и изгибающего момента показаны па рис. 5.23, в, г. Поперечная сила в стержне постоянна. Изгибающий момент изменяется по линейному закону. Опасным является закрепленное сечение — заделка. Максимальный по абсолютному значению момент в заделке равен FI.

В соответствии с методом расчета по допускаемым напряжениям составим условие прочности:

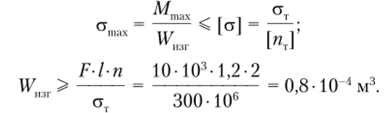
Рассмотрим три вида поперечных сечений (рис. 5.24).

Для кругового поперечного сечения (рис. 5.24, а) получим.

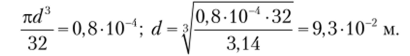
Площадь круглого сечения составит.

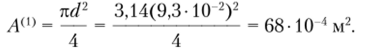
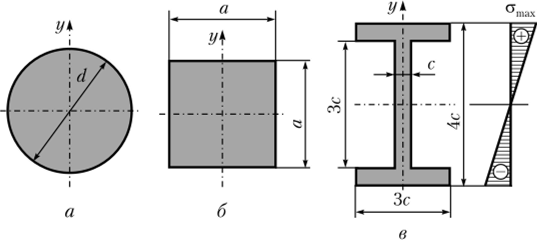
Рис. 5.24. Поперечные сечения к примеру 5.1

Момент сопротивления изгибу и допустимый размер для квадратного сечения будут соответственно равны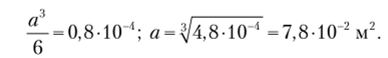

Площадь квадратного сечения будет равна Л⁽²⁾ = а² = 61,3−10 ⁴ м².

Для определения значения центрального осевого момента инерции двутаврового сечения используем формулу (3.28):

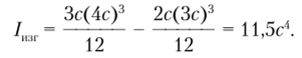
Значение центрального осевого момента сопротивления для этого сечения составит.

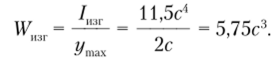
Определим размер сечения с и его площадь:

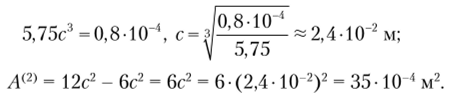
Анализируя полученные результаты, убеждаемся в том, что использование двутаврового сечения приводит к существенной экономии материала. Вычислим коэффициенты эффективности применения кругового и квадратного сечений относительно двутаврового сечения (табл. 5.2).

Таблица 5.2

Сравнение эффективности использования материала для различных сечений

Таким образом, по сравнению с двутавровым сечением применение кругового сечения приводит к перерасходу материала на 97%, а в случае прямоугольного сечения этот показатель равен 77%.

Пример 5.2. Рассчитаем на прочность стержень, нагруженный распределенной нагрузкой постоянной интенсивности (рис. 5.25, а). Поперечное сечение стержня — прямоугольное (рис. 5.25, б). Дано: с/ = 10 Н/м; / = 1,2 м; сг_т = 400 МПа; [и_т] = 2.

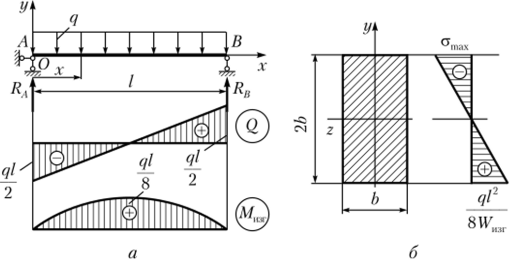
Рис. 5.25. К примеру 5.2.

Решение. Составим уравнение равновесия сил на вертикальную ось и уравнение моментов относительно точки О:

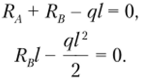
Решая систему, находим.

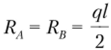
Используем метод сечений (рис. 5.26) и составим уравнение равновесия для отсеченной левой части стержня:

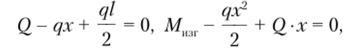
откуда получим выражения для поперечной силы и изгибающего момента:

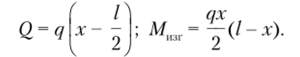
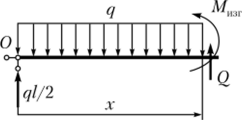
Рис. 5.26. Метод сечений к решению примера 5.2

Таким образом, поперечная сила изменяется, но линейному закону, а изгибающий момент представлен квадратной параболой. Закон изменения силовых факторов соответствует дифференциальным и интегральным зависимостям (5.1)—(5.3).

Установим значения поперечной силы и изгибающего момента в характерных сечениях стержня:

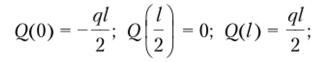
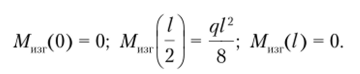
Эпюры поперечной силы и изгибающего момента представлены на рис. 5.25, а. С помощью второй эпюры устанавливаем, что опасным является среднее сечение х- ½. Эпюра нормальных напряжений представлена на рис. 5.25, 6. Составим условие прочности для определения размеров сечения:

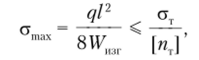
откуда получим значение осевого момента сопротивления:

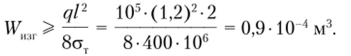
Зная значение осевого момента сопротивления, определим минимально допустимое значение для ширины сечения:

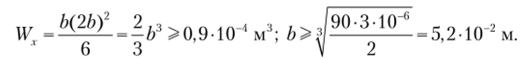
Пример 5.3. Рассчитаем чугунный стержень (рис. 5.27) на прочность и определим размеры его сечения. Дано: о = 150 МПа; а_|1(. = 600 МПа; / = 1 м; F = 20 кН;

[п J = 2.

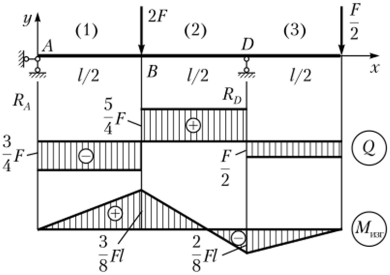
Рис. 5.27. К примеру 5.3.

Определим силы реакции. Для этого составим уравнение суммы моментов всех сил, приложенных к стержню, относительно точки А и уравнение равновесия на ось у:

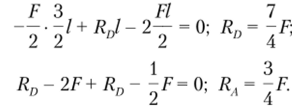
Точки приложения сил делят стержень на три участка.

С помощью метода сечений рассмотрим первый участок 0 < д⁴⁰ < ½ (рис. 5.28, а). Используя уравнения равновесия первого участка стержня, определим соответствующие ему значения поперечной силы и изгибающего момента:

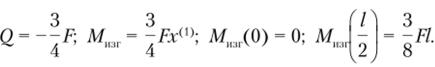
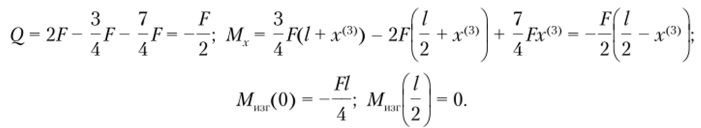aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">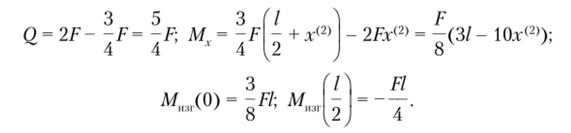

Сохраняя преемственность, аналогично второму рассмотрим и третий участок О < х < ½ (рис. 5.28, в):

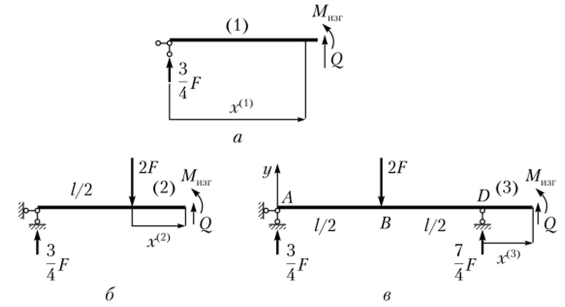
Рис. 5.28. Участки к решению примера 5.3.

Аналогично рассмотрим второй участок системы 0 < х⁽²⁾ < ½ (рис. 5.28, б):

Отметим, что расчет третьего участка системы можно было осуществить рассмотрением отсеченного участка с правой стороны стержня:

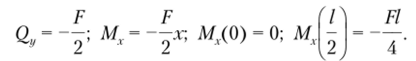
По результатам расчетов построим эпюры поперечных сил и изгибающих моментов (см. рис. 5.27).

Определим геометрические характеристики сечения (рис. 5.29, а).

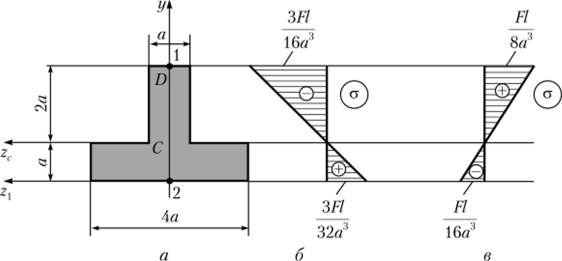
Рис. 5.29. Сечение и эпюры нормальных напряжений к решению примера 5.3.

Для установления ординаты его центра тяжести в качестве начальной возьмем ось г, и используем формулу (3.7):

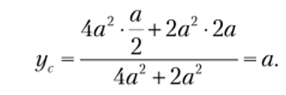
Для определения осевого момента инерции сечения представим его как два прямоугольника, определим их осевые моменты инерции раздельно относительно центральной оси всей фигуры по формуле (3.27), а далее искомую величину определим сложением характеристик составляющих фигур: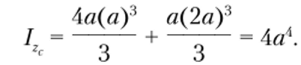

Свойства материала на растяжение и сжатие различаются и к тому же сечение несимметрично относительно центральной оси. Анализ эпюр изгибающих моментов показывает, что опасными могут быть сечения В и D (см. рис. 5.27). В первом сечении в точках, наиболее удаленных от центральной оси, нормальные напряжения будут.

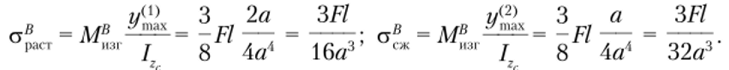
Для течения В эпюра нормальных напряжений представлена на рис. 5.29, б. Аналогично определим напряжения в сечении D:

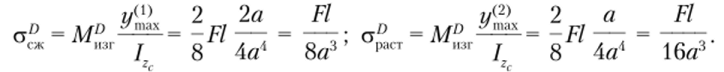
Для этого сечения эпюра нормальных напряжений представлена на рис. 5.29, в. Но данным построенных эпюр устанавливаем, что максимальное растягивающее напряжение действует в точке 1 второго сечения D. Сформулируем для этой точки условие прочности:

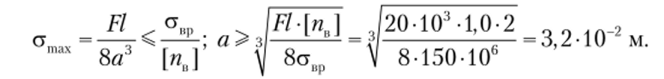
Наибольшее по модулю сжимающее напряжение действует в точке 1 сечения В. Условие прочности запишется в следующем виде:

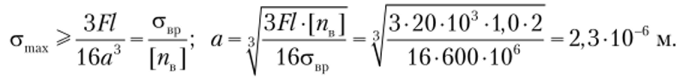
Таким образом, выполнение условия прочности на растяжение требует больших размеров сечения, чем было получено из условия выполнения прочности на сжатие. Поэтому окончательно следует взять а > 3,2 см. Таким образом, опасным является сечение D, опасными являются точки, удаленные от центральной оси z_c на расстояние 2а. Отметим, что если изменить ориентацию сечения и поместить полку сверху, то в результате расчета получим а > 3,7 см.

Пример 5.4. Рассчитаем на прочность раму, представленную на рис. 5.30, а. Используя метод расчета по допускаемым напряжениям, определим размеры прямоугольного поперечного сечения. Высота сечения в два раза больше его ширины. Дано: / = 0,5 м; F = 40 кП; а_тр = а_тс = а_т = 450 МПа; [п_т] = 2.

Решение. Построим для рамы эпюры нормальных сил, поперечных сил и изгибающих моментов.

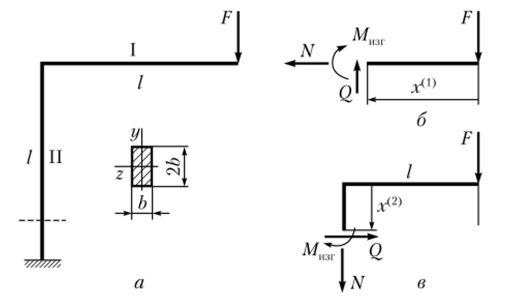
Puc. 530. К примеру 5.4.

Воспользуемся методом сечений и запишем условия равновесия для первого участка 0 < х⁽¹⁾ < / (рис. 5.30, б)

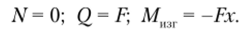
Рассмотрев второй участок 0 < х⁽²⁾ < / (рис. 5.30, в) и записав для него условия равновесия, получим значения внутренних силовых факторов для второго участка:

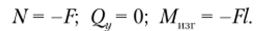
Результаты расчета представлены в виде эпюр на рис. 5.31. При построении эпюры изгибающих моментов целесообразно придерживаться следующего правила: данная эпюра строится со стороны сжатых волокон^[1]. Что же касается эпюр нормальных и перерезывающих сил, то здесь определенных правил не придерживаются.

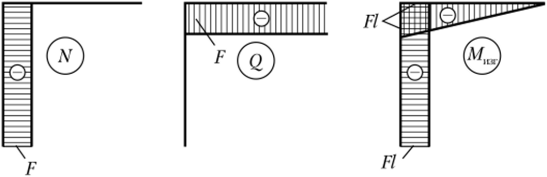
Рис. 531. Эпюры к примеру 5.4.

В качестве опасного можно рассматривать любое сечение второго участка, так как в нем одновременно с максимальным значением изгибающего момента действует также нормальная сила. Вызванные в сечении от нормальной силы напряжения равномерно распределены в сечении и определяются формулой (2.3):

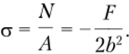
Что касается напряжений, вызванных изгибающим моментом, то они изменяются по линейному закону и определяются по формуле (5.10):

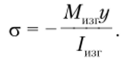
Эпюры нормальных напряжений в опасном сечении представлены на рис. 5.32.

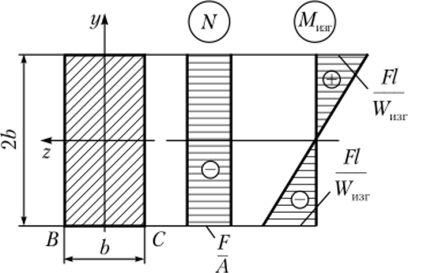
Рис. 5.32. Эпюры нормальных напряжений в опасном сечении к примеру 5.4

Непосредственно в самом сечении опасной является любая точка на стороне сечения ВС, в которой общее нормальное напряжение представляет собой сумму напряжений от сжатия и изгиба. Поскольку напряжение является сжимающим, приведем его значение по модулю:

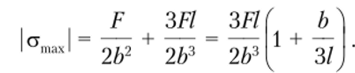
При рассмотрении рам, состоящих из стержневых элементов, продольные размеры которых значительно больше размеров поперечных сечений (b/l= 1), можно пренебречь малыми величинами и переписать формулу для максимального напряжения в виде.

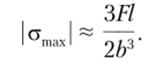
Как правило, при расчете рам по причине малости можно пренебречь вкладом в напряженное состояние, вызванным действием нормальных сил, по сравнению с напряжениями от изгиба. Приведенные в параграфе 5.5 оценки относительной величины напряжений, обусловленных поперечной и нормальной силами, по сравнению с напряжениями от изгибающих моментов для прямолинейных стержней остаются в силе и для рам.

Условие прочности запишется в следующем виде: 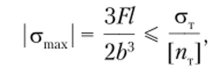откуда найдем размер поперечного сечения:

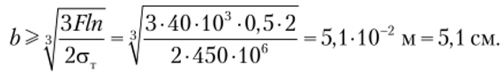
Определим размеры сечения по методу предельной нагрузки. Используем то же самое значение коэффициента запаса, [n_L = 2. Условие прочности запишем в следующем виде:

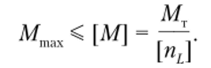
Если в это условие подставить значение предельного момента для сечения M_L, которое определим по формуле (5.49), то получим.

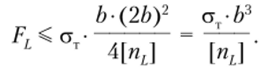
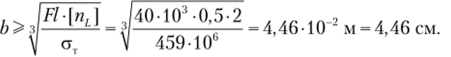
Сравним веса рам, определенные по методам допускаемых напряжений и предельных нагрузок, которые пропорциональны квадрату размера поперечного сечения Ь:

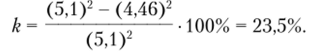
Таким образом, в случае расчета по методу допускаемых напряжений размеры сечения рамы получаются больше, чем при расчете по методу предельных нагрузок. Формально перерасход материала составляет 23,5%.

Пример 5.5. Рассчитаем на прочность раму (рис. 5.33). Стержни рамы имеют круговые поперечные сечения. Установим размер поперечных сечений d. Дано: F = = 10 кН; / = 0,5 м; ст_ф = сг_тс = 450 МПа; [и_т] = 2.

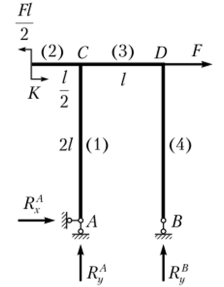
Рис. 5.33. К примеру 5.5.

Решение. Определим реакции в опорах. Используя уравнение моментов относительно точки А, найдем реакцию в опоре В: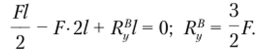

Используя уравнения равновесия в горизонтальном и вертикальном направлениях, найдем.

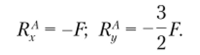
Рассмотрим первый участок рамы 0 < х^(|> < 21 (рис. 5.34, а) и с помощью уравнений равновесия определим в нем внутренние силовые факторы:

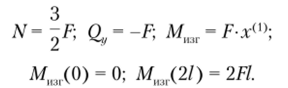
Аналогично рассмотрим и второй участок 0 < х⁽²⁾ < ½ (рис. 5.34, б):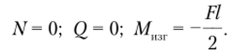

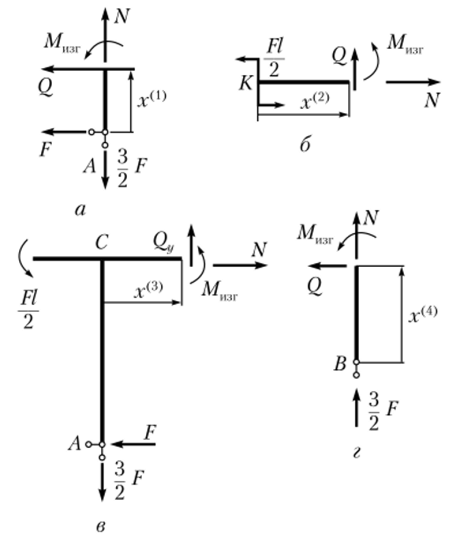
Рис. 5.54. Участки к решению примера 5.5

Для третьего участка 0 < х⁽³⁾ < / с использованием метода сечений (рис. 5.34, в) определяем в его сечении внутренние силовые факторы:

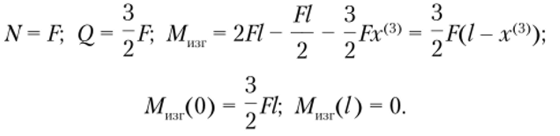
Используя метод сечений, для четвертого участка 0 < х⁽⁴⁾ < 2/ (рис. 5.34, г) находим: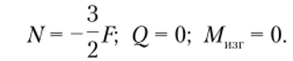

Используя полученные результаты, построим эпюры внутренних силовых факторов рамы (рис. 5.35).

На основе эпюры изгибающих моментов устанавливаем, что опасным является сечение С на первом участке, для которого условие прочности запишется в виде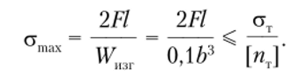

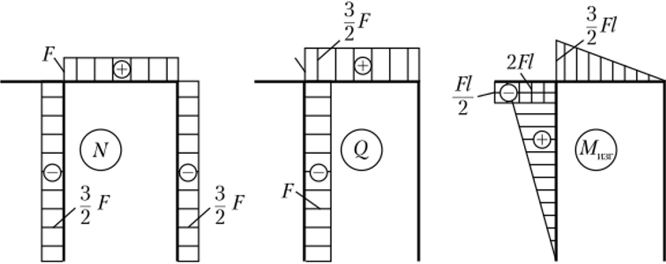
Рис. 5.35. Эпюры внутренних силовых факторов рамы к примеру 5.5

Считаем, что для материала рамы допустимо описание по схеме идеального упругопластичного материала. Проведем расчет рамы на прочность по методу предельной нагрузки, приняв [и,] = 2:

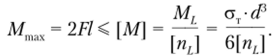
Определим диаметр сечения по методу предельной нагрузки:

Пример 5.6. Рассчитаем на прочность по методу допускаемых напряжений брус с круговым поперечным сечением (рис. 5.36) и установим размеры сечения. Дано: F- 10 кН; [о] = 160 МПа.

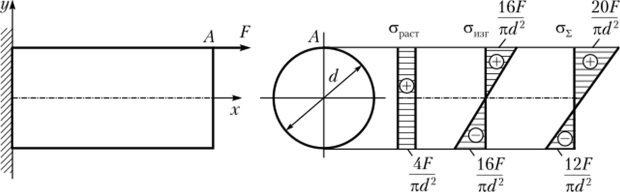
Рис. 5.36. К примеру 5.6.

Решение. Стержень находится в условиях внецентренного растяжения. В любом его сечении действует нормальная растягивающая сила N — F; изгибающий момент Fd

М_1ИГ= ——. Определим соответствующие им нормальные напряжения:

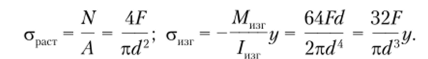
Эпюры напряжений от растяжения и изгиба, а также суммарная эпюра напряжений представлены на рис. 5.36. Для опасной точки А условие прочности запишем в следующем виде:

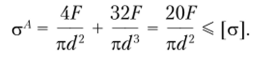
Используя условие прочности, определим допустимый диаметр стержня:

Пример 5.7. Определим, но методу допускаемых напряжений размеры стержня с прямоугольным поперечным сечением (рис. 5.37). Дано: F = 65 кН; |а | = 200 МПа.

Решение. Стержень подвергается внецентренному сжатию, и для его расчета можем использовать формулы, приведенные в параграфе 5.8. Но в данном случае решение может быть получено более просто, основываясь на физическом смысле задачи.

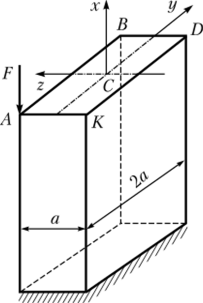
Рис. 5.37. К примеру 5.7

Установим значения нормальной силы и изгибающих моментов в поперечных сечениях стержня: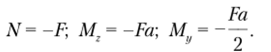

Знаки моментов соответствуют правилам для правосторонней декартовой системы координат. Подсчитаем раздельно напряжения от нормальной силы и изгибающих моментов:

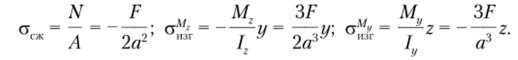
Эпюры, соответствующие нормальным напряжениям, представлены на рис. 5.38.

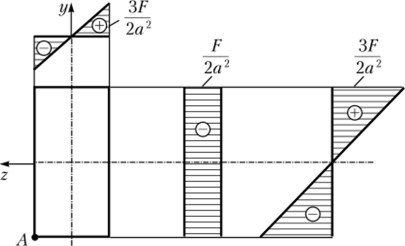
Рис. 5.38. Эпюры, соответствующие нормальным напряжениям, к примеру 5.7

В соответствии с полученными результатами опасной является точка Л, в которой суммарное значение всех трех нормальных напряжений составит.

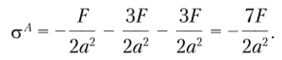
Составим условие прочности и определим минимально допустимый размер сечения:

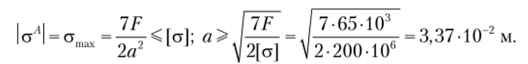
Пример 5.8. Сравним по метолу допускаемых напряжений прочность двух одинаково нагруженных стержней, поперечное сечение которых ослаблено односторонним и двухсторонним вырезами соответственно (рис. 5.39).

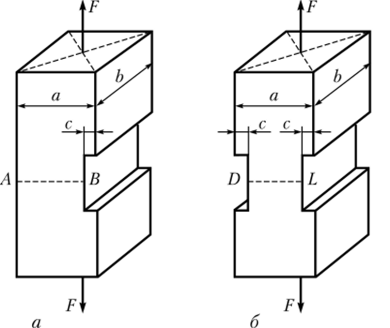
Рис. 5.39. К примеру 5.8.

Решете. Рассмотрим первый стержень (рис. 5.39, а), для которого в опасной точке В сечения А В имеет место внсцснтрсннос растяжение и полное напряжение равно.

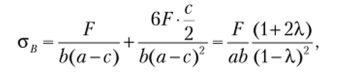
где X = с/а.

Для второго стержня опасным является сечение DL, находящееся в условиях центрального растяжения, в любой точке которого напряжение равно.

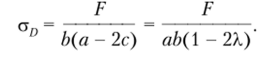
Определим отношение максимальных значений напряжений в опасных точках первого и второго стержней:

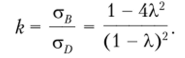
Построим график, характеризующий зависимость коэффициента к от геометрического параметра X (рис. 5.40).

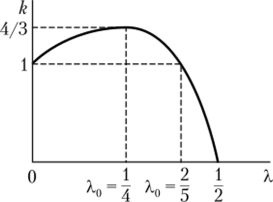
Рис. 5АО. График зависимости коэффициента k от параметра X.

При А, — 0, т. е. в случае отсутствия вырезов, к = 1, и с точки зрения прочности оба стержня равнозначны.

Проверим, существует ли другое решение, соответствующее равнопрочным стержням. Для этого приравняем выражение для k единице и решим полученное квадратное уравнение относительно неизвестных геометрических параметров:

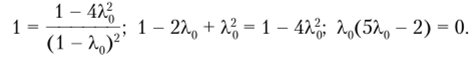
Одно нулевое решение этого уравнения мы уже получили. Второе получим, приравняв к нулю второй сомножитель:

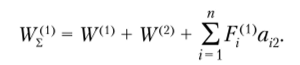
Отсюда следует второе значение геометрического параметра а.,.

Определим значение X*, соответствующее значению к, при котором отношение прочности первого стержня максимально превосходит прочность второго стержня. Продифференцировав выражение для к по X и приравняв результат к нулю, найдем координаты экстремумов:

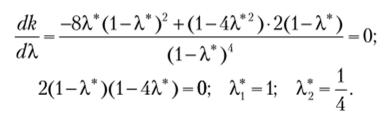
Первый корень выходит за границы изменения, так как X может меняться только в пределах 0 < X < 0,5 (см. рис. 5.40). Второму корню соответствует максимальное значение к

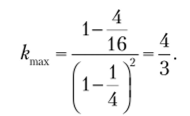
п к.

Интересен тот факт, что при значениях 0 < X < X F/^{1 )}а_а = X F/²⁾«., второй, «ос;

1=1 j-1

лаблепный" лишним вырезом стержень оказывается более прочным.

Пример 5.9. Проведем поверочный расчет консольного стержня с L-образным поперечным сечением (рис. 5.41) на прочность. По методу допускаемых напряжений определим размеры поперечного сечения. Дано: F= 5 кН; I = 1,5 м; ст_г = 450 МПа;

К] - 3.

Максимальный изгибающий момент М = FI возникает в заделке стержня. Сечение L-образной формы было рассмотрено в примере 3.6. При этом были установлены положение главных центральных осей и значения главных осевых моментов инерции:

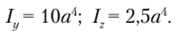
Поскольку силовая линия не совпадает ни с одной из главных осей сечения (рис. 5.42), стержень находится в условиях косого изгиба.

Силовая линия совпадает с осью Oz, и составляет с осью Оу угол.

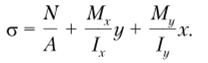
Рис. 5.41. К примеру 5.9

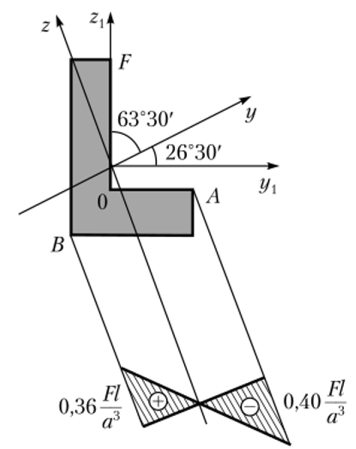
Рис. 5.42. Силовая линия к решению примера 5.9

Поэтому в соответствии с соотношением (5.65) формула для нормальных напряжений от изгиба запишется в следующем виде:

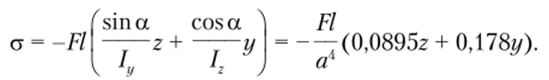
В соответствии с формулой (5.66) определим уравнение нейтральной оси:

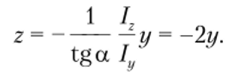
Из двух точек А и В опасной является та, которая максимально отдалена от нейтральной линии. Координаты точек следующие: А ( 1,12а; 2,24а); В (- 1,56а; -0,90а). Определим в этих точках значения нормальных напряжений:

Из полученных результатов очевидно, что опасной является точка Л. Используя условие прочности, определим характерный размер сечения а:

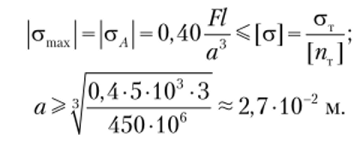
• [1] В учебниках для строительных специальностей придерживаются противоположногоправила — эпюра строится со стороны растянутых волокон.