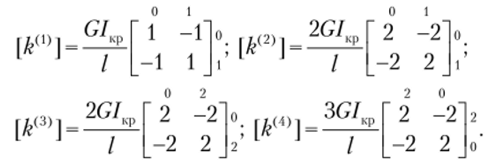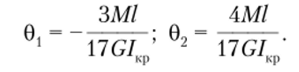Пример 9.1. Используя метод прямых жесткостей, получим матрицу жесткости трехузлового одномерного конечного элемента, работающего на растяжение-сжатие (рис. 9.16, а).
Решение. В соответствии с прямым методом жесткостей проведем три вспомогательных теста. При проведении первого теста вычислим узловые усилия, вызванные единичным смещением узла 1 в положительном направлении при запрещении перемещений узлов 2 и 3 (рис. 9.16, 6). Находим.
Аналогичным образом проведем тест номер 2 (рис. 9.16, в). Получим 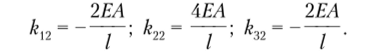

aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">

Рис. 9.16. К примеру 9.1
Определение компонентов матрицы к завершим тестом номер 3 (рис. 9.16, г):
Окончательно матрица жесткости одномерного трехузлового конечного элемента, работающего на растяжение-сжатие, запишется в виде.
Пример 9.2. Определим углы поворота и величину внутренних крутящих моментов для составного вала (рис. 9.17). Участки 1 и 2 вала помещены в трубку 3 и абсолютно жестко соединены с участком 4. Дано: G; /,.р; /; М.
Решение. В качестве элементов рассмотрим отдельные участки вала. Конструкция содержит четыре элемента и четыре узла. При глобальной нумерации присвоим узлам, в которых запрещены перемещения, номер 0. Таким образом, конструк;

Рис. 9.17. К примеру 9.2.
ция содержит только два угловых перемещения 0, и 02, подлежащих определению. Глобальная матрица жесткости будет иметь размерность 2×2.
Составим матрицу соответствия индексов:
Номер элемента е | Глобальный индекс соответствующий локальному индексу 1. | Глобальный индекс j, соответствующий локальному индексу 2. |
| | |
| | |
| | |
| | |
Согласно формулам (9.11), (9.12) выпишем матрицы жесткости элементов и произведем их индексное окаймление:
Проведем сборку глобально матрицы жесткости ансамбля конечных элементов. Компоненты, стоящие в локальных позициях, которым соответствует нулевой глобальный номер строки или столбца, в сборке нс участвуют:
Вектор узловых перемещений и вектор узловых сил будут иметь следующий вид:
Запишем систему алгебраических уравнений для ансамбля конечных элементов:
Решая систему, находим.
Подсчитаем величины крутящих моментов в элементах системы:
В качестве проверки рассмотрим равновесие узла 2 (рис. 9.18).

Рис. 9.18. Равновесие узла 2 к примеру 9.2.


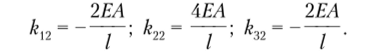
 aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">
aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">