Основы дисперсионного анализа

Различия между значениями отдельных элементов статистической совокупности складываются под влиянием множества отдельных факторов. Степень влияния факторов на изменение величины признака неодинакова. Одни факторы в большей степени, а другие — в меньшей степени оказывают влияние на вариацию признака. Поэтому различают вариации систематическую и случайную. Задача дисперсионного анализа заключается в исследовании влияния тех или иных факторов на изменчивость средних значений изучаемого признака. С этой целью производится разложение дисперсии наблюдаемой совокупности на составляющие, порождаемые независимыми факторами. Общая дисперсия раскладывается на факторную (межгрупповую) дисперсию, связанную с груииировочным признаком, и остаточную (внутригрупповую) дисперсию, не связанную с группировочным признаком. Факторная дисперсия объясняет вариацик) результативного признака под влиянием изучаемого фактора; остаточная дисперсия — вариацию результативного признака, обусловленную влиянием прочих факторов (за исключением влияния изучаемого фактора). Сущность дисперсионного анализа заключается в сопоставлении межгрупповой и внутригрупповой дисперсий и формировании на основе этого соотношения суждения о влиянии и роли изучаемого фактора.

В дисперсионном анализе дисперсией называют сумму квадратов отклонений индивидуальных значений признака от их средней арифметической. Сначала определяют общую дисперсию, обусловленную влиянием вариации всех признаков, затем факторную и остаточную дисперсии.

Определение общей дисперсии, обусловленной влиянием на вариацию у всех признаков, производится по формуле.

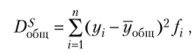
где г/; — отдельные значения результативного признака; у_{о (т} — общая средняя; J — число единиц совокупности в каждой группе.

Факторная дисперсия представляет собой сумму квадратов отклонений частных (групповых) средних от общей средней, умноженных на число единиц в каждой группе:

где у_гр — групповые средние значения результативного признака; у_общ — общая средняя; f — число единиц совокупности в каждой группе.

Остаточная дисперсия (случайная) есть сумма групповых сумм квадратов отклонений всех вариант результативного признака в группах от средних значений признака в них:

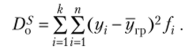
Далее производится оценка достоверности влияния факторного признака на результативный. Для этого определяется число степеней свободы вариации г. Различают степени свободы факторной и остаточной дисперсий. Число степеней свободы для факторной дисперсии равно количеству групп минус единица. Эта величина показывает, что в такой выборочной совокупности (любая выборка имеет ограниченный объем) каждая варианта свободна принимать любые значения, кроме одного, определяемого разностью между суммой всех остальных вариант и объемом выборки, т. е. одна варианта не имеет степени свободы вариации. Если выборочная совокупность достаточно велика, то разница между N и N — 1 несущественна, поэтому не оказывает влияния на результат расчетов. Число степеней свободы для остаточной дисперсии равно разности между количеством индивидуальных значений признака и числом групп.

Затем рассчитываются дисперсии на одну степень свободы вариации (такая дисперсия может быть обозначена как D*). В этом случае дисперсии выступают как показатели, позволяющие сравнивать группы с разной численностью. Далее осуществляется проверка правильности расчетов числа степеней свободы вариации.

Отношение факторной и остаточной дисперсий, рассчитанных на одну степень свободы, позволяет определить критерий Фишера (Е-критерий):

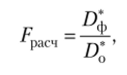
где Ц], — факторная дисперсия на одну степень свободы; D* — остаточная дисперсия на одну степень свободы.

Р. Фишером было установлено распределение отношений дисперсий, а также разработаны специальные таблицы теоретических значений Е-критерия при двух вероятностях: 0,05 и 0,01. Находят теоретическое значение Е-критерия по таблицам для принятого в исследовании уровня значимости с учетом числа степеней свободы для факторной и остаточной дисперсий. При этом 5%-ному уровню значимости соответствует 95%-ный уровень вероятности, 1%-ному — 99%-ный уровень вероятности. В большинстве случаев избирают 5%-ный уровень значимости. Теоретическое значение Е-критерия при заданном уровне значимости по таблицам определяют на пересечении строки и столбца, соответствующих двум степеням свободы дисперсий: по строке — остаточной, но столбцу — факторной.

Расчетное значение F-критерия сравнивают с табличным:

если F_paC4 > F_Taбл, то статистическое наблюдение доказывает с вероятностью, большей заданной, влияние фактора на результативный признак;

если F_pac4 = F_Ta6l, то статистическое наблюдение доказывает с заданной вероятностью влияние фактора на результативный признак;

если F_paC4 < F_ra6ri, влияние фактора на результативный признак не доказано, но не доказано и отсутствие влияния фактора. Статистическое наблюдение необходимо повторить, уравнивая группы по факторам, за исключением изучаемого фактора, или увеличить количество единиц изучаемой совокупности;

если F_paC4":F_ra5_ri (т.е. F_pac4 много меньше F_Ta6t]), то рассчитывают F_paC4 как отношение остаточной дисперсии на одну степень свободы к факторной дисперсии на одну степень свободы:

Теоретическое значение^{-критерия} в данном случае определяют при заданном уровне значимости, но таблицам на пересечении строки и столбца, соответствующих двум степеням свободы дисперсий: по строке — факторной, по столбцу — остаточной. Если Е_р*_асч > F_T*_aбл, то статистическое наблюдение достоверно доказывает отсутствие влияния фактора на результативный признак.