Решение задач пространственной статики

При выполнении расчетов вместо векторных равенств (3.3), (3.4) используют их проекции на оси координат с началом в моментной точке О.

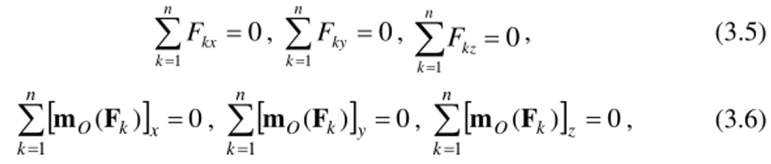
Эти шесть уравнений, очевидно, равносильны условиям (3.3) — (3.4).

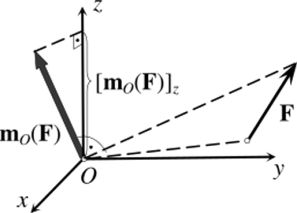
Рис. 3.12.

Обратим внимание на проекции векторных моментов, входящие в равенства (3.6). Для вычисления каждой из них требуется сначала найти векторный момент силы m₀(F), а затем спроецировать его на соответствующую ось (рис. 3.12).

Покажем, что этим проекциям можно дать простое физическое истолкование, а заодно и получить удобное правило их вычисления. Для этого рассмотрим новую величину — момент силы относительно оси.

Определение 4. Момент силы F относительно оси s — это число m_v(F), равное по модулю моменту проекции F// силы F на плоскость Я, перпендикулярную оси s, относительно точки пересечения оси s и плоскости Я (рис. 3.13):

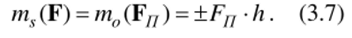
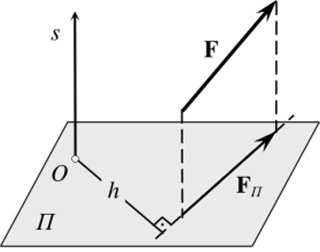
Рис. 3.13.

Знак m_s(F) положительный, если с конца оси s поворот вектора ?_п вокруг точки О видится происходящим против хода часовой стрелки, и отрицательный, если по ходу.

Нетрудно установить, что момент m_s (F) характеризует вращательное действие силы F на тело, для которого s является осью вращения.

мент силы относительно оси m_s

Кроме того, оказывается, что мо- (F) в точности равен проекции на эту ось векторного момента силы, т. е. m_s(F) = [m₀(F)]₉, где О — любая точка оси л Покажем справедливость последнего равенства.

На рис. 3.14 изображены: векторный момент m₀(F), его проекция на ось .9, а также проекция F^ силы F на плоскость Я, перпендикулярную оси л Рассмотрим два треугольника ОАВ и 0АВ. Т.к. s _1_ П, а вектор m₀(F) перпендикулярен плоскости ЬОАВ, то площади треугольников связаны соотношением.

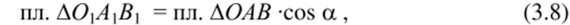
где, а — угол между осью s и вектором момента ш₀(?).

Эти же площади связаны с величинами моментов m_s(F) и ш_а(?):

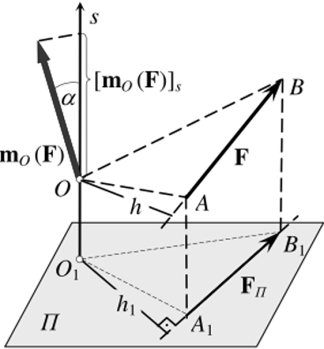
Рис. 3.14.

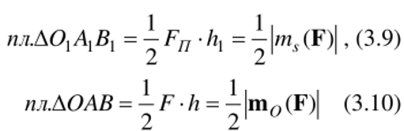
Сравнивая (3.8) и (3.9), (3.10), получаем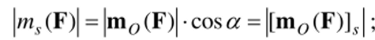

знаки момента m_s(F) и проекции [m₀(F)]₅, как видно из рис. 3.14, также совпадают, следовательно,.

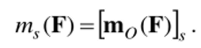
Последнее равенство позволяет записывать условия уравновешенности (3.5),(3.6) в следующем виде:

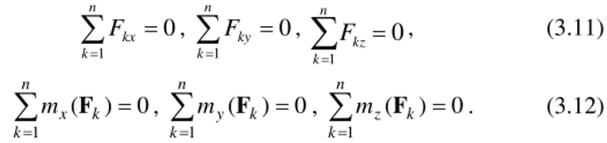
Таким образом, произвольная система сил {F_1? …, F"} уравновешена тогда и только тогда, если равны нулю суммы проекций всех сил системы на оси координат Ох, Оу, Oz , а также суммы моментов всех её сил относительно каждой из координатных осей.

Продемонстрируем использование условий уравновешенности (3.11), (3.12).

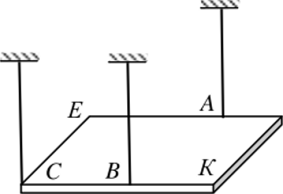
Рис. 3.15.

Пример 1. Прямоугольная однородная плита весом Q = 8 кН удерживается в горизонтальном положении тремя тросами (рис. 3.15). Размеры СК = 4 м, СЕ = = СВ = 2 м, ЕА = 3 м.

Найти натяжение каждого из них.

Решение. На плиту действуют сила тяжести Q и неизвестные реакции — натяжения тросов Ti, Т₂, Тз (рис. 3.16).

Выберем оси Ox, Оу, Oz так, как показано на рис. 3.16, и запишем условия уравновешенности (3.11)-(3.12) для системы сил Q, Т_ЬТ₂, Т₃: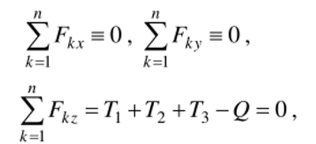

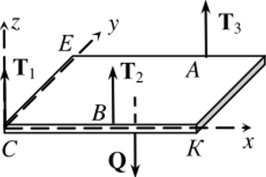
Рис. 3.16.

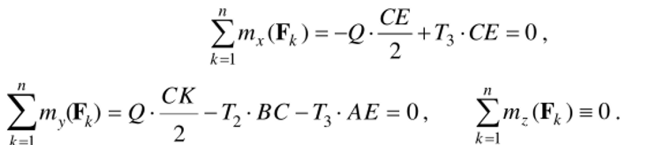
Решая полученные уравнения, находим: Г₃ = 0,5 (2 = 4 кН,.

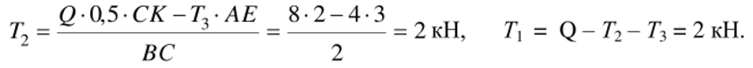
Задания для самостоятельной работы

• 1. Докажите, что модуль векторного момента силы равен удвоенной площади треугольника, одна из вершин которого — моментная точка, а две другие совпадают с началом и концом вектора силы.
• 2. Докажите, что векторный момент силы не изменится, если точку приложения силы перенести вдоль линии действия силы.
• 3. Докажите, что для уравновешенности произвольной системы параллельных сил {F|, …, F,} необходимо и достаточно выполнение следующих условий

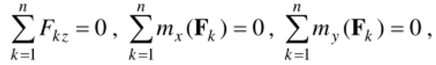
где ось z параллельна силам системы.

• 4. Покажите, что если сила и ось расположены в одной плоскости, то момент силы относительно этой оси равен нулю.
• 5. Попытайтесь обосновать следующее утверждение:

Момент m_s (F) характеризует вращательное действие силы F на тело, для которого s является осью вращения.