Примеры решения задач

Пример 13.1. Исследуем напряженно-деформированное состояние в круглой пластине радиуса R постоянной толщины А, нагруженной равномерно распределенной нагрузкой Контур пластины неподвижно защемлен (рис. 13.6). Определим величину объема, заключенного между начальной срединной плоскостью пластины и ее упругой поверхностью.

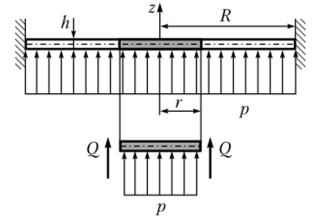
Рис. 13.6. К примеру 13.1.

Решение. Для определения величины Q рассмотрим равновесие центральной части пластины, вырезанной по окружности текущего радиуса:

откуда.

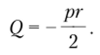
Из выражения (13.12) после двукратного интегрирования находим.

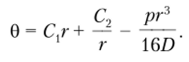
Поскольку угол поворота пластины и в центре (при г = 0) должен быть равен нулю, константа С₂ = 0. Таким образом, выражение для угла поворота приобретает вид.

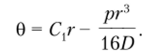
рг²

На контуре при г = R угол 0 = 0, откуда С, = и.

Согласно выражениям (13.6) получаем.

Используя выражения (13.17), получим формулы для определения напряжений в точках, расположенных у поверхности пластины (при z = ±h/2):

На рис. 13.7 показаны эпюры распределения напряжений по радиусу для точек, расположенных на верхней поверхности пластины.

Оценку прочностных характеристик пластины проведем, воспользовавшись энергетической теорией начала текучести. Учитывая, что напряженное состояние в пластине двухосное, эквивалентное напряжение а_экв в анализируемых опасных точках подсчитываем по формуле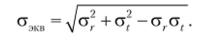

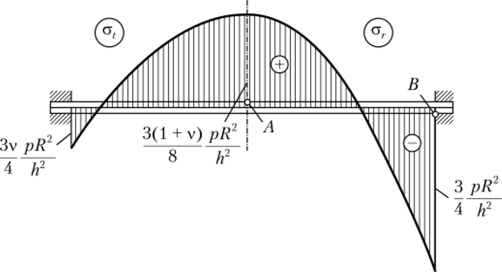
Рис. 13−7. Эпюры распределения напряжений по радиусу к примеру 13.1.

В центральной точке А, расположенной на верхней поверхности пластины, эквивалентное напряжение составит.

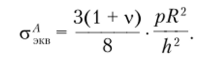
На краю пластины в точке В, расположенной на нижней поверхности пластины, напряжение равно.

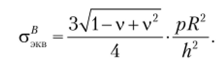
Принимая н = 0,3, находим.

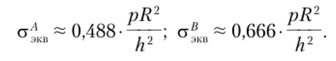
Таким образом, наиболее опасной точкой будет точка В у защемленного края на нижней поверхности пластины. Для оценки податливости пластины подсчитаем величину максимального прогиба. Согласно формуле (13.20).

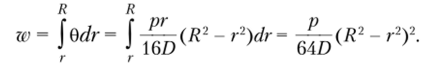
Максимальный прогиб возникает в центре пластины прн г= 0 и равен.

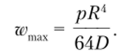
Определим величину объема, заключенного между срединной поверхностью в недеформированном состоянии и упругой поверхностью пластины.

Объем элементарного кольца равен (рис. 13.8) dV = 2лrdrw.

Рис. 13.8. К определению объема в примере 13.1.

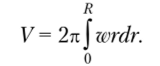
Используя выражение для максимального прогиба, получаем.

Пример 13.2. Кольцевая пластина, защемленная по контуру, усилена кольцевым ребром по внутреннему радиусу. Пластина нагружена по кольцу распределенной погонной нагрузкой F = 5 Н/мм. Материал пластины — сталь: модуль упругости Е = 2 • 10⁵ МПа; коэффициент Пуассона v = 0,3; предел текучести материала а_т = = 400 МПа; толщина пластины, А = 1 мм. Характерные размеры пластины: г, = 20А; г₂ = 40//; Н = ЗА; В=2А (рис. 13.9).

Рис. 13.9. К примеру 13.2.

Требуется определить коэффициент запаса по текучести и максимальный! прогиб пластины.

Решение. Рассматривая отсеченную текущим ралиусом г внутреннюю кольцевую часть пластины, находим.

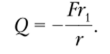
Используя правило взятия интеграла по частям, подсчитываем интеграл в формуле (13.12):

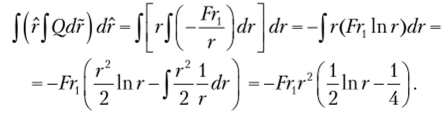
Общее решение дифференциального уравнения представим в виде.

Два последних слагаемых, равных в сумме нулю, добавлены для того, чтобы избавиться от размерной величины под логарифмом. Группируя слагаемые и вводя новую константу.

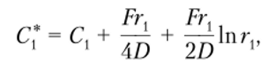
получаем зависимость для определения угла поворота 0:

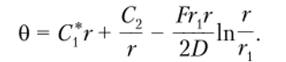
Дифференцируя, находим.

Изгибающие моменты равны.

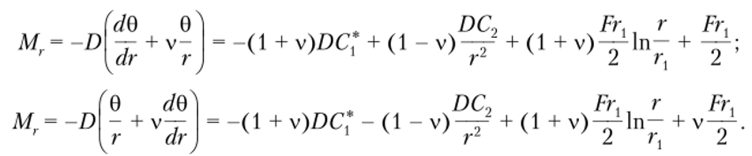
Граничные условия запишутся следующим образом.

1. При г = г, используем условие, описывающее сопряжения пластины с кольцевым ребром:

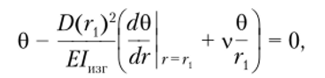
BW 2h (3 Hf.

nre/"_r— — — -4,5Й‘.

2. На внешнем контуре пластины при г = г₂ угол поворота равен нулю (0 = 0). При дальнейших расчетах удобно все линейные размеры выразить в долях толщины пластины /?. Вспомогательный множитель в граничном условии 1 для рассматриваемого случая запишется следующим образом:

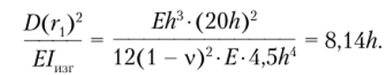
Подставляя выражения для угла поворота и его производной в граничные условия, получаем систему алгебраических уравнений.

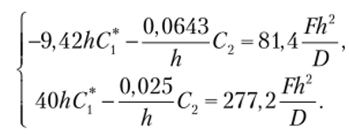
Решив эту систему, находим значения постоянных коэффициентов:

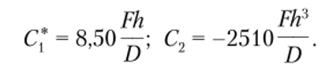
Искомая функция угла поворота имеет вид.

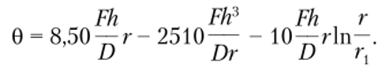
Выражения для изгибающих моментов запишутся следующим образом:

Эпюры распределения изгибающих моментов представлены на рис. 13.9. Наиболее опасными являются точки, расположенные на верхней поверхности у внешнего защемленного контура пластины, в которых возникают растягивающие напряжения от наибольшего по абсолютной величине момента M_r = 34,4F/z.

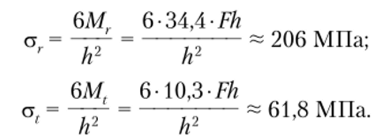
Эквивалентное напряжение по энергетической теории прочности составит 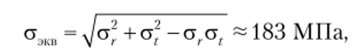а коэффициент запаса по текучести будет равен.

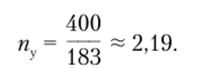
Максимальный прогиб, возникающий при г = г, подсчитаем по формуле (3.20), проинтегрировав функцию угла: