Лекция 12. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТЕОРЕМА МОМЕНТОВ

Как уже было отмечено (п. 10.4), два основных вида движения — поступательное и вращательное — несводимы друг к другу и являются в этом смысле элементарными движениями. В динамике это фундаментальное свойство движения проявляется в виде существования особой векторной меры вращательного движения — кинетического момента, или момента импульса. Для описания динамических свойств вращательной составляющей движения механической системы используется теорема об изменении кинетического момента.

Теорема об изменении кинетического момента

Рассмотрим движение механической системы, состоящей из п материальных точек с массами т_и т_п в инерциальной системе отсчета. Равнодействующую сил, приложенных к материальной точке массой ш, обозначим F,.

Продифференцируем по времени каждую часть равенства (10.4).

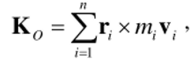
выражающего кинетический момент механической системы относительно неподвижной точки О:

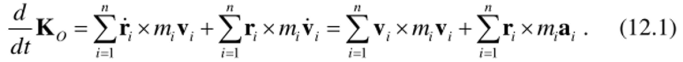
Первое слагаемое в правой части (12.1) равно нулю в силу известного свойства векторного произведения. Второе слагаемое преобразуем, используя основной закон динамики /Г7,а, = F, справедливый для каждой из точек системы:

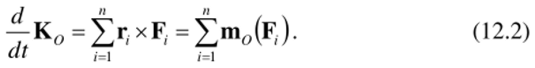
Представим вектор F, в виде суммы F, = F/^e) + F)^(,), где F/^и Б^⁽⁰— равнодействующие внешних и внутренних сил, приложенных к /-й точке. Тогда.

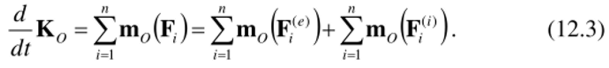
Силы взаимодействия любых двух точек системы равны по величине и противоположно направлены вдоль прямой, соединяющей эти точки. Поэтому сумма моментов всех внутренних сил системы равна нулю: ?т>‘")=0.

1=1.

В результате равенство (12.3) принимает следующий вид:

Полученное уравнение (12.4) выражает теорему об изменении кинетического момента механической системы:

Теорема. Производная по времени кинетического момента механической системы равна сумме моментов всех внешних сил этой системы (все моменты вычисляются относительно одного и того же центра, неподвижного в инерциальной системе отсчета).

Эту теорему часто называют также теоремой моментов, поскольку в обеих частях равенства (12.4) содержатся моменты: в левой — кинетический момент, в правой — моменты внешних сил.

Проецируя векторное равенство (21.4) на ось Os, проходящую через неподвижный центр О, получаем скалярную форму теоремы.

которую называют теоремой моментов относительно оси Os.

Векторное равенство (12.4) эквивалентно трем скалярным.

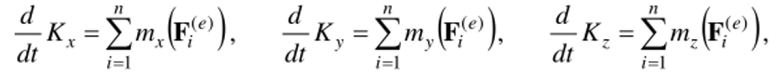
полученным его проецированием на декартовы оси с началом в точке О. Случай сохранения. Пусть на некотором промежутке времени.

[t_ut₂] выполняется условие ^m_oF-^e))=0, т. е. суммарный момент от;

i=1

носительно точки О всех внешних сил механической системы равен нулю. Тогда из теоремы (12.4) следует — К₀ = 0, при t_{ < t < и. Откуда.

dt

получаем К₍₎ = const, т. е. кинетический момент системы остается постоянным в течение промежутка времени [/_ь t₂].

Пример 1. Любопытно, что сформулированное выше правило сохранения кинетического момента явилось исторически первым обнаруженным в научных наблюдениях физическим законом сохранения.

В 1609 г. И. Кеплер опубликовал открытые им на основе астрономических наблюдений Т. Браге законы движения планет солнечной системы, в которых, в частности, установил, что секторная скорость^[1] движения планеты вокруг Солнца постоянна.

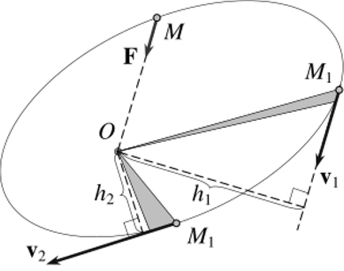
Рис. 12.1.

Сравним площади треугольников, «заметаемых» радиусом ОМ планеты за один и тот же малый промежуток времени At. Эти треугольники на рис. 12.1 выделены серым цветом. Для малого At можно считать, что одна из сторон каждого треугольника лежит на касательной к траектории и имеет длину vAt и v₂At соответственно. Высоты, проведенные к этим сторонам, перпендикулярны скоростям Vj и ₂ и имеют длины И и !ъ (рис. 12.1). Равенство площадей этих треугольников означает, что.

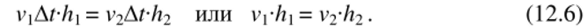
Проанализируем теперь движение планеты с точки зрения динамики. Будем считать планету материальной точкой, а с Солнцем свяжем инерциальную систему отсчета. Единственная сила, действующая на планету, — это гравитационная сила притяжения F, направленная к неподвижной точке О — центру масс Солнца. Момент этой силы nio (F) = 0, поэтому величина кинетического момента (10.13) планеты относительно точки О должна оставаться постоянной, т. е.

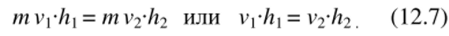
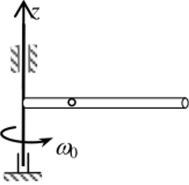
Рис. 12.2.

Совпадение (12.6) и (12.7) позволяет заключить, что равенство секторных скоростей планеты объясняется сохранением её кинетического момента.

Пример 2. В трубку, вращавшуюся вокруг вертикальной оси Oz с угловой скоростью помещают на расстоянии / от оси вращения шарик массой пг (рис. 12.2). Известны длина L трубки и её момент инерции I относительно оси вращения.

Найти угловую скорость трубки в момент вылета из неё этого шарика.

Решение. Рассмотрим движение механической системы, состоящей из трубки и шарика. Внешние силы этой системы: реакции N_b N₂ подшипников, силы тяжести трубки G и шарика mg. Как видно из рис. 12.3,.

J = 0. Поэтому из (12.5) следует —К. =0, т. е. кинетический /=i ' dt

Рис. 12.3.

момент этой механической системы относительно оси Oz сохраняет своё значение:

где to — начальный момент времени, когда шарик находился на расстоянии / от оси вращения; t — момент вылета шарика из трубки.

Кинетический момент К_: системы складывается из кинетического момента трубки и кинетического момента шарика. Кинетический момент трубки относительно оси вращения г вычисляем согласно (10.18):

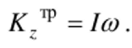
Кинетический момент шарика (материальной точки) вычисляем по правилам (10.10), (10.11), учитывая, что г х w (vi+v₂) = г х mv, + г х т₂:

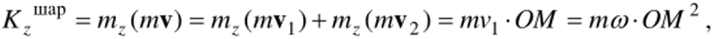
где mv, — продольная, mv₂ — поперечная составляющие импульса mv шарика (рис. 12.7).

Суммируя, получим.

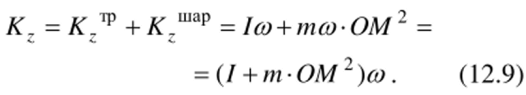aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">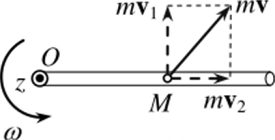

Рис. 12.7.

С учетом (12.9) равенство (12.8) принимает следующий вид:

где а> - угловая скорость трубки в момент вылета шарика. Из последнего равенства находим.

• [1] Секторная скорость — это площадь фигуры, которую «заметает» радиус планеты за единицу времени.