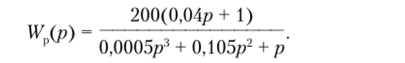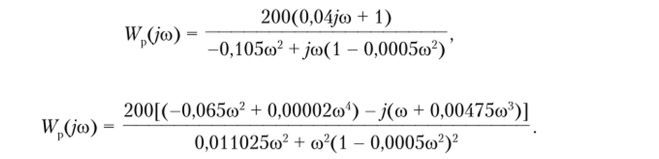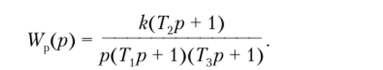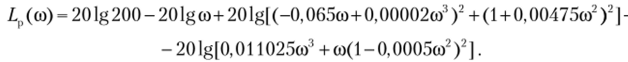Логарифмическая форма критерия Найквиста

Для проверки устойчивости замкнутой системы можно использовать логарифмические частотные характеристики разомкнутой, которые строятся почти без вычислений.

Формулировка критерия Найквиста: для устойчивости замкнутой системы необходимо и достаточно, чтобы на всех частотах, где Л, А ЧХ разомкнутой системы положительная (/-(со) > 0), фазовый сдвиг не достигал значения -180° или достигал его четное число раз (рис. 4.22).

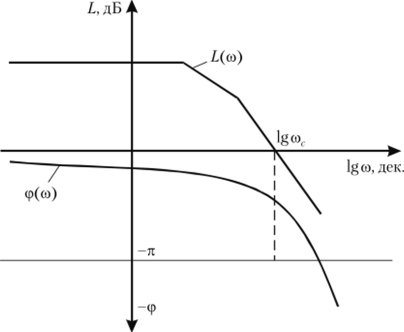
Рис. 4.22. Логарифмические частотные характеристики, иллюстрирующие критерий Найквиста Замкнутая система будет находиться на границе устойчивости, если на той же частоте со_г, где ЛАЧХ разомкнутой системы обращается в нуль (/.(со) = 0), фазовая частотная характеристика равна ср (со₍.) = -180°.

Пример 4.8. Проверить с помощью критерия Найквиста устойчивость системы фазовой автоподстройки частоты, упрощенная структурная схема которой приведена на рис. 4.23.

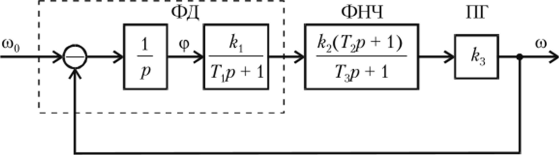
Рис. 4.23. Структурная схема системы фазовой автоподстройки частоты.

Здесь ПГ — подстраиваемый генератор, частоту которого (со) нужно стабилизировать; ФПЧ — фильтр нижних частот; ФД — фазовый детектор; со₀ — эталонная частота; (р — разность фаз эталонной частоты и частоты генератора. Параметры передаточных функций соответствующих устройств следующие: Г, = = 0,1 с; Т₂ = 0,04 с; Т₃ = 0,005 с; k = k_tk₂k₃ = 200 с ¹

Решение

Разорвем обратную связь и определим передаточную функцию разомкнутой системы:

Подставляя вместо параметров их числовые значения, получим 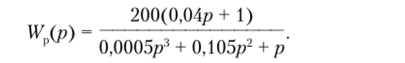Перейдем теперь к частотной характеристике заменой р —*jca:

Запишем теперь выражения для амплитудной частотной и фазовой частотной характеристик:

В логарифмическом масштабе амплитудная частотная характеристика име.

ет вид На рис. 4.24 представлены логарифмические амплитудная частотная и фазовая частотная характеристики разомкнутой системы.

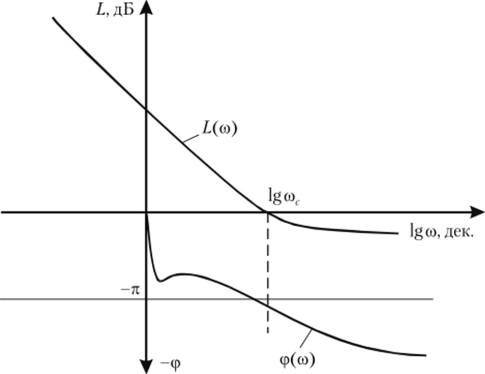
Рис. 4.24. Логарифмические характеристики разомкнутой системы Поскольку логарифмическая амплитудно-частотная характеристика пересекает ось абсцисс позже, чем фазовая частотная характеристика достигает значения <�р_р(со) = -л, то замкнутая система будет неустойчива.