Ортогональный центральный композиционный план (ЦКП)

План, которому соответствует функция отклика.

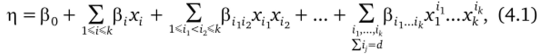
представляющая собой полином степени d от переменных х_1; х₂, …, х_к, называют планом порядка d, если он позволяет получить несмещенные (раздельные) МНК-оценки неизвестных параметров |3₀, {р,}, {(3₍₁,₂},…, {р^ _ik}. Число неизвестных параметров в (4.1) равно C_k+d.

Для аппроксимации области экстремума обычно используется полином второй степени.

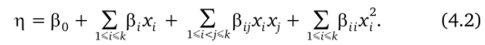
При аппроксимации области экстремума гиперповерхностью второго порядка возникает задача выбора плана эксперимента. Для построения планов второго порядка нельзя непосредственно воспользоваться факторными экспериментами, в которых переменные варьируются на двух уровнях. Эти эксперименты не позволяют получить раздельные оценки параметров (3₀, {р,}, так как для нихх₃ = х₂ = … = х³ = 1, поэтому при построении планов второго порядка применяются факторные эксперименты, в которых переменные варьируются на трех или более уровнях. В ПФЭ типа З^к число различных точек плана N = З^к. Однако использование для построения планов второго порядка таких ПФЭ нецелесообразно, так как из;

е. i г ^ лл ii (fc + 1)№ + 2).

быточность опытов N — (р + 1), где р + 1 = —-;

число неизвестных параметров в (4.2), при этом велика.

В ЦКП переменные варьируются на пяти уровнях.

Рассмотрим пример построения ЦКП, когда число факторов к = 3. ПФЭ 2³ образует ядро композиционного плана (на рис. 4.1 ядро плана изображено кружочками и зачерненными точками). В качестве дополнительных точек для наблюдений возьмем еще шесть так называемых «звездных» точек с координатами (-dj, 0, 0), (а_1; 0, 0), (0, -а₂, 0), (0, а₂, 0), (0, 0, -а₃), (0, 0, а₃) (на рис. 4.1 отмечены крестиками). Кроме указанных точек при построении композиционного плана используют п₀ параллельных (повторных) опытов в его центре (зачерненный квадрат на рис. 4.1). Они необходимы для проверки гипотезы адекватности модели и получения информации о центре плана.

Матрица плана (см. рис. 4.1) при п₀ = 2 имеет вид.

Рис. 4.1. цкп.

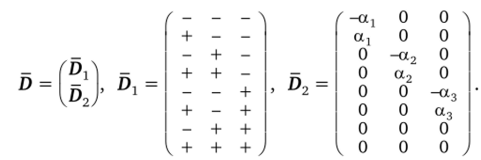
План представляет собой композицию или соединение двух планов и поэтому называется композиционным. Поскольку точки построенного композиционного плана расположены симметрично относительно центра, то его называют центральным. В рассмотренном плане число опытов N = 2³ + + 2×3 + 2 = 16, а в ПФЭ 3³N = 27.

Аналогично строятся центральные композиционные планы второго порядка для произвольного числа факторов к, при этом каждый из факторов х, варьируется на пяти уровнях: -а" -1, 0, а" 1 (i = 1, 2,…, к). ЦКП второго порядка получается достраиванием двухуровневого факторного плана типа 2^к~⁴ (О < q < к) путем присоединения к нему «звездных» и центральных точек. Факторный план типа 2^к~^ч в этом случае называют ядром плана.

Матрица ЦКП второго порядка.

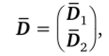
где D, — матрица факторного плана,.

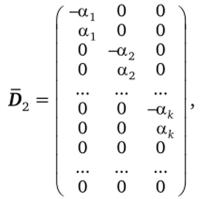
D₂ — матрица «звездного» плана, имеющая порядок (2/с 4- п₀) х к. Число наблюдений.

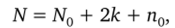
где N₀ — число наблюдений в тючках ядра плана, 2к — число.

«звездных» точек, п₀ — число наблюдений в центре плана.

Число различных точек плана.

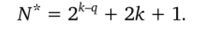
Далее будем рассматривать планы, для которых а, = а (i = 1, 2, …, к). Все точки таких планов расположены на трех гиперсферах, одна из которых вырожденная. Необходимым условием существования несмещенных МНК-оценок (р + 1) неизвестных коэффициентов в уравнении (4.2) при выборе регулярной дробной реплики в качестве ядра плана является условие р < N*. При q = 0 это условие является достаточным для любого к > 2.

В табл. 4.1 приведена матрица независимых переменных ЦКП второго порядка. Знаки «+» и «-» означают, что переменные х_г, х₂, …, х_к и их парные взаимодействия принимают положительные либо отрицательные значения.

Дробная реплика, используемая в качестве ядра ЦКП, Таблица 4.1. Матрица независимых переменных ЦКП второго порядка.

должна удовлетворять определенным требованиям, иначе ЦКП не позволит получить несмещенные МНК-оценки неизвестных коэффициентов в (4.2), т. е. он не будет планом второго порядка.

Дробная реплика типа 2^к ~⁴ может быть ядром ЦКП второго порядка тогда и только тогда, когда два любых парных взаимодействия для этой реплики по модулю не равны между собой, т. е. когда.

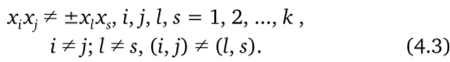
ЦКП будет планом второго порядка в том и только в том случае, когда матрица независимых переменных, соответствующая полиному второй степени, имеет максимальный ранг. Пусть некоторые парные взаимодействия в ядре плана по модулю равны, т. е. нарушается условие (4.3). Тогда столбцы матрицы независимых переменных, соответствующие этим взаимодействиям, будут без учета знака также равны и, следовательно, линейно зависимы. Пусть теперь выполняется условие (4.3). Тогда ни один столбец матрицы независимых переменных не может быть представлен в виде линейной комбинации ее остальных столбцов и, значит, ее ранг будет максимальным.

Можно сделать вывод, что по построению ЦКП второго порядка два любых парных взаимодействия в точках ядра плана по модулю не равны, т. е. выполняется условие (4.3).

Основная особенность ЦКП заключается в том, что они позволяют применять методы последовательного планирования эксперимента. Сначала для анализа поверхности отклика строится ДФЭ типа 2^к~^ч. Далее, если результаты анализа не удовлетворяют исследователя, то ДФЭ достраивается до ЦКП и проводится более полное изучение поверхности отклика. В этом случае композиционные планы дают выигрыш по числу опытов по сравнению с другими планами. Эти планы можно применять и при непосредственном построении функции отклика в виде полинома (4.2).