Разброс. 
Политический анализ и прогнозирование в 2 ч. Часть 2

Следующая задача заключается в измерении разброса наблюдений порядковой шкалы вокруг медианы. Для этого чаще всего используется разбиение ранжированного ряда на четверти — четыре равные по числу элементов части. Значения, разбивающие ряд на четверти, называются квартилями, и всего их три (а не четыре!). Первая квартиль (Q,) «отсекает» нижние 25% наблюдений, выше ее — 75% элементов ряда. Вторая квартиль совпадает с медианой Q₂ = Me, ниже и выше ее находятся по 50% наблюдений. Ниже третьей квартили (Q_}) находится 75% наблюдений, выше — 25%. Первая квартиль называется также нижней, третья — верхней. Нижняя квартиль делит пополам объем от первого наблюдения до медианы, верхняя делит пополам объем от медианы до последнего наблюдения.

Собственно мерой разброса (вариации) на порядковом уровне является межквартильный размах (Н). Он представляет собой разность между третьей и первой квартилями:

Чем больше межквартильный размах, тем сильнее колебания наблюдений вокруг центра — медианы.

Принципиально расчет квартилей похож на расчет медианы — в обоих случаях мы работаем с ранжированными рядами и делим их на некоторые равные части. При этом формулы вычисления квартилей довольно громоздки, и мы не будем их здесь приводить. Ограничимся вычислением квартилей в программе Excel, оттолкнувшись от следующего примера.

Вновь 11 экспертов оценивают влиятельность некоторого политика, причем используется метод Дельфи (см. главу 4). Напомним, что этот метод предполагает оценку свойства одной и той же группы объектов в несколько туров; между турами идет управляемая заочная процедура обмена аргументами. Оценки первого тура и оценки четвертого тура см. в табл. 6.3.

Таблица 6.3

Как изменилось мнение группы от первого тура к четвертому? Чтобы дать этому изменению количественную характеристику, воспользуемся медианой и квартилями.

Упражнение 6.3

1. Рассчитайте значение первой квартили для оценок первого тура. Для этого воспользуйтесь функцией «КВАРТИЛЬ». Ее аргументами являются диапазон значений и номер квартили (см. рис. 6.8).

Рис. 6.8.

• 2. Аналогичным образом рассчитайте вторую (медиана) и третью квартиль для оценок первого тура.
• 3. Рассчитайте межквартильный размах оценок первого тура, используя формулу (6.4).
• 4. Повторите расчеты п. 1−3 для оценок четвертого тура. Результаты и используемые функции показаны на рис. 6.9.

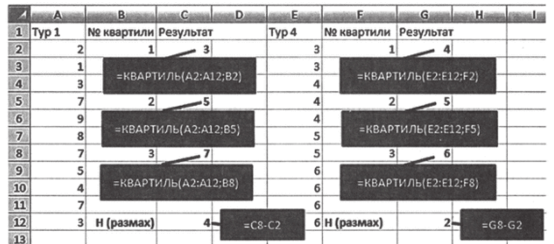
Рис. 6.9

Итак, от первого тура к четвертому средняя оценка группы не изменилась — вторая квартиль, она же медиана, в обоих случаях равна пяти. Однако существенно сократился разброс оценок вокруг медианы: в первом туре межквартильный размах Н составляет 4, в четвертом — 2. Распределение как бы «сжалось» вокруг средней. Это хорошо видно на гистограммах распределения (рис. 6.10); они строятся на основании таблицы частотных распределений точно таким же образом, как для номинальных переменных.

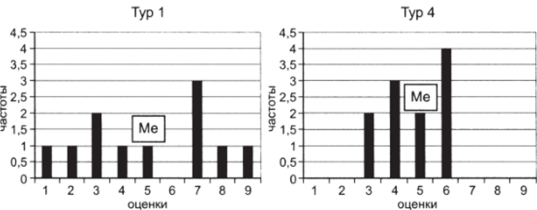
Рис. 6.10.

Таким образом, после обмена аргументами эксперты продемонстрировали гораздо большее единодушие в своих суждениях. В методологии экспертных опросов это является основанием для большего доверия к среднегрупповой оценке.

На порядковом уровне измерения мы можем использовать меры центральной тенденции и разброса номинального уровня (но не наоборот!). Следует запомнить одно очень важное правило: при использовании более точных измерительных шкал применимы все операции для более простых шкал; обратное неверно. Так, для порядковых переменных мы можем рассчитать моду и относительную частоту немодальных значений. Для первого тура в нашем примере мода равна 7, суммарная относительная частота остальных значений — примерно 0,83. Но мы не можем рассчитывать медиану и квартили на номинальном уровне.

Наиболее богатыми возможностями для описательностатистических исследований мы располагаем на параметрических уровнях — интервальном и относительном. Вопервых, здесь могут быть использованы все инструменты номинального и порядкового уровней (целесообразность их применения мы обсудим отдельно). Во-вторых, для величин имеются специфические, работающие только с параметрами описательно-статистические инструменты.

Некоторые из них уже знакомы читателю по предыдущему материалу. Основной оценкой центра распределения является среднее арифметическое. Еще раз приведем эту формулу:

Существуют и другие меры центральной тенденции, такие как среднее геометрическое или среднее гармоническое, но они в политической науке используются сравнительно редко.

Ключевыми показателями вариации являются уже знакомые дисперсия

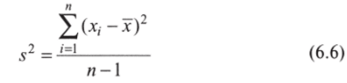
и стандартное отклонение

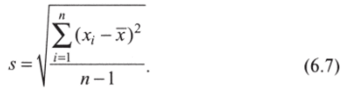
Эти меры разброса мы также рассматривали в разделе, посвященном особенностям статистической методологии.

Наиболее простой мерой разброса является размах. Размах (?) представляет собой разность между максимальным и минимальным значением:

Размах показывает, в каком интервале колеблется переменная, и это достаточно грубая оценка ее вариации. Так, например, переменные А и В в табл. 6.4 обладают одинаковым размахом, но их колеблемость существенно различна.

Таблица 6.4

Еще одной полезной мерой разброса является коэффициент вариации. Покажем его применение на примере.

Пусть имеется две переменных: «поддержка партии С» и «поддержка партии D» (см. табл. 6.5).

Таблица 6.5

Отклонения от средних для каждого случая у обеих партий одинаковы; соответственно, одинаковы и основные показатели вариации: дисперсия (10,64), стандартное отклонение (=3,3) и размах (9). Однако ясно, что относительно своей средней партия С колеблется значительно сильнее, нежели партия D. Именно это различие позволяет уловить коэффициент вариации (v). Он представляет собой отношение стандартного отклонения к средней арифметической, умноженное на 100%:

Для примера выше коэффициенты вариации приближенно равны 197% и 19% для С и D соответственно. Таким образом, коэффициент вариации является относительным показателем разброса данных, учитывающим не только значения отклонений, но и значение средней величины.

Упражнение 6.4

В табл. 6.6 приведены результаты президентских выборов в США 2008 г. для двух основных кандидатов — Барака Обамы и Джона Маккейна. Таблица в электронном виде доступна по ссылке http://polit.msu.ru/kaf/lab_quant/, а также на сайте «Электоральная география»^[1].

1. Рассчитайте среднюю арифметическую, используя функцию «=СРЗНАЧ».

Таблица 6.6

• 2. Рассчитайте размах. Для этого ранжируйте значения переменной, используя опцию «Сортировка». Затем вычтите минимальное значение из максимального значения.
• 3. Рассчитайте дисперсию (функция «=ДИСП») и стандартное отклонение («=СТАНДОТКЛОН»).
• 4. Рассчитайте коэффициент вариации по формуле (6.9). Все функции для расчета описательно-статистических

показателей поддержки Б. Обамы показаны на рис. 6.11; географию поддержки Д. Маккейна проанализируйте самостоятельно.

Рис. 6.11.

• [1] http://www.electoralgeography.com/new/ru/countries/u/usa/ssha-prezidentskie-vybory-2008.html (Не забудьте убрать из таблицы данные постране в целом!)