Создание скрытого канала

С помощью алгоритма цифровой подписи, например алгоритма Эль-Гамаля, может быть организован скрытый (подсознательный) канал передачи информации. При этом скрываемое сообщение содержится в цифровой подписи передаваемых открытых сообщений. Извлечь скрытую таким образом информацию может только человек, обладающий общим с отправителем секретным ключом.

Проверяющая сторона (цензор) С не только не сможет прочитать сообщение, передаваемое по скрытому каналу, но у него вообще нет ни малейшего представления о существовании такого сообщения. Проверяющий С видит, как подписанные безобидные сообщения передаются между отправителем и получателем, но реальная передаваемая информация проходит незаметно для него, но скрытому каналу.

В общем случае организация скрытого канала выглядит следующим образом:

• 1) отправитель, А создает безобидное сообщение;
• 2) используя общий с получателем секретный ключ &_АВ, А подписывает безобидное сообщение, пряча свое подсознательное сообщение в подписи;
• 3) А посылает подписанное сообщение по открытому каналу передачи данных;
• 4) проверяющий С читает сообщение и проверяет подпись. Не обнаружив ничего подозрительного, он передает сообщение дальше;
• 5) получатель В проверяет подпись иод безобидным сообщением, убеждаясь в том, что сообщение получено от А,
• 6) В игнорирует безобидное сообщение и, используя общий с отправителем секретный ключ k_AB, извлекает подсознательное сообщение.

В действительности, алгоритм создания скрытого канала в подписях практически не отличим от нормального алгоритма создания подписи. Для системы цифровых подписей Эль-Гамаля единственным отличием является то, что в роли случайного числа k выступает подсознательное сообщение MS.

Сначала формируются общие (открытые) параметры системы Эль-Гамаля, т. е. числа р и g, выбор которых осуществляется так же, как и в системе Диффи — Хеллмана (р — большое простое число,р = 2q + 1,1 <

— 1, g^q mod p* l, q — большое простое число). Затем отправитель выбирает случайное число Ху 1<�х<�р-1и вычисляет у = g^x mod р. В системе Эль-Гамаля число х является личным ключом отправителя, число у — его открытым ключом. Для организации скрытого канала число х должно быть общим секретным ключом абонентов, т. е. отправитель должен заранее надежным способом передать число х получателю.

Отправитель, А создает безобидное сообщение М и скрытое сообщение MS, такие, что: 0 < М < р и 0 < MS < р — 1, MS — взаимно простое с р — 1. Отправитель, А формирует цифровую подпись сообщения, вычисляя:

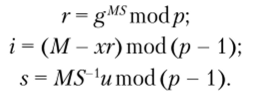
А формирует подпись и в то же время создает скрытый канал, пересылая сообщение М и подпись (г, s) получателю В.

Проверяющая сторона С может удостовериться в подлинности цифровой подписи сообщения М, проведя стандартные для этого случая вычисления:

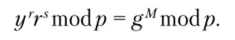
Получатель В также проверяет подлинность подписи, удостоверяясь в том, что сообщение получено именно от того отправителя, с которым организован скрытый канал. Затем получатель В, зная общий секретный ключ х, извлекает скрытое сообщение:

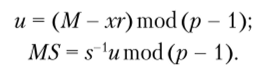
Как видно, для получения MS требуется вычислить число, обратное s по модулю р — 1. Таким образом, s должно быть взаимно простым с р — 1. Этого можно добиться, варьируя значение сообщения М.

В приведенных формулах вместо М может использоваться его хэш-значение h (M).

Пример 3.32.

Пусть выбраны параметры системы Эль-Гамаля р = 2 • 5 + 1 = 11 (q = 5), g = = 2,2⁵ mod 11 = 10¹. Пусть абонент выбрал личный ключ х = 8 и вычислил открытый ключ у = 2^s mod 11=3. Пусть абонент надежным способом передал получателю секретный ключ х = 8.

Пусть теперь абонент хочет передать скрытое сообщение MS = 9, используя цифровую подпись Эль-Гамаля и открытое сообщение М = 5. MS = 9 взаимно просто с р — 1 = 10. Абонент вычисляет: г = g^MS mod р — 2⁹ mod 11 = б, и — = (М — xr) mod (р — 1) = (5 — 8 • 6) mod 10 = 7. Используя расширенный алгоритм Евклида, он получает MS ¹ mod (р — 1) = 9 ' mod 10 = 9. Затем вычисляет s = MS 'и mod (р - 1) = 9? 7 mod 10 = 3.

Полученное число s = 3 взаимно просто ср — 1 = 10, значит, получатель сможет восстановить скрытое сообщение MS. Абонент отсылает сообщение М = 5 и подпись (6, 3) получателю. Любой проверяющий может убедиться в подлинности подписи, сравнив значения y^rr^s mod р = З⁶ • 6³ mod 11 = 10 и g^M mod р = = 2⁵ mod 11 = 10, 10= 10.

Получатель также проверяет цифровую подпись под сообщением М и удостоверяется в том, что получил сообщение от нужного абонента. Затем он вычисляет: и = (М — xr) mod (р — 1) = (5 — 8 • 6) mod 10 = 7. Используя расширенный алгоритм Евклида, он получает значение s ¹ mod (р — 1) = 3 ¹ mod 10 = 7. Тогда MS = = s 'и mod (р — 1) = 7 • 7 mod 10 = 9. Скрытое сообщение восстановлено правильно.

Пример 3.33.

Пусть выбраны параметры системы Эль-Гамаля р = 11 и g = 2. Абонент получил сообщение М = 8 с подписью (7, 1), из которого требуется извлечь скрытое сообщение. Абонент также знает секретный ключ скрытого канала х = 3 и открытый ключ отправителя у = 8.

Сначала абонент удостоверяется в подлинности подписи и отправителя сообщения, сравнивая y^rr* mod р = 8⁷ • 7^[1] mod 11 = 3 и g^M mod р = 2⁸ mod 11 = 3,3 = 3, подпись верна. Затем абонент извлекает скрытое сообщение. Для этого он вычисляет и = (М — xr) mod (р — 1) = (8 — 3 • 7) mod 10 = 7, с помощью расширенного алгоритма Евклида получает значение s~^[1] mod (р - 1) = 1 ¹ mod 10 = 1, MS = s~^[1]u mod (p — 1) = 1 • 7 mod 10 = 7.

Скрытый канал может быть организован и с использованием других рандомизированных схем цифровой подписи, например на основе схем Онга — Шнорра — Шамира, Рабина^[1]. Создаваемые скрытые каналы имеют довольно высокую пропускную способность: так, при использовании схемы Эль-Гамаля она составит около половины длины подписи — длина MS сопоставима с длиной р.

Главным же недостатком такого подхода является необходимость передачи получателю личного ключа х другого абонента (в схеме Рабина передачи ключа не требуется). Передачи секретного ключа в схеме Эль-Гамаля можно избежать, используя варианты цифровой подписи с составным модулем^[5].

Для защиты от организации скрытого канала на основе схемы Эль-Гамаля в протокол цифровой подписи вводится арбитр D, который участвует в выборе случайного элемента (числа к) и имеет возможность проверить, что при формировании подписи было использовано именно это число, не зная его значения^[6]. В обычный протокол формирования цифровой подписи добавляются следующие шаги:

• 1) отправитель, А сообщения выбирает случайное число к, формирует значение г = g^kmodp и отправляет его арбитру D, выступающему в роли проверяющей стороны;
• 2) арбитр D выбирает случайное число к' и направляет его отправителю;
• 3) отправитель использует кк' в качестве случайного числа для формирования подписи — так, он вычисляет первую часть подписи как г' = g** mod/?. Подпись направляется арбитру D;
• 4) теперь D может удостовериться в том, что отправитель использовал именно число kk проверяя выполнение равенства г' = г* mod/?.

Существуют рандомизированные схемы цифровой подписи (схемы на основе решения системы сравнений), не допускающие встраивания скрытого канала^[7].

• [1] Возможные способы защиты информации от передачи данных по скрытому каналу в системах электронной цифровой подписи / И. В. Куржеевский [и др.] // Естественные и математические науки: вопросы и тенденции развития: материалы международной заочной научно-практической конференции. Новосибирск: СибАК, 2013. С. 57—67; Молдовян II. А. Практикумпо криптосистемам с открытым ключом.
• [2] Возможные способы защиты информации от передачи данных по скрытому каналу в системах электронной цифровой подписи / И. В. Куржеевский [и др.] // Естественные и математические науки: вопросы и тенденции развития: материалы международной заочной научно-практической конференции. Новосибирск: СибАК, 2013. С. 57—67; Молдовян II. А. Практикумпо криптосистемам с открытым ключом.
• [3] Возможные способы защиты информации от передачи данных по скрытому каналу в системах электронной цифровой подписи / И. В. Куржеевский [и др.] // Естественные и математические науки: вопросы и тенденции развития: материалы международной заочной научно-практической конференции. Новосибирск: СибАК, 2013. С. 57—67; Молдовян II. А. Практикумпо криптосистемам с открытым ключом.
• [4] Возможные способы защиты информации от передачи данных по скрытому каналу в системах электронной цифровой подписи / И. В. Куржеевский [и др.] // Естественные и математические науки: вопросы и тенденции развития: материалы международной заочной научно-практической конференции. Новосибирск: СибАК, 2013. С. 57—67; Молдовян II. А. Практикумпо криптосистемам с открытым ключом.
• [5] Возможные способы защиты информации от передачи данных по скрытому каналу в системах электронной цифровой подписи / И. В. Куржеевский [и др.]. С. 57—67.
• [6] Молдовян Н. А. Практикум по криптосистемам с открытым ключом.
• [7] 1 Там же.