Существенно особая точка

Остаётся исследовать повеление функции f (г) в окрестности существенно особой точки. Мы видели, что в случае устранимой особой точки а функция f (z) стремится к определённому конечному пределу с₀, когда точка z стремится к точке а (п. 2); в случае полюса функция стремится также к определённому пределу, равному бесконечности (п. 3). Если же а есть существенно особая точка, то здесь имеет место следующая теорема, принадлежащая Вейерштрассу: каково бы ни было постоянное число Л, конечное или бесконечное, существует последовательность точек z_lt z₂,…, z_n.сходящаяся к существенно особой точке а, такая, что имеем: lim f (z_n) = A.

Z_n-Hl

Короче это можно формулирован" так: в сколь угодно малой окрестности существенно особой точки функция f (z) принимает значения, сколь угодно близкие к любому наперёд заданному числу, конечному или бесконечному.

Замечали е. Чтобы дать геометрическую характеристику теоремы Вейерштрасса, будем изображать точками плоскости w значения функции w = f (z), принимаемые ею в сколь угодно малой окрестности 0<|z —я|<�о существенно особой точки а. Теорема Всйершграсса утверждает, что любая точка А плоскости w является предельной точкой для множества значений, принимаемых функцией w =/ (г) в сколь угодно малой окрестности точки а.

Переходя к доказательству теоремы Вейерштрасса, предположим сначала, что Л = оо. Покажем, что существует последовательность точек z_n, lim z_n=a> таких, что имеем: Нт/(г_я) = оо. Обозначая для.

г_п -* а

сокращения через P (z — а) правильную часть разложения Лорана (11), содержащую положительные степени z — а и свободный член, а через.

Q ^ его главную часть, содержащую отрицательные степени. z—.д, можем переписать (11) в виде:

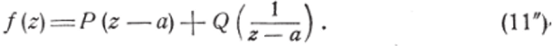
Что касается правильной части Р (z — д), то при любом стремлении точки z к точке а имеем:

Полагая в главной части Q

будем иметь:

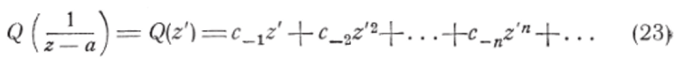
Так как рях Q сходится всюду, кроме точки z = д (§ 1, п. 2)^.

то ряд (23), очевидно, будет сходящимся во всей плоскости комплексного переменного z. Функция Q (z') по теореме Лиувилля (гл. V, § 2, п. 9) не может быть ограниченной во всей плоскости комплексного переменного z т. е. какое бы натуральное число N мы ни взяли, найдётся точка z'_N, такая, что будем иметь |Q (^)|^>M.

Заставляя N пробегать значения 1,2, 3,…, я,. ., мы получим последовательность точек z'_v z'_v z’y…, z'_n,…_t стремящуюся к бесконечности и такую, что будем иметь: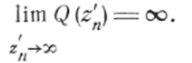

Возвращаясь к прежнему переменному z, мы видим на основании (22), что последовательность точек z'_n преобразуется в последовательность точек z_v z_nf…, сходящуюся к точке а, такую, что имеем:

Заставляя точку z стремиться к точке а, проходя последовательность точек z_n, усматриваем из равенства (11″) на основании равенств (21) и (24):

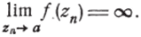
Пусть теперь А есть произвольное конечное комплексное число. Может случиться, что в произвольно малой окрестности точки а существует точка z такая, что имеем f (z) = A. В этом случае теорема ВеЙерштрасса справедлива. Таким образом, мы можем предположить, что в достаточно малой окрестности точки а функция f (z) не равна Л.

Если так, то функция.

j ²) — л окрестности точки а, кроме точки z = a_y которую она имеет в качестве существенно особой точки [потому что z=.a существенно особая точка для f (z). По доказанному существует последовательность точек 2_П, сходящаяся к точке а, такая, что имеем: Нш ср (*_п) = оо,.

г_л-*а

откуда следует: lim/(a:_n) = Л, что и нужно.

г_п-* а