Плоское деформированное состояние полимерного цилиндра в условиях термовязкоупругости

Из представленных графиков видно, что гипотеза об отсутствии объемной деформации ползучести приводит к завышенным значениям напряжений в конце процесса ползучести. При t = 13.4 ч максимальные величины напряжений отличаются на 35%, а — на 27%. Ключевые слова: нелинейная ползучесть, полимерный цилиндр, высокоэластические деформации, уравнение Максвелла-Гуревича, метод конечных элементов… Читать ещё >
Плоское деформированное состояние полимерного цилиндра в условиях термовязкоупругости (реферат, курсовая, диплом, контрольная)
Аннотация
Получены разрешающие уравнения для определения напряженно-деформированного состояния толстостенной полимерной цилиндрической оболочки, находящейся в условиях плоского деформированного состояния с учетом изменения температуры и высокоэластических деформаций. В качестве закона, описывающего связь между напряжениями и деформациями ползучести, используется нелинейное уравнение Максвелла-Гуревича. Решение производится численно при помощи метода конечных элементов.
Ключевые слова: нелинейная ползучесть, полимерный цилиндр, высокоэластические деформации, уравнение Максвелла-Гуревича, метод конечных элементов, вязкоупругость, модуль высокоэластичности, плоское деформированное состояние, температура.
Рассмотрим вязкоупругий толстостенный цилиндр, подверженный действию внутреннего и внешнего давления, достаточно протяженный по своей длине.
Данный цилиндр будет находиться в условиях плоского деформированного состояния (ПДС). Пусть температура цилиндра является функцией от радиуса и времени. Для полимеров все упругие и релаксационные характеристики сильно зависят от температуры, поэтому они также будут функциями координаты и времени.
В такой постановке данная задача решается методом конечных разностей для полимерных цилиндров в работах [1, 2], и для бетонных — в работах [3−5]. В настоящей статье будут получены разрешающие уравнения метода конечных элементов.
Связь между напряжениями и деформациями для плоского деформированного состояния имеет вид:
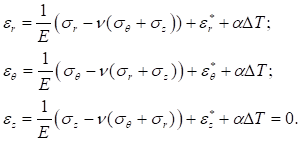
(1).
где, , — деформации ползучести.
Исключим из (1) напряжение :
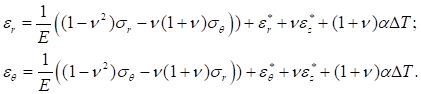
(2).
В теории ползучести используется гипотеза о равенстве нулю объемной деформации ползучести, т. е.
С учетом этой гипотезы соотношения (2) перепишутся в виде:
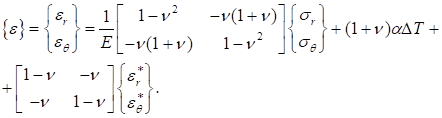
(3).
Выразим из (2) и (3) напряжения через деформации:

(4).
где.
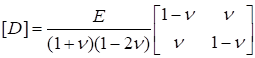
матрица упругих постоянных; — вектор вынужденных деформаций. В случае равенства нулю объемной деформации ползучести вектор запишется в виде:

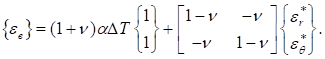
В общем случае вектор имеет вид:

Будет использоваться одномерный элемент с двумя узлами и одной степенью свободы в узле — перемещением (рис. 1).
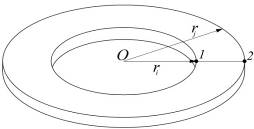
Рис. 1 Одномерный осесимметричный конечный элемент
Связь между перемещениями и деформациями имеет вид:
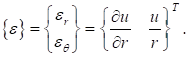
(5).
Функция изменения перемещения в пределах элемента принимается линейной:
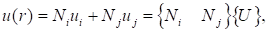
(6).
где.
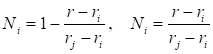
функции формы;
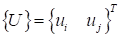
— вектор перемещений в узлах.
Подставим (6) в (5), получим:
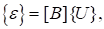

где. (7).
Потенциальная энергия деформации элемента записывается в виде:
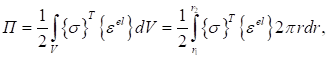
(8).
где.
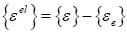
— упругая деформация.
Будем считать, что вынужденные деформации в пределах элемента постоянны. Подставив (4) и (7) в (8), получим:
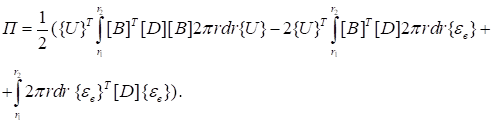
(9).
Окончательно задача сводится к системе линейных алгебраических уравнений:

(10).
где.
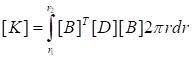
— матрица жесткости;
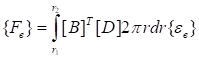
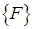
— вклад вынужденных деформаций в вектор нагрузки; — вектор внешних узловых нагрузок.
Для полимеров справедливо нелинейное уравнение Максвелла [6−8], которое для одноосного напряженного состояния имеет вид:
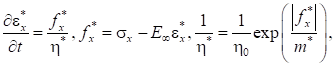
где — модуль высокоэластичности; - начальная релаксационная вязкость; — модуль скорости.
Обобщение этого уравнения для трехосного напряженного состояния было выполнено Г. И. Гуревичем [6]:
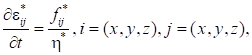
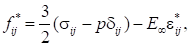
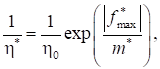
(12).
где.
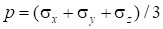
— среднее напряжение; — символ Кронекера.
При этом были приняты следующие допущения:
- 1. Равенство нулю объемной деформации ползучести.
- 2. Коэффициент Пуассона для неупругих деформаций .
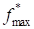
3. Релаксационная вязкость для скоростей роста деформаций, и одинакова и определяется по максимальной функции напряжений .
Полученные уравнения МКЭ позволяют произвести расчет и без этих упрощений. На основе принципа суперпозиции представим трехосное напряженное состояние в точке как сумму трех одноосных состояний:
1.
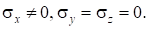
2.
При отсутствии температурных деформаций:
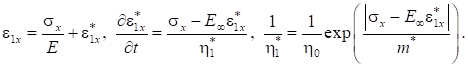
Деформации по осям y и z можно найти через коэффициент Пуассона:
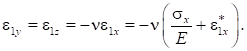
- 3.
- 4.
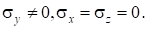
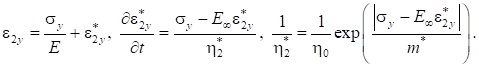

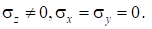
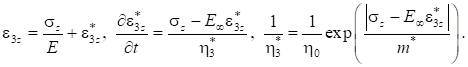
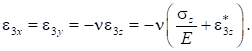
Полная деформация по оси запишется в виде:
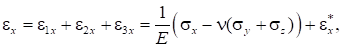
где.
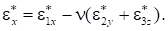
Выражения для остальных деформаций можно получить циклической заменой индексов. Полные деформации ползучести по осям y и z примут вид:

Был выполнен расчет полимерного цилиндра из ЭДТ-10 с внутренним радиусом a = 0.8 см, внешним радиусом b = 2.8 см.
Зависимости модуля упругости и релаксационных констант от температуры для ЭДТ-10 имеют вид [9, 10]:
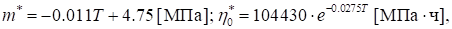
где T — температура в градусах Цельсия.
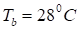
Температура цилиндра при r = b постоянна —, а на внутренней поверхности (при r = a) растет с постоянной скоростью в течение 1.2 часа от до .
На рис. 2 и 3 показаны соответственно графики изменения напряжений и в толще цилиндра при t = 0.4 ч (черная линия), t = 1.2 ч (красная линия) и t = 13.4 ч (фиолетовая линия). Синей линией показано упругое решение при t? 1.2 ч. Штриховым линиям соответствует уточненное решение без учета равенства нулю объемной деформации ползучести.
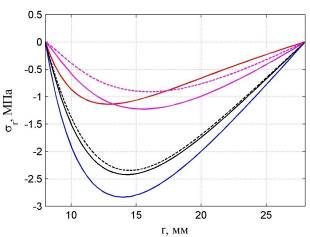
Рис. 2 Распределение напряжений в толще цилиндра
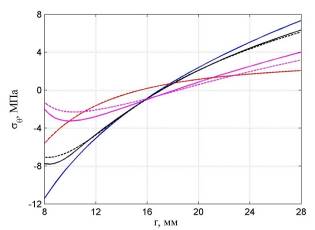
Рис. 3 Распределение напряжений в толще цилиндра
Из представленных графиков видно, что гипотеза об отсутствии объемной деформации ползучести приводит к завышенным значениям напряжений в конце процесса ползучести. При t = 13.4 ч максимальные величины напряжений отличаются на 35%, а — на 27%.
деформация полимерный цилиндрический гуревич.
- 1. Андреев В. И. Некоторые задачи и методы механики неоднородных тел: монография. М.: Издательство АСВ, 2002. 288 с.
- 2. Языев Б. М. Нелинейная ползучесть непрерывно неоднородных цилиндров. Дисс. канд. техн. наук. М., 1990. 171 с.
- 3. Языев Б. М., Чепурненко А. С., Литвинов С. В., Козельская М. Ю. Напряженно-деформированное состояние предварительно напряженного железобетонного цилиндра с учетом ползучести бетона // Научное обозрение. № 11. Часть 3. 2014. С.759−763.
- 4. Литвинов С. В., Козельский Ю. Ф., Языев Б. М. Расчёт цилиндрических тел при воздействии теплового и радиационного нагружений // Инженерный вестник Дона, 2012, № 3 URL: ivdon.ru/ru/magazine/archive/n3y2012/954.
- 5. Языев Б. М., Литвинов С. В., Козельский Ю. Ф. Плоская деформация элементов цилиндрических конструкций под действием физических полей// Инженерный вестник Дона, 2013, № 2 URL: ivdon.ru/uploads/article/pdf/IVD24_yaziev.pdf_1616.pdf.
- 6. Гуревич Г. И. Об обобщении уравнения Максвелла на случай 3 измерений с учетом малых деформаций упругого последействия // Труды ИФЗ АН СССР. 1959. № 2. С. 169.
- 7. Vladimir I. Andreev, Batyr M. Yazyev, Anton S. Chepurnenko. On the Bending of a Thin Plate at Nonlinear Creep//Advanced Materials Research Vol. 900 (2014) pp. 707−710. Trans Tech Publications, Switzerland.
- 8. Vladimir I. Andreev, Anton S. Chepurnenko, Batyr M. Yazyev. Energy Method in the Calculation Stability of Compressed Polymer Rods Considering Creep//Advanced Materials Research Vols. 1004−1005 (2014) pp. 257−260. Trans Tech Publications, Switzerland.
- 9. Бабич В. Ф., Рабинович А. Л. Влияние температуры на механические характеристики некоторых эпоксидных связующих // Физико-химия и механика ориентированных стеклопластиков. 1967. С. 150−153.
- 10. Козельская М. Ю., Чепурненко А. С., Литвинов С. В. Применение метода Галёркина при расчете на устойчивость сжатых стержней с учетом ползучести // Инженерный вестник Дона, 2013, № 2 URL: ivdon.ru/magazine/archive/n2y2013/1714.
References.
- 1. Andreev V.I. Nekotorye zadachi i metody mehaniki neodnorodnyh tel: monografija. M.: Izdatel’stvo ASV, 2002. 288 s. [Disa probleme dhe metoda nл mekanizmin e heterogjene solids: monografi. M.: shtлpia Botuese e DIA, 2002. 288 p.]
- 2. Jazyev B.M. Nelinejnaja polzuchest' nepreryvno neodnorodnyh cilindrov. Diss. kand. tehn. nauk. M., 1990. 171 p. [Nonlinear creep continuously inhomogeneous cylinders. Diss. Cand. tech. Sciences. M., 1990. 171 p.]
- 3. Jazyev B. M., Chepurnenko A. S., Litvinov S. V., Kozel’skaja M. Ju. Nauchnoe obozrenie. № 11. Chast' 3. 2014. S.759−763.
- 4. Litvinov S. V., Kozel’skij Ju. F., Jazyev B. M. Inћenernyj vestnik Dona (Rus), 2012, № 3 URL: ivdon.ru/ru/magazine/archive/n3y2012/954.
- 5. Jazyev B. M., Litvinov S. V., Kozel’skij Ju. F. Inћenernyj vestnik Dona (Rus), 2013, № 2 URL: ivdon.ru/uploads/article/pdf/IVD24_yaziev.pdf_1616.pdf.
- 6. Gurevich G.I. Ob obobshhenii uravnenija Maksvella na sluchaj 3 izmerenij s uchetom malyh deformacij uprugogo posledejstvija. Trudy IFZ AN SSSR. 1959. № 2. p. 169.
- 7. Vladimir I. Andreev, Batyr M. Yazyev, Anton S. Chepurnenko. On the Bending of a Thin Plate at Nonlinear Creep. Advanced Materials Research Vol. 900 (2014) pp. 707−710. Trans Tech Publications, Switzerland.
- 8. Vladimir I. Andreev, Anton S. Chepurnenko, Batyr M. Yazyev. Energy Method in the Calculation Stability of Compressed Polymer Rods Considering Creep. Advanced Materials Research Vols. 1004−1005 (2014) pp. 257−260. Trans Tech Publications, Switzerland.
- 9. Babich V. F., Rabinovich A. L. Fiziko-himija i mehanika orientirovannyh stekloplastikov. 1967. pp. 150−153.
- 10. Kozel’skaja M.Ju., Chepurnenko A.S., Litvinov S.V. Inћenernyj vestnik Dona (Rus), 2013, № 2 URL: ivdon.ru/magazine/archive/n2y2013/1714.