Принцип симметрии для гармонической функции

Как известно, функция V (x, у) называется гармонической в области, если она однозначна в этой области, обладает непрерывными производными до второго порядка включительно и удовлетворяет уравнению Лапласа:

Мы знаем также (гл. II, § 4, п. 5), что если известна функция V, гармоническая в одцоевязной области, то возможно определить, с точностью до придаточного постоянного, функцию U-f-iV комплексного переменного z — л'-f-iy_t аналитическую в этой области; функция U будет также гармонической.

Условимся называть аналитическим продолжением гармонической функции, определенной в области G, гармоническую функцию, определённую в области G., содержащей G, если эта функция совпадает с данной функцией на области G ^]).

Рассмотрим теперь функцию V (х, у), гармоническую в окрестности правильной аналитической дуги у (открытой) и равную нулю на этой дуге. Возможно построить в этой области функцию голоморфную относительно.

z = x-j-/y. Когда точка z описывает дугу т, эта функция U4-iV всё время имеет действительные значения, т. е. точка UIV остаётся на действительной оси. Вследствие п. 4 мы заключаем, что в точках, симметричных относительно дуги, значения функции U—iV будут симметричными относительно действительной оси, а значит, значения функции V противоположны по знаку.

Теперь естественно формулировать такой принцип аналитического продолжения гармонической функции:

Если V есть функция, гармоническая в области G, граница которой содержит правильную аналитическую дугу у [открытую), кроме того, непрерывна на множестве G-j-Т и равна нулю на у, то она может быть продолжена аналитически через у, если придавать ей значения, противо' оложные по знаку в точках. симметричныхг, относительно у.

^J) Очевидно, если возможно аналитически продолжить гармоническую функцию, то это можно сделать только единственным образом. В самом деле, пусть две функции V и V_u гармонические в некоторой области, совпадают на частичной области. Разность и = V — V будет гармонической в данной области и равной нулю в некоторой её части. Образовав функцию комплексного переменного z = x-±-iy вида иiv, аналитическую в ок|>есгносги каждой точки данной области, мы заключаем, что она равна действительной постоянной в части данной области; отсюда следует, что и^О и V = V,.

Резулыаты, установленные в предыдущих пунктах, недостаточны, чтобы доказать эю предложение, и необходимо специальное доказательство. Возможно привести доказательство формулированного принципа к частному случаю, когда дугой у является интервал действительной оси. Для этого поступим следующим образом. Пусть z = z{t), a есть уравнение дуги у. Считая t за комплексное переменное, мы видим, что существует функция z (t), голоморфная в окрестности интервала (а, Ь) действительной оси и дающая взаимно однозначное соответствие между этой окрестностью и окрестностью дуги 7; когда t описывает интервал (а, Ь), точка z описывает дугу у. Образовав функцию U -4-/V, голоморфную относительно z в части окрестности дуги у, принадлежащей С?, мы видим, что она будет как функция t голоморфна с некоторой стороны интервала {а, Ь) действительной оси. Следовательно, V есть функция, гармоническая от координат точки t с одной стороны интервала {а, Ь) действительной оси и принимающая значение нуль на этом интервале. Если мы предположим теорему верной в этом частном случае, то V аналитически продолжается через (д, Ь), когда мы ей придаём значения, противоположные по знаку в точках, симметричных относительно интервала (д, Ь). Таким образом, V становится гармонической функцией во всей окрестности интервала (а, Ь) и, значит, голоморфной относительно t в этой окрестности. Возвращаясь к переменному z, мы заключаем, что U -f- iV будет голоморфной относительно z в окрестности дуги у и, следовательно, V— гармонической от координат точки z в этой окрестности.

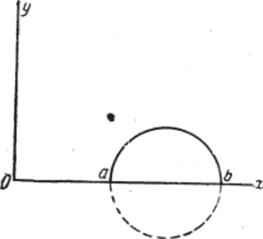
Фиг. 109.

Итак, нам достаточно установить следующее предложение: если V есть функция, гармоническая внутри полукруга с диаметром ab на действительной оси, непрерывная на этом полукруге, включая его границу, и равная нулю на диаметре аЪ, то она совпадает с функцией, гармонической внутри всего круга (фиг. 109).

Определим функцию и (х, у) в круге С, включая его границу, посредством условий:

• 1) и (х, у) — V (х. у) в первом полукруге (например верхнем),
• 2) //(.г, = — V (x, у) во втором полукруге

и покажем, что и (х, у) есть функция, гармоническая внутри круга С радиуса /?.

В самом деле во-первых, очевидно, что и (х, у) есть функция, непрерывная внутри круга С, потому что её значетя на диаметре, равные нулю, совпадают с предельными как из верхней, так и из нижней половины круга, в остальных же точках круга С она совпадает либо с V (лг, у), либо с —V (х, у). Во-вторых, легко обнаружить, что значение её в каждой точке, внутренней к кругу С, равно среднему арифметическому её значений на окружности любого достаточно малого радиуса с центром в этой точке. Действительно, это будет для точек, лежащих над диаметром, потому что в этой области и (дг, у) = V (х, у) и V есть функция гармоническая (гл. IV, § 3, п. 8); то же самое очевидно для точек, лежащих под диаметром, так как здесь u (x_t у) = =z—V (x, y), и, значит, и есть функция гармоническая; наконец, в точке (г₀, уо), лежащей на диаметре, и равно нулю, и легко показать, что.

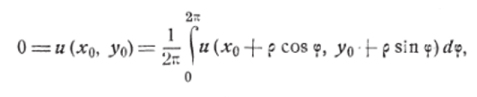
так как подинтегральная функция в пределах (к, 2п) имеет значения, противоположные, но знаку с её значениями в пределах (0, п).

Итак, функция и{х, у) будет непрерывной внутри круга Сив каждой его точке удовлетворяет условию:

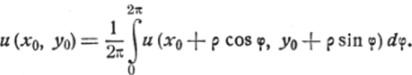
Этого же достаточно для заключения о том, что и {лг, у) есть гармоническая функция внутри С ^J).

Возможно, наконец, обобщить доказанное свойство об аналитическом продолжении через правильную аналитическую дугу гармонической функции V, заменяя условие обращения в нуль на дуге тем условием, что функция, определённая''с одной стороны от дуги, принимает на дуге, сохраняя непрерывность, значения, образующие аналитическую функцию параметра /, входящего в уравнение дуги.

Действительно, определим достаточно малые окрестности‘дуги у и интервала (а, Ь)_у которые взаимно однозначно отображаются при помощи функции z—z (t). Пусть (c)(f) — данная аналитическая последовательность значений; -очевидно, её мы можем рассматривать как голоморфную функцию от t в указанной окрестности интервала (я, b), беря эту окрестность достаточно узкой. Полагая g (z) за у [t (^[1])], мы получаем функцию g (z), голоморфную в окрестности дуги у и принимающую на этой дуге у действительные значения? (f), данные по условию.

Если g (z)= Р (х, y)-{-iQ{x, у), то Р, Q будут гармоническими в окрестности дуги у, причём на дуге у функция Р пршжмает значения 9(f). Следовательно, разность V (x, у) — Р (х, у) есть функция, гармоническая с одной стороны от дуги у, обращающаяся, сохраняя непрерывность, в нуль на этой дуге; по доказанному она может быть продолжена через дугу у и, следовательно, то же заключение можно сделать относительно V (x,~y).

Доказанный в п. 5 принцип Шварца аналитического продолжения функции комплексного переменного является частным случаем только что установленного предложения о продолжении гармонической функции. Болес того, мы можем теперь сказать, что для аналитического продолжения функции комплексного переменного достаточно, чтобы её действительная или мнимая часть принимала на дуге аналитическую последовательность значений. В этом случае действительная или мнимая часть функции будет функцией гармонической, продолжаемой через дугу, и отсюда заключаем, что и сама функция комплексного переменного обладает тем же свойством.

• [1] И. И. Привалов, Sur les fonctions harmoniques, Математическийсборник, т. XXXII.