Свойства и пределы гиперболического роста

Гиперболический рост обладает одним важным свойством: такое развитие динамически самоподобно. Гиперболический рост наблюдается в большом числе экспериментальных зависимостей, когда в системе имеется большое число степеней свободы и многофакторный процесс обладает статистической стационарностью. В этих условиях наблюдается наличие масштабной инвариантности, скейлинга процесса, что приводит к предположению о его автомодельности. Смысл этой основной гипотезы сводится к утверждению о постоянстве относительной скорости роста системы:

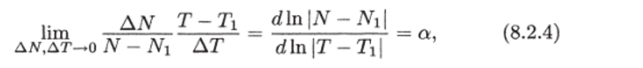
где N, Т — опорные значения численности и времени. В большинстве случаев N = 0 и N положительно. Из соотношения (8.2.4) следует, что самоподобный рост должен описываться степенными законами вида:

Здесь С и а — постоянные, а время отсчитывается от некоторого момента Т. В автомодельных процессах проявляется постоянство отношений изменений численности населения и времени.

Самоподобие реализуется в определенных пределах. Границы автомодельности определяются микропараметрами системы. Для роста человечества границы автомодельности определяются дискретностью численности и характерным временем — временем одного поколения.

Простейший пример автомодельного роста при а = 1 — это линейный рост, при q = — 1 — гиперболический рост. Оказывается, что в эпоху начального роста человечества динамика роста хорошо аппроксимируется линейной функцией. Далее, на более поздних временах в течение длительного времени рост человечества хорошо описывается гиперболической функцией.

Если изобразить гиперболический рост в двойном логарифмипеском масштабе, получится прямая линия. Это означает, что если население увеличилось в 10 раз, то и время, отсчитываемое от определенного момента, тоже изменилось в 10 раз. Из рис. 8.9 видно, что линейный рост обладает тем же свойством самоподобия, а экспоненциальный рост этим свойством не обладает. Рост по гиперболе обращается в бесконечность по мере приближения к точке расходимости — режиму с обострением. В терминологии демографов это явление называется демографическим взрывом. В реальных условиях в этой области вступают факторы, ограничивающие рост.

Формула (8.1.4) имеет свойства, которые не могут удовлетворить исследователей. Из нее следует, что расходимость (демографический взрыв) наступит в самое ближайшее время: Т = 2025 год. В то же время демографические данные свидетельствуют, что относительная скорость роста человечества начиная с I960 г. постепенно падает. Ясно, что если теория претендует на описание современного состояния динамики численности человечества, она должна быть модифицирована. Кроме того, гиперболический рост приводит к абсурдному результату и в далеком прошлом. Согласно ей 20 млрд лет назад (время возникновения Вселенной) на Земле должно было существовать уже 10 человек. Следовательно, требуется модификация теории и на малых временах.

Таким образом, автомодельное решение ограничено как в будущем, так и в прошлом. Это соответствует результату Баренблата (1985), который показал, что автомодельные решения, подобные гиперболическому росту, верны только как промежуточно асимптотические.