Непрерывные случайные векторы

Пусть (^[, …, ^") — «-мерный случайный вектор с функцией распределения F (x…х_п). Если существует неотрицательная функция f (xj,…, х») такая, что для любых …, х"

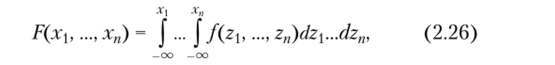
то (?₁₍…, %") называется непрерывным случайным вектором. Функция f (x 1, …, х") называется плотностью распределения случайного вектора (^₍,…, Плотность распределения является более удобной (по сравнению с функцией распределения) формой задания непрерывных случайных векторов. Зная плотность распределения по формуле (2.26), можно найти плотность распределения (производная (2.27) существует в точках непрерывности функции f (x…х")).

Плотность распределения случайного вектора обладает следующими свойствами.

Свойство 2.11. Плотность распределения f (x_u …, х") — неотрицательная функция и.

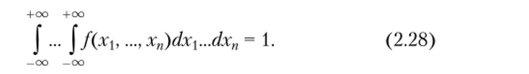
найти функцию распределения и, наоборот, зная функцию распределения, можно по формуле.

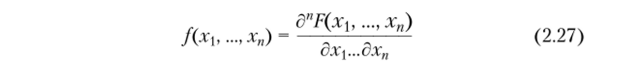
Доказательство. То, что f (?C,…, х") > 0 следует из того, что функция распределения F (xj,…, х") является неубывающей функцией своих аргументов (см. свойство 2.9). Равенство (2.28) следует из определения плотности распределения (2.26), функции распределения (2.27) и свойства 2.4.

Свойство 2.12. Вероятность того, что случайный вектор (?i,…, ?") попадет в квадрируемую область Д равна.

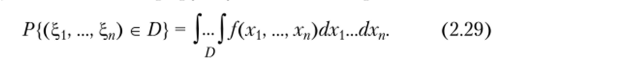
Доказательство. Проведем для двумерного случайного вектора, т. е. для вектора (^₍, ?,₂) ^с плотностью распределения f (x, у) и квадрируемой области на плоскости D.

Найдем сначала вероятность события {х < c,_t < х + Дх, у < ₂ < < у + Ау). На основании формулы (2.24) из 2.2.1 имеем.

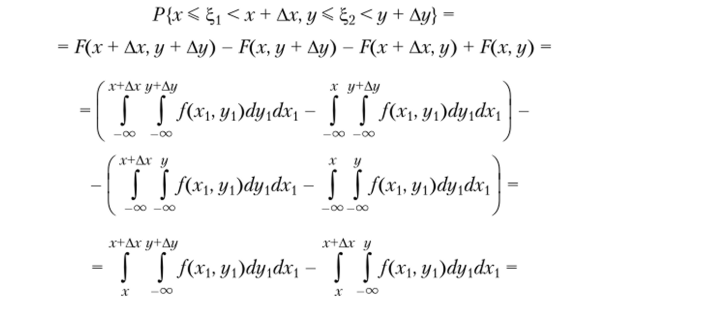
где х < 0j < х + Ах, у < (p_t с у + Ау.

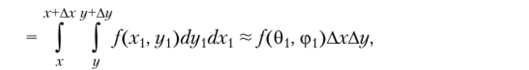
Разобьем плоскость на прямоугольники Ах и Ду прямыми параллельными осям координат (рис. 2.15). Обозначим через К число прямоугольников, целиком попавших в область D.

Рис. 2.15.

События {(?, 1, ?₂) е Д|}, {(^|, ?2) ⁶ Дг}> где ^д1. ^д2 — любые два различных прямоугольника, лежащие в D, несовместны, поэтому вероятность события Р{(%₍, ₂) е D) с учетом равенства (2.24) равна.

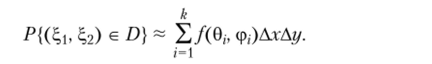
Так как область D квадрируемая, то переходя к пределу при Дг —* 0 и Ау —? 0, получим что и требовалось доказать.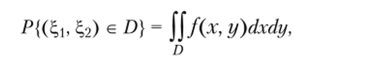

Свойство 2.13. Если f (x_h х₂,…, д") — плотность распределения «-мерного случая вектора (?,],…, ?,»), a f'(x,…, х?) — плотность распределения^{-мерного} случайного вектора (Si…S*), то.

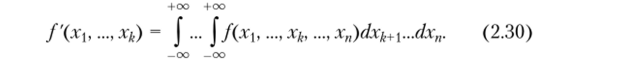
В частности,.

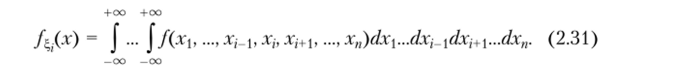
Доказательство. На основании свойства 2.10 и формулы (2.29) функция распределения^{-мерного} случайного вектора (Si…W равна.

Продифференцировав обе части последнего равенства по переменным Х…Хк, получим.

Пример 2.15. Задан двумерный случайный вектор (?], %₂) с плотностью распределения.

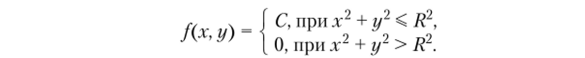
• 1) определить постоянную С;
• 2) найти вероятность события {(?|, Е,₂) е П),

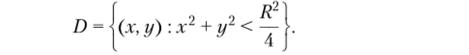
где.

Решение.

1) По свойству 2.11.

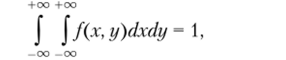
поэтому в нашем случае.

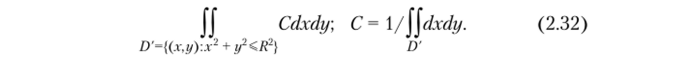
Так как {(дг, у): х² + у² < R²} является кругом с радиусом, равным R, то.

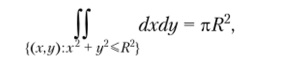
поэтому С = ₂

я/?²

2) По свойству 2.6.

Пример 2.16. Говорят, что случайный вектор (^, %₂) имеет равномерное распределение в квадрируемой области D плоскости, если его плотность распределения равна.

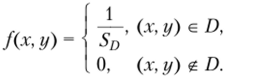
где Sd — площадь области D.

Заметим, что случайный вектор из примера 2.15 имеет равномерное распределение в круге с центром в начале координат и радиусом, равным R.

Пусть D] — квадрируемая область, целиком лежащая в D. Найдем вероятность события {(?₁₍ q₂)? D).

По свойству 2.6 имеем.

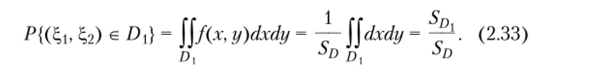
Таким образом, для случайного вектора (%i, <;₂), имеющего равномерное распределение, применим геометрический способ определения вероятностей (см. пример 1.5).

Пример 2.17. Пусть (^_t, $,₂) двумерный случайный вектор с функцией распределения.

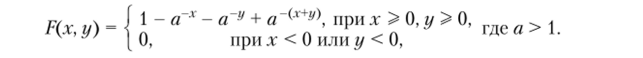
Найти:

• 1) плотность распределения случайного вектора (?i, ?,₂);
• 2) плотность распределения случайной величины с,₂.

Решение. 1. Плотность распределения вероятностей (^ц %₂) на;

ходим по формуле (2.27).

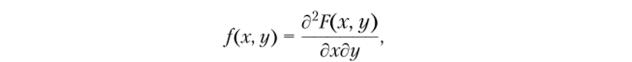
поэтому, если х < 0 или у < 0, то f (x, у) = 0. Пусть, а > 0, у > 0, тогда.

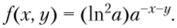
Таким образом.

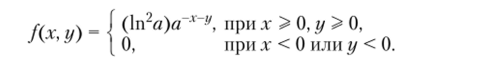
2. Плотность распределения случайной величины ?,₂ находим, но формуле (2.31).

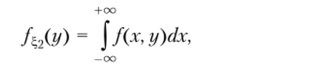
поэтому, если у < 0, то/"., = 0, если же у > 0, то.

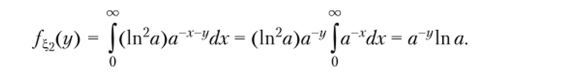
Итак,.

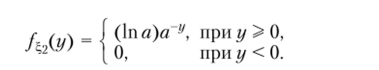
Пример 2.18. Нормальным распределением на плоскости называют распределение двумерного случайного вектора (^_lt с,₂) с плотностью распределения вероятностей.

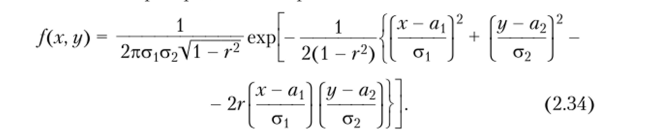
Таким образом, двумерное нормальное распределение определяется пятью параметрами: а, а₂, ст|, ст₂, г.

Найдем плотность распределения случайной величины Согласно свойству 2.13 имеем.

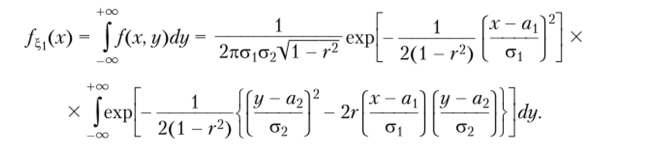
Дополнив выражение, стоящее в фигурных скобках, до полного квадрата, получим.

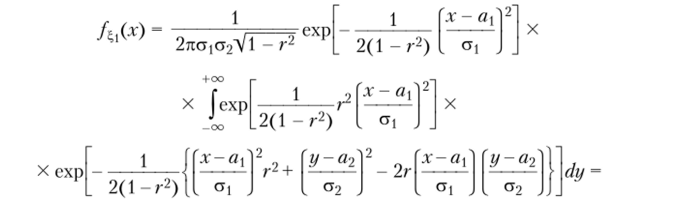
Таким образом, случайная величина имеет нормальное распределение с параметрами а_{} о*. Аналогично можно показать, что случайная величина имеет нормальное распределение с параметрами ^а2²> ^т-^е;

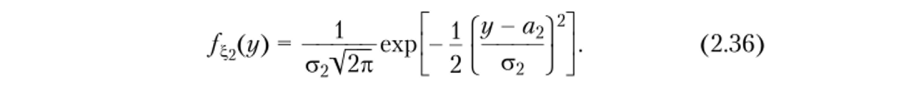
На рис. 2.16 дано графическое изображение плотности нормального распределения на плоскости и плоскостей распределения.

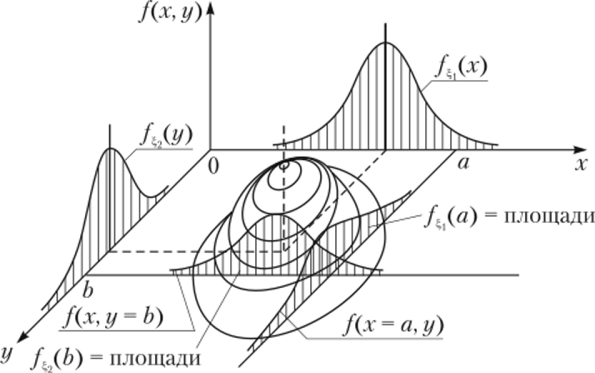
Рис. 2.16.